改进非线性局部平均去噪方法的应用效果

局部平均去噪方法的基本思路是以相点为中心，在相空间内确定一个合适的邻域，然后求取邻域内所有点的均值作为更新值。其中，数值更新直接利用邻域内的点取平均值得到去噪结果，这种过分简化的线性化处理不能充分刻画混沌序列的非线性动力学特性，会导致较大误差。而且把邻域内各点对去噪后数值的贡献看成是一样的，也不符合噪声特性。

改进的非线性局部平均去噪算法[32]的基本思想是通过在邻域内建立一个加权模型来更新数值，从而校正相空间中点的位置，使其更加逼近真实的吸引子轨迹。即认为相空间一个邻域内的相点符合同一动力学特性，相点更新值可由包括它本身在内的所有邻域点加权得到，如下式：

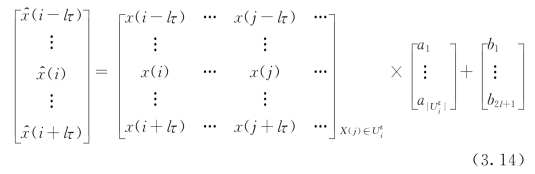
其中，l为邻域半径，a1为X（i）点本身对应的权值，式（3.14）的矩阵形式为：

其中，Φ为邻域点状态矩阵，根据最小二乘原理，向量参数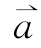，满足：

直接求解式（3.14），容易得到=[1 0…0]T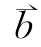，=[0 0…0]，不能达到去噪目的。考虑点X（i）本身应该包含更多的信息，对去噪的贡献最大，其对应权值a1可取接近于1的固定小数值，则式（3.14）转化为

记为

参数估计式为

可由极大似然估计等辨识方法计算得到，也可根据经验选取。将解代入式（3.14），即可得到更新后的相点（i）。

邻域的确定是算法的关键，而初始半径ε的选择又是确定邻域的关键。如果ε太小可能会损失部分有效信息，太大又会使被包含点的动力特性过于复杂，难以用线性方程模拟。本方法按以下步骤确定初始邻域半径ε[32]：

（1）选择半径ε，确定初始邻域Uεi。

（2）计算两点之间的距离如式（3.12），满足distij＜ε的点X（j）∈Uεi，j=1，2，…，N；计算邻域点数|Uεi|，i=1，…，N，标记出所有满足

的点，μ为正整数，根据相空间中点的分布密度确定。

（3）令ε=aε，a＞1，对（2）中标记的点，循环（2）～（3），直到所有点都满足|Uεi|＞μ，记下各点对应的初始半径。

这里，相空间中点的分布密度可通过计算两点之间的平均距离进行估计，方法更具实用性。非线性局部平均去噪方法步骤如下：

（1）重构相空间。选择正整数l，构造2l+1维的嵌入向量X（i）。l需足够大以确保该系统吸引子在重构相空间内没有任何交叠，并且使得嵌入向量包含足够的过去和未来的信息。

（2）确定邻域。初始半径ε的选择应使每一个点的邻域内都包含一定数量的邻域点。(www.xing528.com)

（3）数值更新。取嵌入向量X（i）的中间元素x（i）的更新值为观测点的去噪值，即

式中：（i）为更新值。

（4）减小半径ε，重复（2）～（3），直到找不到邻域点或者更新数值的变化足够小。

局部平均方法在更新数据点时，邻域内的各点被平等看待，如式（3.13）所示。实际上，在邻域中，各点对X（i）的更新值贡献是不同的。改进的非线性局部平均法[11]采用式（3.21）更新数据，aj，bj的加入考虑了不同点的不同贡献，更加符合实际情况。而两点之间的距离计算公式，则沿用式（3.12）所示的∞-范数表达，而常规方法选用的2范数表达为

以二维空间为例，如图3.1所示，式（3.12）给出的是方形域，式（3.22）给出的是属于R2l+1的球形域。二者都是空间R2l+1中的凸集，给出了欧氏空间的通常拓扑，在距离表示方面是等价的。但是式（3.12）的加减计算更为容易，实现更为简单。

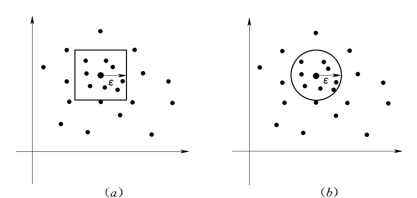
图3.1　邻域点的距离

（a）∞-范数；（b）2范数

式（3.23）为是法国天文学家Henon提出的一种二维映射：

令y（1）=y（2）=0，a=1.4，b=0.3，迭代可得混沌时间序列。任取其中2000个数据点，时间延迟为1，二维相空间图如图3.2（a）所示。图3.2（b）为含有5%噪声水平白噪声的Henon映射时间序列。

图3.2　Henon映射相空间

（a）不带噪声的Henon映射；（b）带5%白噪声的Henon映射

因为Henon映射的关联维数在1和2之间[33]，根据上述讨论，选取参数l=1，即形成3维嵌入向量：

取μ=20，即各点初始邻域中都含有大于20个的邻域点，a1=0.6，是观测点本身的权值。应用改进的局部平均法进行去噪处理的结果如图3.3所示。可以看出，由于对邻域中的相空间点赋予了不同的权值，区别对待各点对数据更新的贡献，使得包含真实数据的信息能够突出显示，改进的局部平均法对邻近轨迹的分辨能力较好。

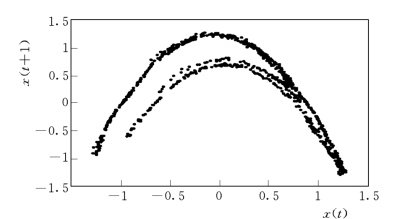
图3.3　Henon映射去噪后的相空间