混沌时间序列预测方法中的嵌入维数确定

一般认为，如果重构相空间的维数足够大，就可以刻画出系统的奇异吸引子，揭示出传统方法无法展示的系统运动规律。所以重构相空间时，通常选取嵌入维数m≥2D+1。常用的计算方法有以下几种：

1.饱和关联维数（G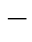P）法

根据关联维数的定义[23]，如果观测序列﹛x（t）﹜中有奇异吸引子存在，那么随着嵌入维数m 的增加，关联指数Dm也会增加。当关联指数Dm增加到一定程度时，得到的饱和值D，即为时间序列﹛x（t）﹜的关联维数。GP法的主要思想是选择不同的领域半径r，分别计算相应的Cn（r），将这些不同的r和Cn（r）代入式（2.41）可拟合出Dm。增加m，求出Dm的饱和值D。根据m≥2D+1，可确定合适的系统嵌入维数m。

2.伪最近邻域法

从几何角度入手，混沌时间序列是高维相空间混沌运动的轨迹在低维空间上的投影。那么在这个投影的过程中[31]，混沌运动轨迹会发生一定的扭曲。原本在高维相空间中并不相邻的两个点，投影在低维相空间时，有可能成为相邻的两点（即伪最近邻点），这也是混沌时间序列无规律的原因所在。重构相空间，其实是从混沌时间序列中构造出混沌运动的轨迹，随着嵌入维数的增大，混沌运动的轨迹将会逐渐展开，伪最近邻点也会被剔除。

m维相空间中，每个相点为X（t）=﹛x（t），x（t+τ），…，x[t+（m—1）τ]﹜，都存在某个距离内最近邻点XF，其距离为Rm（t）=‖X（t）—XF（t）‖。当相空间的维数从m 增加到m+1维时，这两个相点的距离会发生变化，而成为

若Rm+1（t）比Rm（t）有较大变化，则可以认为这是由于高维奇异吸引子中两个相邻的点在投影到低维相空间上时变成伪最近邻点。令

若Sm＞ST，则XF（t）是X（t）的虚假最近邻点，阈值ST可在[10，50]之间选取。

对实测时间序列，从嵌入维数的最小值开始计算伪最近邻点的比值，当增加嵌入维数m到伪最近邻点的比值小于5%或者伪最近邻点不再随着嵌入维数m 的增加而减少时，可以认为奇异吸引子完全展开，此时的m即为最佳嵌入维数。

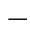综上所述，该方法是一种按固定质量法求取关联维数的方法，其原理与GP法类似，但不同的是：GP法统计半径为r的“筛孔”中所通过的相点对数；而在邻近点维数法中，则固定邻近点个数k，统计k个邻点所占空间的体积 [可用相点X（t）至其第k个邻点间的距离来表示]，通过这种体积与邻点序号k之间存在的关系来计算吸引子维数。这种方法需要考虑如何选择所使用邻点的范围，不能选择靠得太近的邻点，因为这会由于噪声的影响和数据过分集中而使结果扭曲，此时求得的D值偏大，且较多地体现了局域性质；而当k太大时，则无法满足相点概率均匀分布的假定。此外，对于嵌入空间边缘的相点，由于其分布较为稀疏，邻近相点间距较大，对估计的邻近点维数D 有一定影响，但为计算简便起见，建议不考虑边缘相点的影响。

一般说来，当相点分布较为稀疏时，用邻近点维数法比较优越，因为这种方法可以随相点的稀疏变化而自动调整距离尺度，从而使统计出的结果较为可靠；而当相点分布较为密集时，用G-P法较为合理。

3.真实矢量场法

该法又称平滑法或连续性法[32，33]，其实质是：从相空间的几何特性着手，将相空间划分为若干盒子。对于研究系统，如果嵌入参数合适，则轨道充分展开，每个盒中（代表了相空间的某个局域）轨道穿过的方向是相似的（代表了相邻点在短期内的演化特征是相似的），表现出很规则、很光滑的特性；如果嵌入参数不合适，则轨道未充分展开，相互挤压折叠，相轨道穿过每个盒子时方向杂乱，具有很强的随机特征，如图2.7所示。因此可以定义一个方向矢函数或流函数Φ[X（i）]，对每个盒中的轨道方向进行度量：

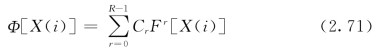
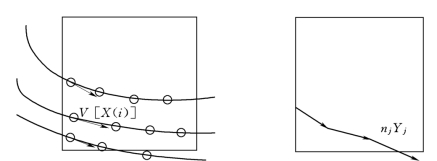
图2.7　方向矢函数示意图

式中：X（i）为对应相空间中第i个相点；R为使用的参考点数；Cr为系数；Fr（·）为任一抽样函数。

如果仅考虑两个参考点，则有

取单位方向矢为

对第j个盒中所有轨道的单位方向矢进行平均(www.xing528.com)

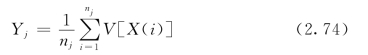
式中：nj为第j个盒中轨道穿过的次数。

令W 为评判重构相空间平滑性的平均方向矢指标，则

式中：N 为所有盒中轨道穿过的次数之和。

显然，如果穿过每个盒的轨道均很规整，或者说光滑性和相似性很好，则各个轨道的单位方向矢V[X（i）]均很接近，每个盒的平均方向矢Yj的模‖Yj‖会很大，即‖Yj‖ ≈1，从而整个相空间的平均方向矢指标W 也很大，W ≈1。对于随机的、杂乱无章的轨道，其单位方向矢V[V（i）]很散乱，则每个盒中平均方向矢Yj的模‖Yj‖会很小，有‖Yj‖ ≈0，从而整个相空间的平均方向矢指标W 很小，W ≈0。根据平均方向矢指标W的这种变化关系，便可评价嵌入参数的好坏，即W 值越大，嵌入空间质量越好。

在真实矢量场计算法中，关键的问题是相空间网格的划分以及方向矢函数的选取。在相空间网格划分中，由于受计算机内存和资料点数的制约，一般对m＜4维的相空间，最大可划分为约30m个网格；m=4维的空间，最大可划分为约20m个网格；而m=5维的空间，最大约可划分为10m个网格。在方向矢函数的选取中，建议选取多种形式的流函数，分别计算出平均方向矢指标W，然后进行综合分析。常常以最大的W 值作为评判指标，通过分析W 值随嵌入维数m 升高而逐渐收敛的程度来确定最优嵌入维数。

GP法和邻近点维数法在应用时都要求预先确定嵌入延迟，而真实矢量场法嵌入延迟是作为可变的参变量，无需确定，这是显著的优点。但是，该法概念复杂，计算较为麻烦，在判断平均方向矢指标随嵌入维数变化是否收敛方面，仅靠目测，缺乏较客观的定量准则，有待改进。

4.Cao方法

Cao方法主要是为了克服在伪最近邻域法中选择阈值的缺点而引入的。则令

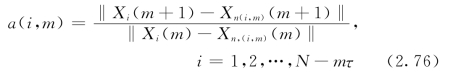
式中：‖·‖为向量的范数，常用的范数为‖Xk（m）—Xl（m）‖=|xk+jτ—xl+jτ|；Xi（m+1）为第i个重构相空间向量，嵌入维数为m+1；Xn（i，m）（m）为按上述范数定义下，离Xi（m+1）最近的向量。其中，n（i，m）为大于等于1且小于等于N—mτ的整数。

如果Xn（i，m）（m）与Xi（m）相等，那么按照范数的定义寻找下一个最近的向量。

定义2.5

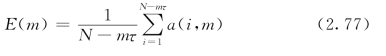
式中：E（m）为所有a（i，m）的均值。

为了检测E（m）的变化情况，令

如果时间序列是由吸引子产生的，当m 大于m0时，E（m）停止变化，那么最小嵌入维数为m0+1。

同时，还可设

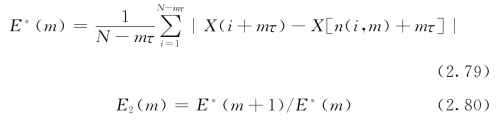
用来辨别确定混沌信号与完全随机信号。