关联维数及其在混沌时间序列预测中的应用

混沌现象最主要的特征是相空间中存在着奇异吸引子，而描述吸引子的基本数学量是它的维数。另外，在进行相空间重构过程中，重构参数——延迟时间τ和嵌入维数m 的选择对重构质量以及后续的分析都有直接影响。因此，吸引子维数计算在混沌分析中起着重要的作用。

奇异吸引子的维数一方面反映了吸引子结构的复杂性，另一方面也反映了吸引子的信息量，因此维数的分析和计算不仅对混沌信号的相空间重构有重要影响，而且也可以用它来刻画吸引子几何结构的特征。对于奇异吸引子，常见的维数主要有：Hausdorff维数、信息维数、Lyapunov维数、关联维数等。Hausdorff维数是这些众多维数定义的基础，它的物理概念明确，有严格的数学定义。但是作为一种纯粹的数学定义，用它对实验数据进行处理时存在很多困难，因此实际很少应用。大多数情况下，决定复杂系统基本运动状态的往往是为数不多的一组变量，它们在高维相空间中组成维数较低的几何对象。但在实验室进行测量时，往往不能跟踪这个低维对象的一切分量，只能将它投影到更低维的平面或直线上来观测，即只能采集一两个变量的数据序列。

那么是否可以在不知道背景相空间维数的情况下，从这少数数据序列中提取关于维数的信息？近年来，从实验数据中计算分维的计算方法得到了发展。Grassberger和Procaccia提出的关联维数算法（简称GP算法）由于特别适用于实验观测数据，且算法简洁易于实现，因此获得了广泛的应用。但是G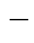P算法也存在一些缺点，如要求数据量很大且数据不含有噪声。而实验数据或多或少都含有噪声，因此利用GP算法得到的关联维数存在较大的误差。下面给出GP算法的详细介绍。

奇异吸引子是轨道在相空间中经过无数次靠拢和分离，来回拉伸和折叠形成的几何结构，具有无穷层次的自相似结构。由于耗散系统运动在相空间的收缩，使奇异吸引子的几何性质，可以通过研究它的空间维数来确定。非线性系统的相空间维数可能很高，而吸引子的维数一般都低于相空间的维数，利用Takens嵌入定理可以将单变量时间序列重构成一个相空间，即只要嵌入维数足够高（一般要求m≥2D+1，D 为吸引子维数），就可以在拓扑等价的意义下恢复原来的动力学特性。GP算法从时间序列计算吸引子关联维数，对实际观测的时间序列x（1），x（2），…，x（t），…，将其用Takens嵌入定理进行时延重构，得到一组空间向量X（t）=﹛x（t），x（t+τ），…，x[t+（m—1）τ]﹜，t=1，2，…，M，其中M=N—（m—1）τ，对于相空间中的这M个点，计算其有关联的向量对数。这里规定凡是距离小于给定正数r的向量，皆称为有关联的向量，向量的距离一般有两种表示方法，2范数和∞-范数。这里选用∞-范数计算，即以两向量的最大分量差作为距离。2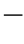范数和∞-范数在计算距离上是等价的，但后者计算量更小一些。计算有关联的向量对数，它在一切可能的M2种配对中所占的比例称为关联积分：

其中，θ（·）为Heaviside单位函数：(www.xing528.com)

根据式（2.35），可计算关联积分Cn（r）。显然计算结果与r的取值有关。如果r过大，导致所有点对的距离rij都小于r，则Cn（r）=1；如果r过小，则所有rij都大于r，Cn（r）=0。两种情况都不能反映系统的内部性质，没有意义，应根据情况适当选取r。当r→0时关联积分Cn（r）与r存在以下关系：

其中，D是关联维数，恰当地选取r，使得D能够描述奇异吸引子的自相似结构，由上式可得

在实际数值计算中，通常给定一些具体的r（r充分小），如果r取得太小已经低于环境噪声和测量误差造成的矢量差别，那么式（2.41）所得结果不是关联维数而是嵌入维数。通常的做法是让嵌入维数从小到大的增加，对每个嵌入维数取双对数关系logCn（r）～logr中的直线段，用最小二乘法进行拟合，得出一条最佳直线，该直线的斜率称为关联指数，关联指数会随着嵌入维数的增加而增大，最后到达一饱和值，这个饱和值就是关联维数D，而达到饱和值时的嵌入维数即为能够完全展开吸引子结构的最小嵌入维数。可以看出，关联维数是对相空间中吸引子复杂度的度量，是从实验数据中直接测定的一种维数，较易计算，应用广泛。它的求取有多种意义：一方面，对于随机序列，随着嵌入维数的增加，关联维数也会不断增大。对于混沌序列，随着嵌入维数的增加，关联维数会出现饱和现象。如果始终没有出现饱和现象，那么这个数列是完全随机的，因而可以根据关联维数是否具有饱和现象来区别混沌序列和随机序列；另一方面，关联维数说明描述该系统所需的最少独立变量数为INT（D+1）个，最多（充分）的独立变量数为INT（2D+1）个，INT为取整函数。