混沌时间序列预测方法首次应用于初值敏感性

混沌系统对初始条件非常敏感[4]，系统初态的任何微小误差都将引起系统行为随时间呈指数规律发散，且最终会收敛于状态空间的一个有限区域，即收敛于一个奇异吸引子。这里首先要清楚线性和非线性初值敏感性的区别。

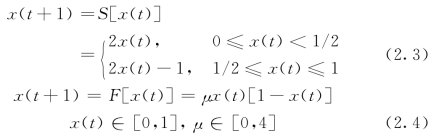
其中，式（2.2）～式（2.4）中x（t）代表当前时刻的状态，式（2.4）中μ代表驱动力与耗散力的相对大小，是系统中的一个参数。在帐篷映射式（2.2）、锯齿映射式（2.3）以及Logistic映射式（2.4）的μ＞μ∞=3.57时都出现了混沌，此时初始条件的细微差别，经过迭代多次后，最终差值无法估计。以Logistic映射为例，取初值分别为x1（0）=0.9000，x2（0）=0.9010的两个有理数进行迭代，所得结果如图2.2所示。

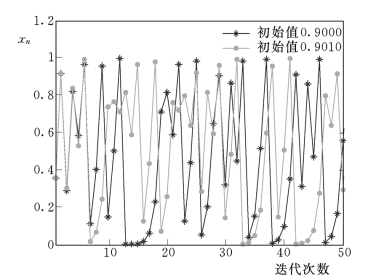
图2.2　Logistic映射迭代50步结果图

可以看出，10步以后两个序列表现出明显的不同，而且已经不存在线性关系，即进入混沌。混沌的这种性质叫做初值敏感性。对如下的线性系统：

其中，x（t）表示系统状态。此系统也对初始条件敏感，当初始条件有一定差值时，最终差值将会导致计算机的溢出。但是对非线性系统例如Logistic映射而言，这种初始条件敏感性不会导致溢出，而是导致不可估计或不可预测的结果。

考虑初值存在差值δx（0）迭代映射t次后变为δx（t），显然有

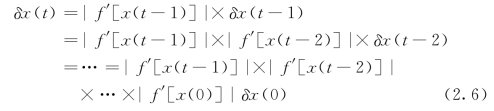
所以

其中

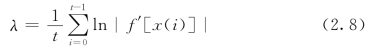(www.xing528.com)

称为Lyapunov指数，是t迭代误差变化的一个平均值，f′（·）代表系统对当前状态的导数。

虽然对稳定的不动点或者其他稳定的周期解，可能在少数几个迭代时存在|f′[x（t）]|＞1，但对全部过程而言，|f′[x（t）]|＜1的迭代次数较多，因而λ＜0。对混沌而言，当t=1，2，…，n时，|f′[x（t）]|均大于1，即λ＞0，所以混沌初始条件敏感性是指λ＞0。即μ较小时，驱动力相对于耗散力比较小，使状态趋向不动点的解和其他周期解。只有当μ＞3.57时，驱动力可以和耗散力进行竞争，此时经过多次伸长与折叠，便产生了混沌。

由上述分析可以看出虽然式（2.4）只是一个简单的迭代函数关系式，但是它包含了状态演化的主要因素，即驱动、耗散和非线性，自然界状态的演化过程并不像直线那样平坦，而是曲折的。驱动因素总要使系统离开原有的状态，而耗散因素总要使系统保持整体结构，力图不使状态演化得太远，非线性相互作用使状态更具有几何、拓扑上的多样性。下面仍用简单的例子，说明自然界状态演化的拓扑形态。

对锯齿映射，可以将x看成角变量，将映射看成是在圆上的映射，x从0到1相当于沿圆周转一圈。映射的前一半，是驱动圆均匀伸长到圆周长为原来两倍，而后一半是将其扭转成8字形，它的上轮和下轮是原来长度的圆，再将上轮折叠下来使两个圆压在一起。

上述的一维映射，反映出状态（点）在x轴上振荡的状况。现在举出二维映射，可以从中看出流动状况。折叠Baker映射

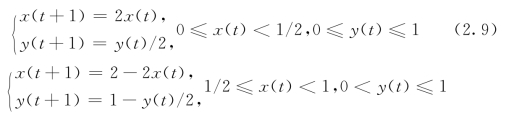
其中，[x（t），y（t）]代表当前时刻系统状态。它将一个方块先压缩伸长，再折叠起来。映射以后，由流动引起的通量相消了。但是对于堆积Baker映射

其中，[x（t），y（t）]代表当前时刻系统状态。与折叠Baker映射的区别是：映射以后，上下两个半块是叠在一起的，显然此时通量加倍了。著名的Smale马蹄映射

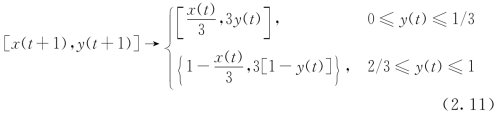
通过伸长和折叠变成了一个马蹄。其中，[x（t），y（t）]代表当前时刻系统状态。除了伸长、折叠、扭转的因子外，物理学上还有剪切因子。如下面是伸长、折叠、剪切三维映射：

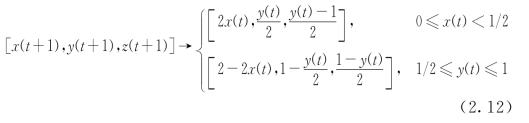
其中，[x（t），y（t）]代表当前时刻系统状态。这一个映射首先是按伸长—折叠Baker映射，然后是剪切映射。

从上述几个简单的分段映射（非线性映射）中可以看出，系统状态演化的主要因子或几何实质是伸长、折叠、扭转和剪切。