自测题一
(一)判断题:每小题2分,共20分(判断下列各题是否正确,正确的在题后面的括号内画“√”号,错误的画“×”号)。
1.设S 是奇数的集合,则S 关于数的乘法构成半群。( )
2.设S 是4的所有整数倍数集合,则S 关于数的乘法是交换半群。( )
3.设G 是实数域R上的所有n 阶对角阵做成的集合,则G 关于矩阵的乘法是群。( )
4.有理数集合Q,关于数的乘法构成群。( )
5.设S 是群G 的非空子集,如果对任意x,y∈S,都有xy∈S,并且x-1∈S,则S 是G 是子群。( )
6.设G 是非交换群,则对任意a,b∈G,都有(ab)3=a3b3。( )
7.全体正有理数集合Q+关于乘法是群。( )
8.设G 是群,a∈G,则a 的逆元的唯一的。( )
9.以4为模的剩余类加群(Z4;+)不是循环群。( )
10.设a 是群G 中的任一元素,a 的阶为n,则a 生成循环群为H 为( )
H={a0=e,a,a2,…,an-1}
(二)单项选择题:每小题2分,共12分(从每小题给出的四个备选答案中,选出一个正确答案,并将正确答案的号码写在题后面的括号内)。
1.设G 是群,a∈G,a 的阶为无穷,k,l是两个整数、当k≠l时,则( )。
A.ak≠al
B.当k 是l的倍数时,有ak=al
C.仅当k 与l不互质时,有ak≠al
D.上述情况均不一定
2.设H1,H2 都是G 的子群,e1,e2,e 分别是H1,H2,G 的单位元,则( )。
A.e1=e2=e B.e1≠e2
C.e1=e2≠e D.e1,e2,e 互不相同
3.设S 是齐次线性方程组
的解向量的集合,关于n 元向量的加法,则S( )。
A.不是群 B.是交换群
C.是循环群D.是非交换群
4.设S 是用4除余数是1的所有整数的集合,即
S={m ∈Z|m=4q+1,q ∈Z}
关于数的乘法,则S 是( )。
A.群 B.无单位元的半群
C.单位元的半群 D.既不是群,也不是半群
5.在剩余类加群(Z6;+)中,3的阶是( )。
A.2B.3C.4D.6
6.剩余类加群(Z8;+)的如下的4个子集,关于剩余类加法是(Z8;+)的子群的有( )。
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(三)求出以6为模的剩余类加群(Z6;+)中每个元素的阶,并找出它的一个2阶子群。(10分)
(四)设n 为任一自然数,nZ表示n 的一切整数倍组成的集合,即
nZ={nl|l=0,±1,±2,…}
证明:(nZ;+)是整数加群的子群。(10分)
(五)设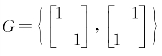 ,
,
证明:G 关于矩阵乘法是循环群。(10分)
(六)设G={1,-1,i,-i},则G 关于数的乘法是群。(8分)
(七)设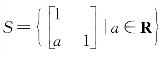 ,
,
证明:S 关于矩阵乘法是M2(R)的子群。(10分)
(八)指出置换群(S3;·)的各元素的阶,并且找出S3 的所有2阶子群。(10分)
(九)设G 是群,a∈G,证明a 与a-1 有相同的阶。(10分)
自测题二
(一)判断题:每小题2分,共20分(判断下列各题是否正确,正确的在题后面的括号内画“√”号,错误的画“×”号)。
1.设S 是3的所有整数倍数的集合,则S 关于数的加法是交换半群。( )
2.设G={1,-1},则G 关于数的乘法是群。( )
3.设e 是群G 的单位元,a∈G,若am=e,则m 是a 的阶。( )
4.设G 是群,则G 中的消去律成立,即对任意a,b,c∈G,若ab=ac,则b=c,若ba=ca,则b=c。( )
5.设G 是半群,如果G 有单位元,则G 一定是群。( )
6.设R 表示非零实数组成的集合,则R 关于数的乘法运算是群。( )
7.设e 是群G 的单位元,则e 必在G 的任一子群中,并且e 也是G 的任一子群的单位元群。( )
8.整数加群不是循环群。( )
9.用N 表示自然数的全体构成的集合,则N 关于数的乘法不是半群。( )
10.设H 是群G 的子群,a∈H,则a 在H 中的逆元就是a 在G 中的逆元。( )
(二)单项选择题:每题2分,共12分(从每小题给出的四个备选答案中,选出一个正确答案,并将正确答案的号码写在题后面的括号内)。
1.设S 是非负整数集,则S 关于数的乘法( )。
A.是群
B.是有单位元的半群
C.是无单位元的半群
D.不是群,也不是半群
2.剩余类加群(Z8;+)的生成元是( )。
A.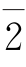 B.
B.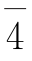 C.
C.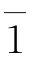 D.没有生成元
D.没有生成元
3.设R为实数域,S=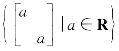 ,则S 关于矩阵乘法是( )。(https://www.xing528.com)
,则S 关于矩阵乘法是( )。(https://www.xing528.com)
A.是群 B.是交换群
C.非可换半群 D.有单位元的可换半群
4.在置换群S3 中,元素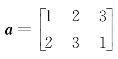 的阶是( )。
的阶是( )。
A.1 B.2C.3 D.4
5.设S={(a1,a2,…,an)|ai∈R},则S 关于n 元向量的加法( )。
A.是非交换群 B.是交换群
C.是循环群 D.是非可换半群
6.M2(R)表示实数域R 上的全体二阶方阵构成的集合,则M2(R)关于矩阵的乘法是( )。
A.无单位元的半群B.有单位元的半群
C.群D.可交换半群
(三)在剩余类加群(Z8;+)中,指出每个元素的逆元。(10分)
(四)设SL2(R)={A∈M2(R)|detA=1}(detA 表示A 的行列式),则SL2(R)关于矩阵的乘法是(M2(R);·)的子群。(10分)
(五)设G 是群,a,b∈G,(1)若aa=ab,则a=b;(2)若aa=a 则a=e。(10分)
(六)设G 是交换群,令
H={a ∈G|a5=e}
证明:H 是G 的子群。(10分)
(七)设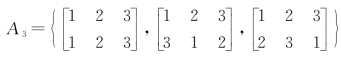 ,
,
证明:A3 关于置换乘法是S3 的子群,并且是循环群。(10分)
(八)设S={A∈M2(R)|AT=A},这里AT 表示A 的转置,则S 关于矩阵的加法是(M2(R);+)的子群。(10分)
(九)设e 是群G 的单位元,a∈G,a 的阶为k,若am=e,则k 整除m。(8分)
【自测题一答案】
(一)判断题
1.√2.√3.×4.×5.√6.×7.√8.√9.×10.√
(二)选择题
1.A2.A 3.B 4.C 5.A6.A
(三)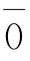 的阶为1;
的阶为1;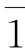 的阶为6;
的阶为6;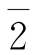 的阶为3;
的阶为3;
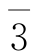 的阶为2;
的阶为2;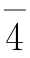 的阶为3;
的阶为3; 的阶为6。
的阶为6。
H=![]() 是(Z6;+)的一个2阶子群。
是(Z6;+)的一个2阶子群。
(四)因为n=n·1∈nZ,故nZ≠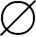 ,对任意nt1,nt2∈nZ,这里t1,t2∈Z,则有
,对任意nt1,nt2∈nZ,这里t1,t2∈Z,则有
nt1+nt2=n(t1+t2)∈nZ
并且nt1 的逆元:-nt1=n(-t1)∈nZ。由子群的充要条件知(nZ;+)是(Z;+)的子群。
(五)设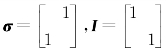 ,G 的运算表如下
,G 的运算表如下
由表中知G 关于矩阵乘法运算封闭,I 是单位元,σ 以自身为逆元,结合律成立,因此,G关于矩阵乘法是群,并且是循环群,σ 是G 的生成元,即(σ)=G={I,σ}。
(六)G 的运算表如下
由运算表知G 关于乘法运算封闭,1是它的单位元,-1的逆元是-1,i的逆元是-i,-i的逆元是i,数的乘法适合结合律,故G 是群,因为
i2=-1,i3=-i,i4=1
因此G=(i)={i0=1,i,i2,i3}是循环群。
(七)对任意![]() ,
,
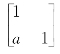 的逆元
的逆元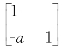 ∈S,故S 是M2(R)的子群。
∈S,故S 是M2(R)的子群。
(八) 的阶为1;
的阶为1; 的阶为2;
的阶为2;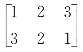 的阶为2;
的阶为2;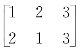 的阶为2;
的阶为2; 的阶为3;
的阶为3;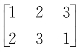 的阶为3。
的阶为3。
2阶子群有:
(九)设a 的阶为k,
(a-1)k=(a-1)kak=(a-1a)k=e
假设有正整数t<k,使(a-1)t=e,那么
at=at·(a-1)t=(a·a-1)t=e
与k 的最小性矛盾,因此a-1 的阶为k。
【自测题二答案】
(一)判断题
1.√2.√3.×4.√5.× 6.√7.√8.×9.× 10.√
(二)单项选择题
1.B2.C 3.D 4.C 5.B 6.B
(三)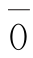 的逆元是
的逆元是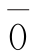 ;
;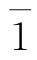 的逆元是
的逆元是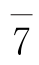 ;
;
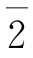 的逆元是
的逆元是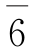 ;
;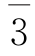 的逆元是
的逆元是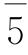 ;
;
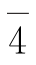 的负元是
的负元是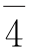 ;
;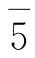 的逆元是
的逆元是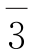 ;
;
 的逆元是
的逆元是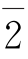 ;
; 的逆元是
的逆元是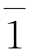 ;
;
(四)因为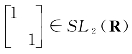 ,故SL2(R)≠
,故SL2(R)≠ ,对任意的A,B∈SL2(R),由det(AB)=detA·detB=1,故AB∈SL2(R),再由detA-1=
,对任意的A,B∈SL2(R),由det(AB)=detA·detB=1,故AB∈SL2(R),再由detA-1=![]() =1,故A-1∈SL2(R),因此SL2(R)是M2(R)的子群。
=1,故A-1∈SL2(R),因此SL2(R)是M2(R)的子群。
(五)(1)因为aa=ab,故a-1aa=a-1ab 得a=b;
(2)由aa=a=ae 及消去律知a=e。
(六)因为e5=e,所以e∈H≠ 。对任意a,b∈H,由(ab)5=a5·b5=e知ab∈H,再由
。对任意a,b∈H,由(ab)5=a5·b5=e知ab∈H,再由
e=(a-1a)5=(a-1)5·(a5)=(a-1)5
知a-1∈H,因此H 是G 的子群。
(七)设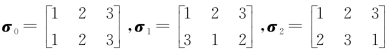 ,列出它们的运算表如下:
,列出它们的运算表如下:
由运算表知A3中任意两个元素乘积还在A3 中,σ0 是单位元,σ1 的逆元是σ2,σ2 的逆元是σ1,因此A3 是S3 的子群。由σ21=σ2,σ31=σ0 知A3=(σ1)={σ01=σ0,σ1,σ21},即A3 是循环群。
(八)零阵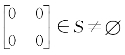 ,对任意A,B∈S,由(A+B)T=AT+BT=A+B,知A+B∈S,又由(-A)T=-A,故-A∈S,因此S 关于矩阵加法是M2(R)的子群。
,对任意A,B∈S,由(A+B)T=AT+BT=A+B,知A+B∈S,又由(-A)T=-A,故-A∈S,因此S 关于矩阵加法是M2(R)的子群。
(九)用k 除m 得:m=kq+r,0≤r<k,q∈Z,因此am=(ak)q·ar=ar=e,由k 的最小性知r=0,即k 整除m。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




