自测题答案及离散数学下册

自测题一

（一）填空题。（24分）

1.设A={1，2，3}，B={1，2}，则A∩B=_____，A∪B=_____，A-B=_____，ρ（A）-ρ（B）=_____，ρ（B）×B=_____。

2.设于A 与B 是两个有限集合，则包含排斥定理|A∪B|=_____。

3.设集合A={a，b，c，d}，A 上的关系R={（a，a），（a，c），（b，d），（c，a）}，则R2=_____，MR=_____，MR2=_____，R 的关系图_____，R-1=_____。

4.设R1，R2 是集合A={1，2，3，4}上的二元关系，其中R1={（1，1），（1，2），（2，3）}，R2={（1，4），（2，3），（2，4），（3，2）}，则R1◦R2=_____，R2◦R1=_____，（R2◦R1）-1=_____，R1- 1◦R2- 1=_____。

5.设集合A={a，b，c}，σ 与τ 都是A 上的变换，σ：a→b，b→a，c→c；τ：a→c，b→b，c→b 则τ·σ=_____，σ·τ=_____，σ·σ=_____。

6.设集合A={1，2，3}，A 上的二元关系R 的关系图，如图所示，则关系R 具有的性质是_____。

（二）判断下列命题是否正确。（20分）

1.设A，B 为任意集合，当A=B=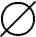时，A-B=B。

2.设X={x，y}，则ρ（X）={，{x}，{y}}。

3.=0。

4.若A∪B=A∪C，则B=C。

5.⊆{a,b,c}。

6.设A={1，2，3，4）}，A 上的关系：

R={(1,1),(2,3),(3,2),(3,4)}

则R 具有对称性。

7.设A={a，b}，A 上的关系R={（a，a），（b，b）}，则R 是A 上的等价关系。

8.在一个由n 个元素组成的集合A 上，空关系基数是0。

（三）多项选择题。（20分）

1.下列命题正确的有_____。

A.{a,b}⊆{a,b,{a,b}}

B.{a,b}∈{a,b,{a,b}}

C.{a,b}⊆{a,{a,b}}

D.{a,b}∈{a,{a,b}}

2.设A={a，b}，下列命题正确的有_____。

A.{a}∈ρ(A)B.{a}⊆ρ(A)

C.{b}∈ρ(A)D.{b}⊆ρ(A)

3.设集合A={a，b，c}，A 上的关系R={（a，b），（a，a），（b，b），（b，a），（c，a）}，则R 具有_____。

A.自反性 B.对称性 C.传递性 D.以上答案都不对

4.设集合A={1，2，3}，R={（1，1），（2，2）}，则R 不具有_____性质。

A.自反性 B.对称性 C.传递性 D.以上答案都不对

（四）计算题。（20分）

1.已知：A={1，2}，求ρ（A）及ρ（A）×A。

2.某班有50名学生，其中8人是足球队员，10人是篮球队员，有3人既是足球队员又是篮球队员，问既不是足球队员又不是篮球队员的学生有几人？

3.设集合A={a，b}，B={1，2}，映射σ：A→B，试列出所有A 到B 的映射σ，并指出哪些是单射、满射和双射？

4.设A={2，4，6，8}，写出A 上的小于等于关系并求出关系图及关系矩阵。

（五）证明题。（16分）

1.设Z为整数集，R={（x，y）|（x-y）/3 是整数，x，y∈Z}，证明R 是A 上的等价关系。

2.设σ：R→R（R为实数集合），σ（r）=2r-10，∀r∈R，求证：σ 是双射。

自测题二

（一）填空题。（28分）

1.设全集E={a，b，c，d，e}，A={a，b，c}，B={a，d，e}，则A∪B=_____，A∩B=_____，A-B=_____，∩=_____，ρ（A）-ρ（B）=_____。

2.设A={x|-1≤x≤2，x∈R}，B={x|0＜x≤5，x∈R}，则A-B=_____，B-A=_____，A×B=_____，B×A=_____。

3.设Z为整数集，R={（x，y）|x，y∈Z，x＞y}，则R 具有_____性。

4.设A={a，b，c，d，e}，A 上的关于等价关系R 的等价类为M1={a，b，c}，M2={d，e}，则等价关系R=_____，关系矩阵MR=_____。

5.设R为实数集，σ（x）=x2-2，τ（x）=x+4，都是R→R 的映射，则τ·σ=_____，σ·τ=_____，τ-1=_____。

6.设R为实数集，σ：R×R→R，σ（x，y）=x+y，则σ 为_____映射，若τ：R×R→R，且τ（xy）=xy，则τ 为_____映射。

7.设集合A={1，2，3}，B={2，3，4}，C={1，2}，R1 是A 到B 上的关系，R2 是B 到C 上的关系，且R1={（a，b）∈A×B|a+b=4}，R2={（b，c）∈B×C|b-c=1}，则R1·R2=_____，MR1·R2=_____，则（R1·R2）-1=_____。

（二）多项选择题。（24分）

1.下列式子正确的有_____。

A.=0 B.∈{a,b} C.⊆{a,b}

2.下列命题正确的是_____。

A.{a}∈{a,b,c} B.{a}⊆{a,b,c}

C.A={a,b},{a}∈ρ(A)D.A={a,b},a⊆ρ(A)

3.设集合A={1，2，3}，A 上关系R 的关系图如图所示，则R 具有_____。

A.自反性，对称性，传递性

B.自反性，传递性

C.对称性，传递性

D.自反性，对称性

4.设R为实数集，映射σ：R→R

σ(x)=-x2-1

则σ 是_____。

A.单射而非满射 B.满射而非单射

C.双射D.即不是单射，也不是满射

5.设A={0，1，2}，R 是A 上的关系，R={（0，1），（0，2），（1，2），（2，2）}，下述结论正确的是_____。

A.R-1={(1,0),(2,0),(2,1)}

B.R-1·R={(0,2)}

C.R·R={(0,2),(1,2)}

D.R·R={(0,2),(1,2),(2,2)}

6.设A 是除0以外的实数集，对A 中的任何两个实数x 和y，我们规定xRy 当且仅当xy＞0，则下列说法正确的有_____。

A.R 自反的 B.R 对称的

C.R 传递的 D.R 是等价关系

（三）计算题。（48分）(www.xing528.com)

1.设A={a，b}，B={1，2，3}，C={1，2}，试求A×（B∩C）和（A×B）∩（A×C），并验证A×（B∩C）=（A×B）∩（A×C）。

2.在一个班级的50名学生中，有26人在第一次考试中得到A，21人在第二次考试中得到A，假如有17人两次考试都没有得到A，试问有多少学生在两次考试中都得到A？

3.下列映射哪些是满射，哪些是单射？ 对每个双射写出它的逆映射。

(1)σ1:N→N,σ1(x)=x2+1,∀x∈N;

(2)σ2:N→N,σ2(x)=x,∀x∈N。

4.若集合A={1，2，3，4，5，6}上的二元关系R1={（a，b）|（a，b）∈A2 且a 整除b}，R2={（a，b）|（a，b）∈A2 且b=2a}，求R1∩R2，R1∪R2，R1-R2。

（四）R 是A 上等价关系，M1，M2，…，Mn 是R 在A 上所有等价类，求证R=M1×M1∪M2×M2∪…∪Mn×Mn。

【自测题一答案】

（一）填空题

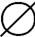1.{1,2},{1,2,3},{3},{{1,3},{2,3},{1,2,3},{3}},{({1},1),({1},2),(,1),(,2),({2},1),({2},2),({1,2},1),({1,2},2)}

2.|A|+|B|-|A∩B|

3.R2={(a,c),(a,a),(c,a),(c,c)}

R-1={(a,a),(c,a),(d,b),(a,c)}

4.{(1,4),(1,3),(2,2)} {(3,3)}

{(4,1),(3,1),(2,2)} {(3,3)}

5.τ·σ:a→b,b→c,c→b;σ·τ:a→c,b→a,c→a;σ·σ:a→a,b→b,c→c。

6.对称性，自反性，传递性。

（二）判断题

1.正确。因为A=B=，故A-B=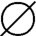，所以A-B=B=。

2.不正确。ρ（A）={，{x}，{y}，{x，y}}。

3.不正确。是没有任何元素的集合，与0概念不一样，0是数字。

4.不正确。设A={1，2，3}，B={1}，C={2}，则A∪B=A∪C=A 但B≠C。

5.正确。因为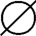是任何集合的子集。

6.不正确。因为（3，4）∈R，但（4，3）∉R。

7.正确。R 具有自反性、对称性、传递性。

8.正确。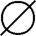无元素，故|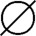|=0。

（三）多项选择题

(1)A、B、D (2)A、C (3)D (4)A

（四）计算题

1.ρ(A)={,{1},{2},{1,2}}

ρ(A)×A={(,1),(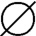,2),({1},1),({1},2),({2},1),({2},2),({1,2},1),({1,2},2)}

2.35

3.σ1:a→1,b→1

σ2:a→2,b→2

σ3:a→1,b→2

σ4:a→2,b→1

σ4、σ4 是双射。

4.R={(2,2),(2,4),(2,6),(2,8),(4,4),(4,6),(4,8),(6,6),(6,8),(8,8)}

（五）证明题

1.证明：① 任意x∈Z，有（x-x）/3是整数，故（x-x）∈R，所以R 具有自性。

② 任意x，y∈Z，若（x，y）∈R，则（x-y）/3是整数，又因为（y-x）/3=-（x-y）/3，故（y-x）/3是整数，所以（y，x）∈R，R 具有对称性。

③ 任意x，y，z∈Z，若（x，y）∈R 且（y，z）∈R，则（x-y）/3和（y-z）/3都是整数，又因为（x-y）/3+（y-z）/3=（x-z）/3，故（x-z）/3是整数，所以（x，z）∈R，R 具有传递性，由以上证明知，R 是Z上的等价关系。

2.证明：任取r1，r2∈R，且r1≠r2，则σ（r1）-σ（r2）=2r1-10-（2r2-10）=2（r1-r2）≠0，故σ（r1）≠σ（r2），所以σ 是单射。

又任取y∈R，令2r-10=y，那么r=（y+10）/2∈R，则σ（r）=y，所以σ 是满射，故σ 是双射。

【自测题二答案】

（一）填空题

1.{a,b,c,d,e},{a},{b,c},,{{b},{c},{a,b},{a,c},{b,c},{a,b,c}}

2.{x|-1≤x≤0,x∈R},{x|2＜x≤5}

{(x,y)|-1≤x≤2,0＜y≤5,x,y∈R}

{(x,y)|0＜x≤5,-1≤y≤2,x,y∈R}

3.传递性

4.{(a,a),(b,b),(c,c),(d,d),(e,e),(a,b),(b,a),(a,c),(c,a),(b,c),(c,b),(d,e),(e,d)}

5.x2+2,x2+8x+14,x-4。

6.满射、满射

7.{(2,1),(1,2)},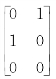,{(1,2),(2,1)}

（二）多项选择题

1.C 2.B、C 3.A、B、C、D 4.D 5.D 6.A、B、C、D

（三）计算题

1.解：A×（B∩C）={（a，1），（a，2），（b，1），（b，2）}，

(A×B)∩(A×C)={(a,1),(a,2),(b,1),(b,2)}

=A×(B∩C)。

2.解：设第一次得A 的学生集合为A，第二次得A 的学生集合为B，|A|=26，|B|=21，故

|A∪B|=(50-17)=33

|A ∩B|=|A|+|B|-|A∪B|=26+21-33=14

答：有14名学生在两次考试中都得到A。

3.（1）σ1 是单射，不是满射；

（2）σ2 是双射，σ2-1（x）=x。

4.解：R1={（1，1），（1，2），（1，3），（1，4），（1，5），（1，6），（2，2），（2，4），（2，6），（3，3），（3，6），（4，4），（5，5），（6，6）}

R2={(1,2),(2,4),(3,6)}

R1∩R2=R2,R1∪R2=R1

R1-R2={(1,1),(1,3),(1,4),(1,5),(1,6),(2,2),(2,6),(3,3),(4,4),(5,5),(6,6)}

（四）证明：对任意的（x，y）∈R，x∈A，y∈A，则存在某个等价类Mi，使x∈Mi，由于（x，y）∈R，故y∈Mi，所以（x，y）∈Mi×Mi⊆ M1×M1∪M2×M2∪…∪Mn×Mn，即R⊆M1×M1。

对任意的（x，y）∈M1×M1∪M2×M2∪…∪Mn×Mn，则必存在某个等价类Mi，使（x，y）∈Mi×Mi，即x，y 同属于一个等价类中，故（x，y）∈R，于是有M1×M1∪M2×M2∪…∪Mn×Mn⊆R，所以R=M1×M1∪M2×M2∪…∪Mn×Mn。