1.用列举法表示下列集合:
(1)1至100的整数中的完全平方数的集合;
(2)大于3而小于等于7的整数集合;
(3)12的质因数集合;
(4)全体偶数的集合。
解:(1){1,4,9,16,25,36,49,64,81,100};
(2){4,5,6,7};
(3){2,3};
(4){…,-2,0,2,…}。
2.用描述法表示下列集合:
(1)被5除余1的整数集合;
(2)平面直角坐标系中单位圆内(不包括单位圆周)的点集;
(3)使![]() 有意义的实数x 的集合。
有意义的实数x 的集合。
解:(1){5x+1|x∈Z};
(2){(x,y)|x2+y2<1};
(3){x|x∈R且x2+x-6≠0}。
3.判定下列各题的正确与错误:
(1){a}∈{a,b,c};
(2){a}⊆{a,b,c};
(3) ∈{a,b,c};
∈{a,b,c};
(4) ⊆{a,b,c};
⊆{a,b,c};
(5){a,b}⊆{a,b,c,{a,b,c}};
(6){a,b}∈{a,b,c,{a,b,c}};
(7){a,b}⊆{a,b,{a,b}};
(8){a,b}∈{a,b,{a,b}};
(9){a,b,c}⊆{a,b,c,{a,b,c}};
(10){a,b,c}∈{a,b,c,{a,b,c}}。
解:(1)错误 (2)正确 (3)错误 (4)正确 (5)正确
(6)错误 (7)正确 (8)正确 (9)正确 (10)正确
4.对于任意集合A,B,C,确定下列各命题是否正确:
(1)如果A∈B 及B⊆C,则A∈C;
(2)如果A∈B 及B⊆C,则A⊆C;
(3)如果A⊆B 及B∈C,则A∈C;
(4)如果A⊆B 及B∈C,则A⊆C;
(5)如果A∈B 及B⊈C,则A∉C;
(6)如果A⊆B 及B∈C,则A∉C。
解:(1)正确。
(2)错误,例如:A={a},B={{a},b},C={{a},b,d},有A∈B,B⊆C,但A⊈C。
(3)错误,例如:A={a},B={a,b},C={{a,b},a},有A⊆B,B∈C,但A∉C。
(4)错误,例如:A={a},B={a,b},C={{a,b},d},有A⊆B,B∈C,但A⊈C。
(5)错误,例如:A={a},B={{a},b},C={{a},d},有A∈B,B⊈C,但A∈C。
(6)错误,例如:A={a},B={a,b},C={{a},{a,b}},有A⊆B,B∈C,但A∈C。
5.写出{a,b,c}的全部子集和真子集,并求幂集。
解:令A={a,b,c},ρ(A)={ ,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}}。ρ(A)中的元素就是A 的全部子集,其中除A 本身之外,都是A 的真子集。
,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}}。ρ(A)中的元素就是A 的全部子集,其中除A 本身之外,都是A 的真子集。
6.求下列集合的幂集:
(1){a,{a}};
(2){ ,a,{a}}。
,a,{a}}。
解:(1)令A={a,{a}},ρ(A)={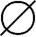 ,{a},{{a}},{a,{a}}};
,{a},{{a}},{a,{a}}};
(2)令B={ ,a,{a}},ρ(B)={
,a,{a}},ρ(B)={ ,{
,{ },{a},{{a}},{
},{a},{{a}},{ ,a},{
,a},{ ,{a}},{a,{a}},{
,{a}},{a,{a}},{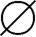 ,a,{a}}}。
,a,{a}}}。
7.设某集合有40个元素,试问:
(1)可构成多少个子集?
(2)其中有多少个子集的基数为奇数?
(3)是否有含有41个元素的子集?
解:(1)可构成240 个子集;
(2)有240/2=239个子集的基数为奇数;
(3)不可能有含有41个元素的子集。
8.设E={1,2,3,4,5},A={1,4},B={1,2,5},C={2,4},试求下列集合:
(1)A∩B;
(2)A∪B;
(3)A∩B∩C;
(4)A∩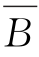 ;
;
(5) ∪
∪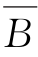 ;
;
(6)(A∩B)∪ ;
;
(7) ;
;
(8)A∪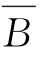 ∪C;
∪C;
(9)ρ(A)∩ρ(B);
(10)ρ(A)-ρ(B)。
解:(1)A∩B={1};
(2)A∪B={1,2,4,5};
(3)A∩B∩C= ;
;
(4)A∩ ={4};
={4};
(5)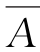 ∪
∪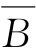 ={2,3,4,5};
={2,3,4,5};
(6)(A∩B)∪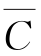 ={1,3,5};
={1,3,5};
(7)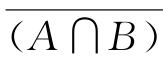 ={2,3,4,5};
={2,3,4,5};
(8)A∪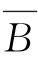 ∪C={1,2,3,4};
∪C={1,2,3,4};
(9)ρ(A)∩ρ(B)={ ,{1}};
,{1}};
(10)ρ(A)-ρ(B)={{4},{1,4}}。
9.判定下列命题哪些是恒成立? 恒不成立? 还是有时成立? 可用文氏图来确定。
(1)若a∈A-B,则a∈A-(A∩B);
(2)若A≠B,则A∩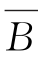 =B∩
=B∩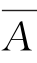 ;
;
(3)(A-B)∪B=A∪B;
(4)(A-B)∪(A-C)=A;
(5)(A-B)∩(A-C)= 。
。
解:(1)恒成立。若a∈A-B,则a∈A,a∉B。由a∉B,有a∉A∩B,所以a∈A-(A∩B)。
(2)恒不成立。由A∩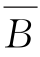 =B∩
=B∩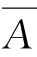 ,必有A=B。
,必有A=B。
(3)恒成立。(A-B)∪B=(A∩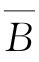 )∪B=(A∪B)∩(
)∪B=(A∪B)∩(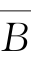 ∪B)=(A∪B)∩E=A∪B。
∪B)=(A∪B)∩E=A∪B。
(4)有时成立。(A-B)∪(A-C)=(A∩ )∪(A∩
)∪(A∩ )=A∩(
)=A∩(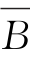 ∪
∪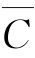 )=A-(B∩C)=A,所以只要A∩B∩C=
)=A-(B∩C)=A,所以只要A∩B∩C=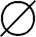 ,等式成立。
,等式成立。
(5)有时成立。当A⊆B∪C 时,成立。
10.A,B 为任意两个集合,求证:
A-(A ∩B)=A-B
11.设A,B,C 是三个任意集合,求证:
(1)(A∪B)-C=(A-C)∪(B-C);
(2)A-(B-C)=(A-B)∪(A∩C)。
12.证明(A∩B)∪(A∩(B∪C))的补集是(A∪B)∩(A∪B)∩(A∪C)。
13.证明下列等式:
(1)(A∪B)∩(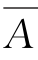 ∪C)=(A∩C)∪(
∪C)=(A∩C)∪( ∩B)∪(B∩C);
∩B)∪(B∩C);
(2)(A∪B)∩(A∪C)=A∪(B∩C)。
(2)(A∪B)∩(A∪C)=A∪(B∩C)。
14.设有集合A,B:
(1)若A-B=B,则A 与B 有什么关系?
(2)若A-B=B-A,则A 与B 有什么关系?
解:(1)若A-B=B,则B=B∩B=(A-B)∩B=A∩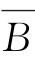 ∩B=A∩
∩B=A∩ =
=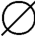 ,又
,又 =B=A-B=A∩
=B=A-B=A∩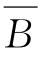 =A∩E=A,所以有A=B=
=A∩E=A,所以有A=B= 。
。
(2)若A-B=B-A,则B∪(B-A)=B∪(A-B),有B=B∪A,同理A∪(B-A)=A∪(A-B),有A=B∪A,所以有A=B。
15.在城镇居民身份调查中,假设在15名居民中,有12名是工人,有5名是干部,其中有3名具有双重身份,即编制是工人,做干部工作(以工代干人员),试问既不是工人又不是干部的非在职人员几人?
解:设A1={工人},A2={干部},则按题意有:
|A1|=12,|A2|=5,|A1∩A2|=3,|A1∪A2|=|A1|+|A2|-|A1∩A2|=14,
所以既不是工人又不是干部的人共15-14=1人。
16.某校足球队有球衣38件,篮球队有球衣15件,棒球队有球衣20件,三个队队员的总数是58人,其中有三人同时参加三个队,试求同时参加两个队的队员共有几人?
解:设A1={足球队员},A2={篮球队员},A3={棒球队员},则按题意有:
|A1|=38,|A2|=15,|A3|=20,|A1∪A2∪A3|=58,|A1∩A2∩A3|=3,
由包含排斥原理,得
|A1∪A2∪A3|=|A1|+|A2|+|A3|-|A1∩A2|-|A2∩A3|-|A1∩A3|+|A1∩A2∩A3|
即58=38+15+20-|A1∩A2|-|A2∩A3|-|A1∩A3|+3。
所以|A1∩A2|+|A2+A3|+|A1∩A3|=18。
参加两个队的队员共18人。
17.(1)在一个班级的50个学生中,有26人在第一次考试中得到A,21人在第二次考试中得到A,假如有17人两次考试都没有得到A,问有多少学生两次考试中都得到A?
(2)在这些学生中,如果第一次考试中得到A 的学生人数等于第二次考试中得到A 的人数,如果仅仅在一次考试中得到A 的学生总数是40,并且有4个学生两次考试都没有得到A,问有多少学生仅在第一次考试中取得A? 问有多少学生仅在第二次考试中取得A? 又问有多少学生在两次考试中都得A?
解:设A1={第一次考试得到A 的学生},A2={第二次考试得到A 的学生}。
(1)按题意有,|A1|=26,|A2|=21,|A1∪A2|=50-17=33,由包含排斥原理,得
|A1∩A2|=|A1|+|A2|-|A1∪A2|=26+21-33=14,
所以两次考试都得到A 的共14人。
(2)|A1|=|A2|,|A1∪A2|=50-4=46。
又|A1∪A2|=|A1∩ |+|A2∩A1|+|A1∩A2|,|A1∩
|+|A2∩A1|+|A1∩A2|,|A1∩ |+|A2∩
|+|A2∩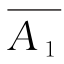 |=40,故|A1∩A2|=46-40=6,由|A1∪A2|=|A1|+|A2|-|A1∩A2|,得到2|A1|=46+6=52,即|A1|=|A2|=26。
|=40,故|A1∩A2|=46-40=6,由|A1∪A2|=|A1|+|A2|-|A1∩A2|,得到2|A1|=46+6=52,即|A1|=|A2|=26。
所以在第一次(或第二次)考试中有26人得到A,在两次考试中都得到A 的有6人。
18.对200名大学一年级的学生进行调查的结果是:其中67人学数学,47人学物理,95人学生物,26人既学数学又学生物,28人既学数学又学物理,27人既学物理又学生物,50人这三门课都不学。
(1)求出对这三门课都学的学生人数;
(2)在文氏图中将正确的学生人数填入其中8个区域。
解:(1)设|A1|={学习数学的学生},|A2|={学习物理的学生},|A3|={学习生物的学生},由题设有,
|A1|=67,|A2|=47,|A3|=95,|A1∩A3|=26,|A1∩A2|=28,|A2∩A3|=27,|A1∪A2∪A3|=200-50=150,由包含排斥原理,得
|A1∪A2∪A3|=|A1|+|A2|+|A3|-|A1∩A3|-|A1∩A2|-|A2∩A3|+|A1∩A2∩A3|,故|A1∩A2∩A3|=150-67-47-95+26+28+27=22,
所以对这三门课都学的学生共22人。
(2)
19.设A={0,1},B={1,2},试确定下面的集合:
(1)A×{1}×B;
(2)A2×B;
(3)(B×A)2;
(4)(A×B)∩(B×A)。
解:(1)A×{1}×B={(0,1,1),(0,1,2),(1,1,1),(1,1,2)}
(2)A2×B={(0,0,1),(0,0,2),(0,1,1),(0,1,2),(1,0,1),(1,0,2),(1,1,1),(1,1,2)}
(3)(B×A)2={((1,0),(1,0)),((1,0),(1,1)),((1,0),(2,0)),((1,0),(2,1)),((1,1),(1,0)),((1,1),(1,1)),((1,1),(2,0)),((1,1),(2,1)),((2,0),(1,0)),((2,0),(1,1)),((2,0),(2,0)),((2,0),(2,1)),((2,1),(1,0)),((2,1),(1,1)),((2,1),(2,0)),((2,1),(2,1))}
(4)(A×B)∩(B×A)= 。
。
20.设A={1,2},构成集合ρ(A)×A。
解:ρ(A)={ ,{1},{2},{1,2}},所以
,{1},{2},{1,2}},所以
ρ(A)×A={(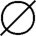 ,1),(
,1),(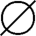 ,2),({1},1),({1},2),({2},1),({2},2),({1,2},1),({1,2},2)}。
,2),({1},1),({1},2),({2},1),({2},2),({1,2},1),({1,2},2)}。
21.设A={a,b},B={1,2,3},C={α,β},试求A×(B∩C)和(A×B)∩(A×C),并验证A×(B∩C)=(A×B)∩(A×C)成立。
解:A×(B∩C)=A×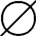 =
= ,
,
(A×B)∩(A×C)={(a,1),(a,2),(a,3),(b,1),(b,2),(b,3)}∩{(a,α),(a,β),(b,α),(b,β)}= ,所以A×(B∩C)=(A×B)∩(A×C)。
,所以A×(B∩C)=(A×B)∩(A×C)。
22.证明:若A×A=B×B,则A=B。
证明:(1)若A=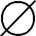 ,则
,则 =A×A=B×B,所以B=
=A×A=B×B,所以B= 。
。
(2)若B=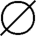 ,同理有A=B=
,同理有A=B= 。
。
(3)若A≠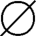 ,B≠
,B≠ ,由A×A=B×B,有A×A⊆B×B,且B×B⊆A×A,由定理1.3.3,故A⊆B 且B⊆A,所以A=B。
,由A×A=B×B,有A×A⊆B×B,且B×B⊆A×A,由定理1.3.3,故A⊆B 且B⊆A,所以A=B。
23.证明:若A×B=A×C,且A≠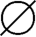 ,则B=C。
,则B=C。
证明:(1)若B= ,则
,则 =A×B=A×C,而A≠
=A×B=A×C,而A≠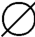 ,所以C=
,所以C= ,即B=C。
,即B=C。
(2)若C=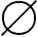 ,同理B=C=
,同理B=C=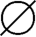 。
。
(3)若B≠ ,C≠
,C≠ ,由A×B=A×C,有A×B⊆A×C 且A×C⊆A×B,由定理1.3.3,故B⊆C 且C⊆B,所以B=C。
,由A×B=A×C,有A×B⊆A×C 且A×C⊆A×B,由定理1.3.3,故B⊆C 且C⊆B,所以B=C。
24.设A,B,C,D 是任意集合,证明(A∩B)×(C∩D)=(A×C)∩(B×D)。
证明:对任意的(x,y)∈(A∩B)×(C∩D),有x∈A∩B,y∈C∩D,即x∈A 且x∈B,y∈C 且y∈D,故x∈A,y∈C 且x∈B,y∈D,有(x,y)∈A×C 且(x,y)∈B×D,(x,y)∈(A×C)∩(B×D),所以(A∩B)×(C∩D)⊆(A×C)∩(B×D)。
对任意的(x,y)∈(A×C)∩(B×D),有(x,y)∈A×C,且(x,y)∈B×D,故x∈A,y∈C 且x∈B,y∈D,即x∈A∩B 且y∈C∩D,有(x,y)∈(A∩B)×(C∩D),因此(A×C)∩(B×D)⊆(A∩B)×(C∩D)。
所以(A∩B)×(C∩D)=(A×C)∩(B×D)。
25.给定正整数集合Z+的下列子集:
A={n|n<12},B={n|n≤8},
C={n|n=2k,k∈Z+},D={n|n=3k,k∈Z+},
F={n|n=2k-1,k∈Z+}。
试用A,B,C,D 和F 表达下列集合:
(1){2,4,6,8};
(2){3,6,9};
(3){10};
(4){n|n 是偶数,n>10};
(5){n|n 是偶数且n≤10,或n 是奇数,且n≥9}。
解:(1){2,4,6,8}=B-F;
(2){3,6,9}=A∩D;
(3){10}=(A-B)-F;
(4){n|n 是偶数,n>10}=C-A;
(5){n|n 是偶数且n≤10,或n 是奇数且n≥9}=(A∩C)∪(F-B)。
26.给定下列自然数集的子集:
A={1,2,7,8};
B={i|i2<50};
C={i|3整除i,0≤i≤30};
D={i|i=2k,k∈Z+,1≤k≤6}。
求下列集合:
(1)A∪(B∪(C∪D));
(2)A∩(B∩(C∩D));
(3)B-(A∪C);
(4)(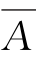 ∩B)∪D。
∩B)∪D。
解:A={1,2,7,8};
B={0,1,2,3,4,5,6,7};
C={0,3,6,9,12,15,18,21,24,27,30};
D={2,4,8,16,32,64}。
则(1)A∪(B∪(C∪D))
=A∪B∪C∪D
={0,1,2,3,4,5,6,7,8,9,12,15,16,18,21,24,27,30,32,64};
(2)A∩(B∩(C∩D))=A∩B∩C∩D=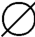 ;
;
(3)A∪C={0,1,2,3,6,7,8,9,12,15,18,21,24,27,30},
B-(A∪C)={4,5}。
(4)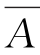 ∩B=B-A={0,3,4,5,6},
∩B=B-A={0,3,4,5,6},
(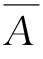 ∩B)∪D={0,2,3,4,5,6,8,16,32,64}。
∩B)∪D={0,2,3,4,5,6,8,16,32,64}。
27.证明:对任意集合A 和B,ρ(A)∩ρ(B)=ρ(A∩B)。(https://www.xing528.com)
证明:对任意x∈ρ(A)∩ρ(B),则x∈ρ(A)且x∈ρ(B),即有x⊆A 且x⊆B,故x⊆A∩B,有x∈ρ(A∩B),所以
ρ(A)∩ρ(B)=ρ(A ∩B)
对任意x∈ρ(A∩B),则x⊆A∩B,有x⊆A 且x⊆B,即x∈ρ(A)且x∈ρ(B),故x∈ρ(A)∩ρ(B),所以
ρ(A ∩B)⊆ρ(A)∩ρ(B)
综上可得:ρ(A)∩ρ(B)=ρ(A∩B)。
28.设A,B 是集合,证明:ρ(A)∪ρ(B)⊆ρ(A∪B),并给出等号成立的充分必要条件。
证明:对任意的x∈ρ(A)∪ρ(B),则x∈ρ(A)或者x∈ρ(B)。
若x∈ρ(A),则x⊆A,而A⊆A∪B,于是x⊆A∪B,故x∈ρ(A∪B)。
同理可证,若x∈ρ(B),则有x∈ρ(A∪B)。
因此ρ(A)∪ρ(B)⊆ρ(A∪B)。
要使等号成立,应有ρ(A∪B)⊆ρ(A)∪ρ(B)。即对任意x∈ρ(A∪B),应有x∈ρ(A)∪ρ(B),于是由x⊆A∪B,能推出x⊆A 或x⊆B,则有A⊆B 或A⊆B。
反之,当B⊆A或A⊆B时,必有ρ(A∪B)⊆ρ(A)∪ρ(B)。
因此,要使ρ(A)∪ρ(B)=ρ(A∪B)成立的充分必要条件是A⊆B 或B⊆A。
29.设x∈B,y∈B,证明{{x},{x,y}}∈ρ(ρ(B))。
证明:由x,y∈B,得{x}∈ρ(B),{x,y}∈ρ(B),故{{x},{x,y}}⊆ρ(B),所以{{x},{x,y}}∈ρ(ρ(B))。
30.设S是任意集合,证明:{ ,{
,{ }}∈ρρρ(S)。
}}∈ρρρ(S)。
证明:因为 ⊆S,所以
⊆S,所以 ∈ρ(S),{
∈ρ(S),{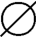 }⊆ρ(S),{
}⊆ρ(S),{ }∈ρρ(S)。又因为
}∈ρρ(S)。又因为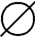 ⊆ρ(S),故
⊆ρ(S),故 ∈ρρ(S),所以{
∈ρρ(S),所以{ ,{
,{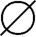 }}⊆ρρ(S),即{
}}⊆ρρ(S),即{ ,{
,{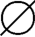 }}∈ρρρ(S)。
}}∈ρρρ(S)。
31.设A,B 是任意集合,若ρ(A)=ρ(B),则A=B。
证明:对任意x∈A,则{x}⊆A,有{x}∈ρ(A),由ρ(A)=ρ(B),故{x}∈ρ(B),即{x}⊆B,得到x∈B,所以A⊆B。
同理可证B⊆A,因此A=B。
32.设A={a},判定下列各题正确与错误:
(1) ∈ρρ(A);
∈ρρ(A);
(2) ⊆ρρ(A);
⊆ρρ(A);
(3){ }⊆ρρ(A);
}⊆ρρ(A);
(4){ }∈ρρ(A);
}∈ρρ(A);
(5){a}∈ρρ(A);
(6){a}⊆ρρ(A)。
解:(1)正确。因为 ⊆ρ(A),故有
⊆ρ(A),故有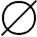 ∈ρρ(A)。
∈ρρ(A)。
(2)正确。空集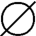 是所有集合的子集。
是所有集合的子集。
(3)正确。因为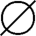 ∈ρρ(A),故有{
∈ρρ(A),故有{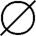 }⊆ρρ(A)。
}⊆ρρ(A)。
(4)正确。因为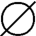 ∈ρ(A),故有{
∈ρ(A),故有{ }∈ρρ(A)。
}∈ρρ(A)。
(5)错误。因为ρ(A)={ ,{a}},ρρ(A)={
,{a}},ρρ(A)={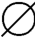 ,{
,{ },{{a}},{
},{{a}},{ ,{a}}}。
,{a}}}。
(6)错误。
33.试求在1到10000之间不能被4,5或6整除的整数的个数。
解:设Ai 是1到10000之间能被i整除的整数的集合,则有:
|A4|=2500,|A5|=2000,|A6|=1666,
|A4∩A5|=500,|A4∩A6|=833,
|A5∩A6|=333,|A4∩A5∩A6|=166,
根据包含排斥原理,有:
|A4∪A5∪A6|=|A4|+|A5|+|A6|-|A4∩A5|-|A5∩A6|-|A4∩A6|+|A4∩A5∩A6|=2500+2000+1666-500-833-333+166=4666,
所以满足题意的整数个数为:10000-4666=5334。
34.设有集合{1,2,…,n},其不重复的一个排列
a1,a2,…,an
满足条件ai≠i(i=1,2,…,n),则称该排列为一个错列。求证集合{1,2,…,n}的错列个数Dn 为
证明:设S 是{1,2,…,n}的所有不重复排列的集合,则|S|=n!。
设有一个排列,如果j 在第j 个位置上,称该排列具有性质Pj,设Aj 是具有性质Pj 的排列的集合,故Aj⊆S。
对于{1,2,…,n}中的任意一个错列,当且仅当这个错列不具有性质P1,P2,…,Pn 中的任意一个性质,所以全部错列组成的集合为:
在集合A1 中,所有排列具有形式1,i2,i3,…,in,其中:i2,i3,…,in 是集合{2,3,…,n}的一个不重复的排列,因而有|A1|=(n-1)!。
同理当1≤j≤n 时,有|Aj|=(n-1)!。
在集合A1∩A2 中的排列具有形式1,2,i3,…,in,其中:i3,i4,…,in是{3,4,…,n}的一个不重复的排列,所以有|A1∩A2|=(n-2)!。
同理当1≤i<j≤n 时,有|Ai∩Aj|=(n-2)!。
一般地,对1≤i1<i2<…<ik≤n,有
|Ai1 ∩Ai2 ∩… ∩Aik|=(n-k)!
集合{1,2,3,…,n}中取k 个元素的组合数是Ckn,故由包含排斥原理:
35.设由某项调查,发现学生阅读杂志的情况如下:
百分之六十阅读甲类杂志;
百分之五十阅读乙类杂志;
百分之五十阅读丙类杂志;
百分之三十阅读甲类杂志与乙类杂志;
百分之三十阅读甲类杂志与丙类杂志;
百分之三十阅读乙类杂志与丙类杂志;
百分之十阅读三类杂志。
试求:(1)确定阅读两类杂志的学生的百分比;
(2)不读任何杂志的学生的百分比。
解:设A1 表示阅读甲类杂志学生的集合;
A2 表示阅读乙类杂志学生的集合;
A3 表示阅读丙类杂志学生的集合。
则按题意有:|A1|=60%,|A2|=50%,|A3|=50%,
|A1∩A2|=30%,|A1∩A3|=30%,
|A2∩A3|=30%,|A1∩A2∩A3|=10%。
(1)|A1∩A2|+|A2∩A3|+|A1∩A3|-3|A1∩A2∩A3|
=30%+30%+30%-3×10%=60%。
(2)|A1∪A2∪A3|
=|A1|+|A2|+|A3|-|A1∩A2|-|A2∩A3|-|A1∩A3|+|A1∩A2∩A3|
=60%+50%+50%-30%-30%-30%+10%
=80%。
所以,|![]() =1-|A1∪A2∪A3|=20%。
=1-|A1∪A2∪A3|=20%。
36.证明:
(1)A∩(B⊕C)=(A∩B)⊕(A∩C);
(2)A∪(B⊕C)=(A∪B)⊕(A∪C)不一定成立。
(2)设A={2,3},B={1,4,7},C={3,5},则B⊕C={1,3,4,5,7},A∪(B⊕C)={1,2,3,4,5,7},A∪B={1,2,3,4,7},A∪C={2,3,5},故有(A∪B)⊕(A∪C)={1,4,5,7},有A∪(B⊕C)≠(A∪B)⊕(A∪C),因此A∪(B⊕C)=(A∪B)⊕(A∪C)不一定成立。
37.设A,B,C 是任意集合,证明:
(1)A-(B∪C)=(A-B)∩(A-C);
(2)A-(B∩C)=(A-B)∪(A-C)。
38.下列各式中哪些成立,哪些不成立,为什么?
(1)(A∪B)×(C∪D)=(A×C)∪(B×D);
(2)(A-B)×(C-D)=(A×C)-(B×D);
(3)(A⊕B)×(C⊕D)=(A×C)⊕(B×D);
(4)(A-B)×C=(A×C)-(B×C);
(5)(A⊕B)×C=(A×C)⊕(B×C)。
解:(1)不成立。
设A={a},B={b},C={c},D={d},有
(A∪B)×(C∪D)={(a,c),(a,d),(b,c),(b,d)},
(A×C)∪(B×D)={(a,c),(b,d)},即
(A∪B)×(C∪D)≠(A×C)∪(B×D)。
(2)不成立。
设A={a,e},B={a,b},C={c,f},D={d),有
(A-B)×(C-D)={(e,c),(e,f)},
(A×C)-(B×D)={(a,c),(a,f),(e,c),(e,f)},即
(A-B)×(C-D)≠(A×C)-(B×D)。
(3)不成立。
设A={a},B={b},C={c},D={d},有
(A⊕B)×(C⊕D)={(a,c),(a,d),(b,c),(b,d)},
(A×C)⊕(B×D)={(a,c),(b,d)},即
(A⊕B)×(C⊕D)≠(A×C)⊕(B×D)。
(4)成立。对任意的(x,y)∈(A-B)×C,有x∈A-B,y∈C,即x∈A,x∉B 且y∈C,因此x∈A,y∈C,且x∉B,y∈C,故(x,y)∈A×C,且(x,y)∉B×C,所以(x,y)∈(A×C)-(B×C),即(A-B)×C⊆(A×C)-(B×C)。
对任意的(x,y)∈(A×C)-(B×C),有(x,y)∈A×C 且 (x,y)∉B×C,故x∈A,y∈C,再由(x,y)∉B×C,得x∉B,所以x∈A-B,y∈C,即(x,y)∈(A-B)×C,有(A×C)-(B×C)⊆(A-B)×C。
综上可得,(A×C)-(B×C)=(A-B)×C。
(5)成立。
(A⊕B)×C=((A-B)∪(B-A))×C
=((A-B)×C)∪((B-A)×C)
=((A×C)-(B×C))∪((B×C)-(A×C))
=(A×C)⊕(B×C)。
39.证明:对任意集合A,B,C,有(A∩B)∪C=A∩(B∪C)当且仅当C⊆A。
证明:必要性,对任意x∈C,有x∈(A∩B)∪C,由(A∩B)∪C=A∩(B∪C),有x∈A∩(B∪C),所以x∈A,即C⊆A。
充分性,若C⊆A,则A∪C=A,所以(A∩B)∪C=(A∪C)∩(B∪C)=A∩(B∪C)。
40.(1)已知A∪B=A∪C,是否必须B=C?
(2)已知A∩B=A∩C,是否必须B=C?
(3)已知A⊕B=A⊕C,是否必须B=C?
解:(1)不一定,例如A={a},B={a,c},C={c},则有A∪B=A∪C,而B≠C。
(2)不一定,例如A={a},B={a,b},C={a,c},则有A∩B=A∩C,而B≠C。
(3)B=C。因为A⊕B=A⊕C,则A⊕(A⊕B)=A⊕(A⊕C),有(A⊕A)⊕B=(A⊕A)⊕C= ⊕B=B=
⊕B=B= ⊕C=C,所以必有B=C。
⊕C=C,所以必有B=C。
41.设A,B,C是任意集合,证明:
(1)(A∪B)∩(B∪C)∩(C∪A)=(A∩B)∪(B∩C)∪(C∩A);
(2)(A∪B)∩(B∪C)∩(C∪A)=(A∩B)∪(B∩C∩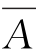 )∪(A∩C∩
)∪(A∩C∩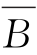 );
);
(3)((A∪B∪C)∩(A∪B))-((A∪(B-C))∩A)=B-A。
证明:(1)(A∪B)∩(B∪C)∩(C∪A)
=((A∩C)∪B)∩(C∪A)
=(A∩C∩(C∪A))∪(B∩(C∪A))
=(A∩C)∪(B∩C)∪(B∩A)
=(A∩B)∪(B∩C)∪(C∩A)。
(3)利用吸收律,得:
42.已知集合A,B,C 满足:
A ∩C ⊆B ∩C,A-C ⊆B-C
证明:A⊆B。
证明:对任意的x∈A,则
(1)若x∈C,则x∈A∩C,而A∩C⊆B∩C,所以x∈B∩C,故x∈B;
(2)若x∉C,则x∈A-C,而A-C⊆B-C,所以x∈B-C,故x∈B。
综上可得,x∈B,所以A⊆B。
43.(1)设A⊆B,C⊆D,那么,一定有A∪C⊆B∪D 吗? 又是否A∩C⊆B∩D 一定成立?
(2)设A⊂B,C⊂D,那么,一定有A∪C⊂B∪D 吗? 又是否A ∩C⊂B ∩D 一定成立?
解:(1)对于任意的x∈A∪C,则x∈A 或x∈C,
若x∈A,而A⊆B,B⊆B∪D,则x∈B∪D,
若x∈C,而C⊆D,D⊆B∪D,则x∈B∪D,
可见,若x∈A∪C,则必有x∈B∪D,因此,A∪C⊆B∪D 一定成立。
易证,A∩C⊆B∩D 也一定成立。
(2)A∪C⊂B∪D 不一定成立。
例如,A={a},C={b},B=D={a,b},显然,A⊂B,C⊂D,而A∪C=B∪D。
所以,一般地,当A⊂B,C⊂D 时,可推出A∪C⊆B∪D。
A∩C⊂B∩D 也不一定成立。
例如,A={a,b},B={a,b,c},C={b,d},D={b,d,e},显然,A⊂B,C⊂D,而A∩C=B∩D。
所以,一般地,当A⊂B,C⊂D 时,可推出A∩C⊆B∩D。
44.设A,B 是集合,证明以下各式中每个关系式彼此等价:
(1)A⊆B, ⊆
⊆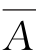 ,A∪B=B,A∩B=A;
,A∪B=B,A∩B=A;
(2)A∩B=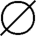 ,A⊆
,A⊆ ,B⊆
,B⊆ ;
;
(3)A=B,A⊕B= 。
。
证明:(1)若A⊆B,对任意的x∈ ,则x∉B,由A ⊆B,有x∉A,x∈
,则x∉B,由A ⊆B,有x∉A,x∈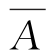 ,所以,
,所以, ⊆
⊆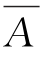 。
。
若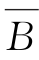 ⊆
⊆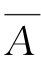 ,对任意的x∈A∪B,则x∈A 或x∈B。如果x∈A,x∉
,对任意的x∈A∪B,则x∈A 或x∈B。如果x∈A,x∉ ,由
,由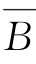 ⊆
⊆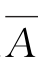 ,得x∉
,得x∉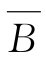 ,x∈B,故A∪B⊆B;如果x∈B,亦有A∪B⊆B。
,x∈B,故A∪B⊆B;如果x∈B,亦有A∪B⊆B。
而B⊆A∪B,所以A∪B=B。
若A∪B=B,对任意的x∈A,因为A⊆A∪B,而A∪B=B,有x∈B,故x∈A∩B。于是A⊆A∩B。又因为A∩B⊆A,所以A∩B=A。
若A∩B=A,因为A∩B⊆B,故A⊆B。
综上可有:A⊆B⇔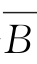 ⊆
⊆ ⇔A∪B=B⇔A∩B=A。
⇔A∪B=B⇔A∩B=A。
(2)若A∩B= ,对任意的x∈A,由A∩B=
,对任意的x∈A,由A∩B= ,可知x∉B,即x∈
,可知x∉B,即x∈ ,所以A⊆
,所以A⊆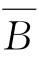 。
。
若A⊆ ,由(1)可得,
,由(1)可得,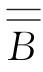 ⊆
⊆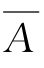 ,即B⊆
,即B⊆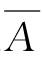 。
。
若B⊆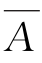 ,假设存在x∈A∩B,则x∈A 且x∈B,由B⊆
,假设存在x∈A∩B,则x∈A 且x∈B,由B⊆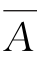 ,得x∈
,得x∈ ,x∉A,与x∈A 矛盾,所以A∩B=
,x∉A,与x∈A 矛盾,所以A∩B=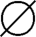 。
。
综上可有:A∩B=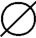 ⇔A⊆
⇔A⊆ ⇔B⊆
⇔B⊆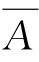 。
。
(3)若A=B,有
若A⊕B=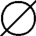 ,因为A⊕A=
,因为A⊕A= ,所以A⊕A=A⊕B,故A=B(参见习题40)。
,所以A⊕A=A⊕B,故A=B(参见习题40)。
综上可有:A=B⇔A⊕B= 。
。
45.设Ai 是实数集合,它被定义为:
证明:![]() 。
。
证明:首先证明![]() 。
。
对任意的![]() ,则必存在某个正整数k,使x∈Ak,即x≤1-
,则必存在某个正整数k,使x∈Ak,即x≤1-![]() ,则x<1,故x∈A0。
,则x<1,故x∈A0。
最后证明![]() 。
。
对任意的x∈A0,即x<1,则存在q>0,使x=1-q,令![]() 表示不超过
表示不超过![]() 的最大整数),则x≤1-
的最大整数),则x≤1-![]() ,即x∈Ak,所以
,即x∈Ak,所以![]() ,故有
,故有![]() 。
。
综上可得,![]() 。
。
46.设Bi 是实数集,它被定义为:
证明:B0=![]() 。
。
证明:先证![]() 。
。
对任意的x∈B0,即x≤1,对任意的i,均有x<1+![]() ,故对任意的i,x∈Bi,所以
,故对任意的i,x∈Bi,所以![]()
再证![]() 。
。
对任意的![]() ,则x∈Bi(i=1,2,…),故对任意的i,都有x<1+
,则x∈Bi(i=1,2,…),故对任意的i,都有x<1+![]() ,则必有x≤1成立。
,则必有x≤1成立。
假设x>1,则存在q>0,使x=1+q,令![]() ,则
,则![]() ,故x∉Bk,与x∈Bi(i=1,2,…)矛盾。因此x≤1,故x∈B0,所以
,故x∉Bk,与x∈Bi(i=1,2,…)矛盾。因此x≤1,故x∈B0,所以![]() 。综上可得,B0=
。综上可得,B0=
47.若A∩B≠ ,求证:
,求证:![]() 。
。
(A∩B)×(A∩B)=(A×A)∩(B×B)=(A×B)∩(B×A)
证明:对任意的(x,y)∈(A∩B)×(A∩B),有x∈A∩B,y∈A∩B,x∈A 且x∈B,y∈A 且y∈B,得x∈A,y∈A 且x∈B,y∈B,于是(x,y)∈A×A 且(x,y)∈B×B,即(x,y)∈(A×A)∩(B×B),所以(A∩B)×(A∩B)⊆(A×A)∩(B×B)。
对任意的(x,y)∈(A×B)∩(B×A),则(x,y)∈A×B,且(x,y)∈B×A,(x,y)∈A,(x,y)∈B,故(x,y)∈A∩B,所以(x,y)∈(A∩B)×(A∩B),故(A×A)∩(B×B)⊆(A∩B)×(A∩B),所以(A∩B)×(A∩B)=(A×A)∩(B×B)。
对任意的(x,y)∈(A∩B)×(A∩B),有x∈A∩B,y∈A×B,x∈A 且x∈B,y∈A 且y∈B,得x∈A,y∈B 且x∈B,y∈A,于是(x,y)∈A×B 且(x,y)∈B×A,即(x,y)∈(A×B)∩(B×A),所以(
A×A)∩(B×B)⊆(A×B)∩(B×A)。
反之,对任意的(x,y)∈(A×A)∩(B×B),有(x,y)∈A×A 且(x,y)∈B×B,故(x,y)∈A 且(x,y)∈B,所以(x,y)∈A∩B,故(x,y)∈(A∩B)×(A∩B),(A×B)∩(B×A)⊆(A∩B)×(A∩B),所以(A∩B)×(A∩B)=(A×B)∩(B×A)。
48.若A∩B≠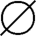 ,求证:
,求证:
(1)(A∪B)×(A∩B)⊆(A×A)∪(B×B);
(2)(A∩B)×(A∪B)⊆(A×A)∪(B×B)。
证明:(1)对任意的(x,y)∈(A∪B)×(A∩B),则x∈A∪B,y∈A∩B,有x∈A 或x∈B,y∈A 且y∈B,得x∈A,y∈A 或x∈B,y∈B,故(x,y)∈A×A 或(x,y)∈B×B,即(x,y)∈(A×A)∪(B×B),所以(A∪B)×(A∩B)⊆(A×A)∪(B×B)。
(2)对任意的(x,y)∈(A∩B)×(A∪B),则x∈A∩B,y∈A∪B,有x∈A 且x∈B,y∈A 或y∈B,得x∈A,y∈A 或x∈B,y∈B,故(x,y)∈A×A 或(x,y)∈B×B,即(x,y)∈(A×A)∪(B×B),所以(A∩B)×(A∪B)⊆(A×A)∪(B×B)。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




