定义3.3.6 设（X，→， 0）是FI代数且∅≠F ⊆X，x∈X且x≠0.如果F满足：
（Fil1）1∈F；
（AFil1）对任意的x，y，z∈X，如果x→（y →z ）∈F且x→y∈F，则z∈F，则称F是X的结合联滤子（associative filter）.由X的全体结合滤子构成的集合记为AFil（X）.
例3.3.6 考虑注3.3.2中所给的FI代数（X，→，0），令F=｛a，b，1｝，则我们可以利用如图3.22所示的Mathematica程序验证F∈AFil（X）.
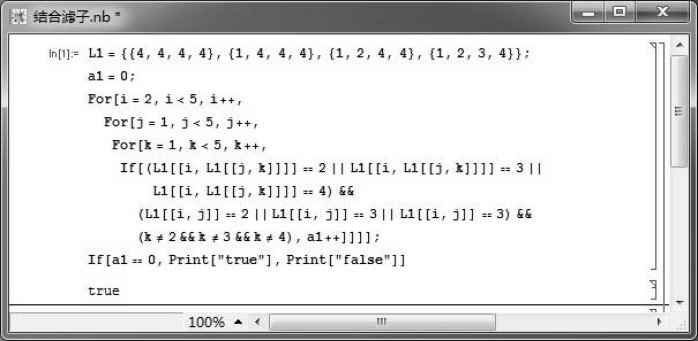
图3.22 验证F∈AFil（X）的Mathematica程序
定理3.3.28 设（X，→， 0）是FI代数，则X的任一结合滤子都是X 的MP滤子.
证明 设F∈AFil（X），则对任意的x，y∈X，设x∈F且x→y∈F，因为由（FI7）得x→（1→y ）=x →y ∈F 且x→1 =1∈F ，所以由（AFil1）y∈F.因此F∈Fil（X）.
定理3.3.29 设（X，→， 0）是FI代数，则X的任一结合滤子都是X的正关联（关联、交换、正则、对合）滤子.
证明 设F∈AFil（X ）且对任意的x， y∈X有（x →y）→x ∈F.因为
(www.xing528.com)
所以由定义3.3.6得x∈F，故由定理3.3.21便得F∈PIFil（X）.再由定理3.3.23、定理3.3.25和定理3.3.26便得F∈CFil（X）、F∈IMFil（X）、F∈RFil（X）和F∈INFil（X）.
注3.3.13 定理3.3.29的逆命题不真，即FI代数的正关联（关联、交换、正则、对合）滤子不必为结合滤子.例如，考虑例3.3.3中所给的FI代数（X，→， 0），令G=｛b，1｝，则可以利用如图3.23所示的Mathematica程序验证G =｛b，1｝∈PIFil（X ），从而由定理3.3.23、定理3.3.25和定理3.3.26便得G∈CFil（X）、G∈IMFil（X）、G∈RFil（X）和G∈INFil（X）.但是G∉AFil（X），事实上，
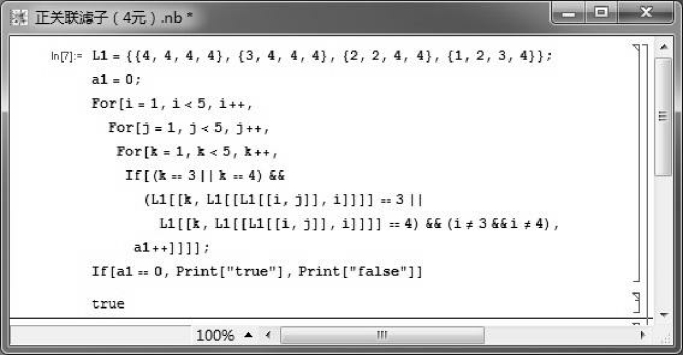
图3.23 验证G =｛b，1｝∈PIFil（X ）的Mathematica程序
定理3.3.30 设（X，→， 0）是FI代数且F∈Fil（X），则F∈AFil（X ）当且仅当F满足：
（AFil2）对任意的x，y，z∈X，x→（y →z ）∈F 当且仅当（x →y）→z ∈F .
证明 必要性：设F∈AFil（X ）.对任意的x，y，z∈X，一方面，设x→（y→z）∈F，因为由（FI1）、（FI10）和（FI3）得
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
