定义3.3.1 设(X,→, 0)是FI代数且∅≠F ⊆X.如果
(INFil1)1∈F;
(INFil2)对任意的x,y∈X,当x∈F且CC (x →y )∈F时都有y∈F,则称F是X的一个对合滤子(involution filter).由FI代数X的全体对合滤子构成的集合记为INFil(X).
注3.3.1 设(X,→, 0)是正则FI代数且∅≠F ⊆X,则由定义3.1.1和定义3.3.1显然可知F∈Fil(X)当且仅当F∈INFil(X).
例3.3.1 设X={0,a, b, c,1},定义X上二元运算“→”如表3.5所示.
表3.5 X上二元运算“→”的定义

可以利用如图3.7所示的Mathematica程序验证(X,→, 0)是一个非正则的FI代数(程序中仅验证条件(FI1)、(FI2)和(FI4),条件(FI3)和(FI5)是显然成立的).
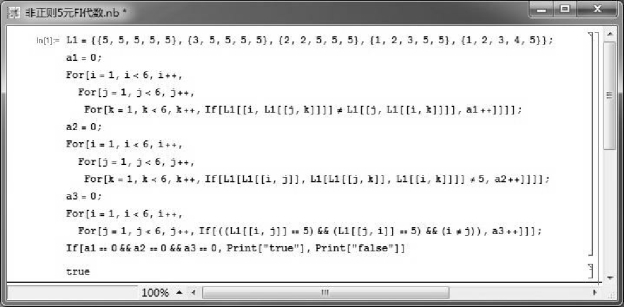
图3.7 验证(X,→, 0)是非正则FI代数的Mathematica程序
令F={c,1},则可利用如图3.8所示的Mathematica程序验证F∈INFil(X ).
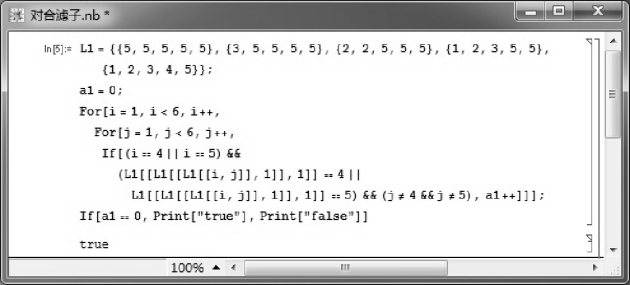
图3.8 验证F∈INFil(X )的Mathematica程序
命题3.3.1 设(X,→, 0)是FI代数且F∈INFil(X),则下列结论成立:
(INFil3)对任意的x,y∈X,当x∈F且x≤y时都有y∈F.
证明 设F∈INFil(X )且对任意x,y∈X有x∈F且x≤y,则x∈F且x→y=1,故由(INFil1)和定理2.2.3中结论(C1)可得CC (x →y )=CC(1)=C(0 )=1∈F ,因此,由x∈F和(INFil2)便得y∈F.(https://www.xing528.com)
定理3.3.1 设(X,→, 0)是FI代数,则X的任一对合滤子都是X的MP滤子.
证明 设F∈INFil(X),则由F满足(INFil1)知F满足(Fil1).对任意的x, y∈X,设x∈F且x→y∈F,由定理2.2.3(C2)得x →y ≤CC (x →y),故由命题3.3.1和x→y∈F得CC (x →y )∈F ,再由(INFil2)和x∈F得y∈F.因此,F∈Fil(X).
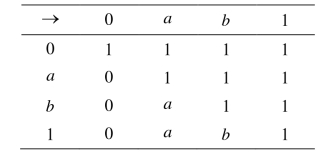
注3.3.2 定理3.3.1的逆命题不真,即X的MP滤子不必是X的对合滤子.例如,设X={0,a,b,1},定义X上二元运算“→”如表3.6所示,则(X,→, 0)是FI代数.
表3.6 X上二元运算“→”的定义
令F={b,1},可用图3.9中的Mathematica程序验证F∈Fil(X).但F∉INFil(X),事实上,b∈F且CC (b →a )=CC (a)=1∈F ,但a∉F.
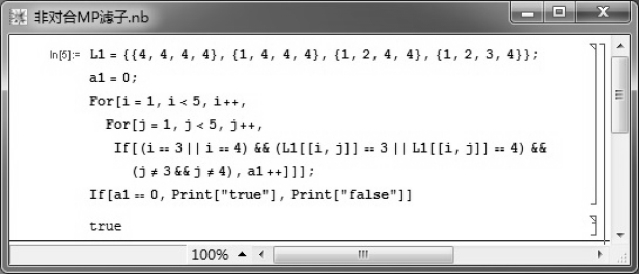
图3.9 验证F∈Fil(X)的Mathematica程序
定理3.3.2 设(X,→, 0)是FI代数且F∈Fil(X),则F∈INFil(X)当且仅当F满足:
(INFil4)对任意的x∈X,如果CC (x)∈F,则x∈F.
证明 必要性:设F∈INFil(X)且对任意的x∈X都有CC (x)∈F,则由(FI7)得
![]()
故由1∈F和(INFil2)便得x∈F,即F满足(INFil4).
充分性:设F∈Fil(X)且满足(INFil4).对任意x,y∈X,设CC (x →y )∈F且x∈F,则由(INFil4)得x∈F且x→y∈F,从而由(Fil2)便得y∈F,因此由定义3.3.1便得F∈INFil(X ).
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




