定义3.1.1[12] 设(X,→, 0)是FI代数且∅≠F ⊆X.如果
(Fil1)1∈F;
(Fil2)对任意的x,y∈X,当x∈F且x→y∈F时都有y∈F,则称F是X的MP滤子(MP-filter).由X的全体MP滤子构成的集合记为Fil(X).
注3.1.1 设(X,→, 0)是FI代数,则由定义3.1.1显然{1}∈Fil(X)且X∈Fil(X).
例3.1.1 设X=[0,1],对任意的x, y∈X,定义X上的蕴涵算子“→”满足:
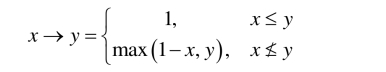
则0→0=1,(X,→, 0)是FI代数且(1/2,1]∈Fil(X),但[1/2,1]∉Fil(X).因为
1/2∈[1/2,1]且1/2 →1/3 =max (1 -1/2,1/3) =max (1/2,1/3) =1/2 ∈[1/2,1],但1/3∉[1/2,1].值得注意的是,对此FI代数(X,→, 0)而言,有如下结论:
![]()
其中,α>1/2且β≥1/2.
例3.1.2 设X={0,a, b,1},定义X上二元运算“→”如表3.1所示,则可以验证(X,→, 0)是一个FI代数.
表3.1 X上二元运算“→”的定义
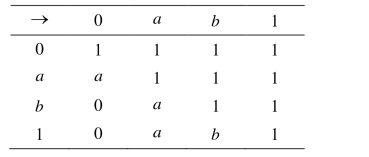
令F={b,1},可利用如图3.1所示的Mathematica程序验证F∈Fil(X).
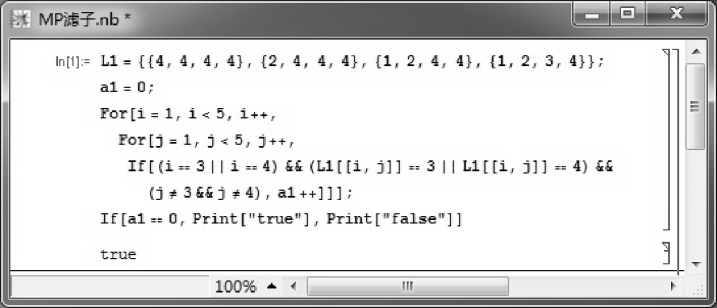
图3.1 验证F∈Fil(X)的Mathematica程序
命题3.1.1 设(X,→, 0)是FI代数且F∈Fil(X),则下列结论成立:
(Fil3)对任意的x,y∈X,当x∈F且x≤y时都有y∈F.
证明 对任意的x, y∈X,设x∈F且x≤y,则由定义2.2.2得x∈F且x→y=1.因为F∈Fil(X),所以由(Fil1)得x∈F且x →y=1∈F ,故由(Fil1)得y∈F.
定理3.1.1 设(X,→, 0)是FI代数且∅≠F ⊆X ,则F∈Fil(X)当且仅当F满足(Fil1)和如下条件(Fil4):
(Fil4)对任意的x,y,z∈X,如果x→y∈F且y→z∈F,则x→z∈F.
证明 充分性:设对任意的x,y,z∈X,F满足(Fil1)和(Fil4),则为证F∈Fil(X),只需证F满足(Fil2).事实上,如果x∈F且x→y∈F,则由(FI6)得1 →x =x ∈F且x→y∈F,从而由(Fil4)便得y=1→y ∈F .因此由定义3.1.1得F∈Fil(X).
必要性:设F∈Fil(X),则F满足(Fil1)和(Fil2).对任意的x,y,z∈X,假设x→y∈F且y→z∈F,因为由(FI2)和(Fil1)得
![]()
所以由x→y∈F和(Fil2)得(y →z)→(x →z )∈F,故由y→z∈F和(Fil2)便得x→z∈F,即F满足(Fil4).定理得证.
定义3.1.2 设(X,→, 0)是FI代数,≤是由→导出的偏序关系且∅≠F ⊆X.如果F关于≤是下定向的上集,即F满足:
(1)对任意的x, y∈X,如果x∈F且y∈F,则存在z∈F使得z≤x且z≤y;
(2)对任意的x, y∈X,如果x∈F且x≤y∈F,则y∈F,则称F是X的偏序滤子(partially ordered filter).(https://www.xing528.com)
例3.1.3 设X=[0,1],对任意的x, y∈X,定义X上的蕴涵算子“→”满足:
![]()
则0→0=1,易证(X,→, 0)是正则FI代数且Fil(X)={{1},X=[0,1]}.注意到由→导出的偏序≤恰是通常的小于等于关系知[1/2,1]是X的偏序滤子,但[1/2,1]∉Fil(X).这表明(正则)FI代数的偏序滤子不必是MP滤子.
定理3.1.2 设(X,→, 0)是正则FI代数,C是X上的伪补算子且∅≠F ⊆X,则F∈Fil(X)当且仅当F是偏序滤子且对任意的x, y∈X满足:


例3.1.4 设X={0,a,b,1},定义X上二元运算“→”如表3.2所示,则可以验证(X,→, 0)是一个FI代数.
表3.2 X上二元运算“→”的定义
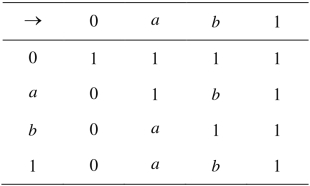
令F={a,b,1},可利用如图3.2所示的Mathematica程序验证F∈Fil(X).但F不是X的偏序滤子,事实上,因为a→b=b且b→a=a,所以a与b不可比较,故对a∈F且b∈F而言,不存在z∈F使得z≤a且z≤b,因此F不是下定向集.这又表明FI代数的MP滤子也不必是偏序滤子.
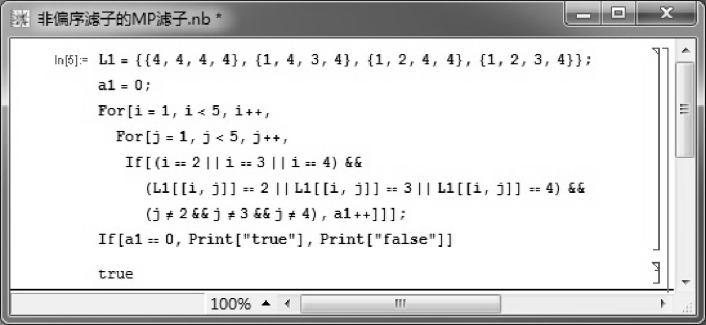
图3.2 验证F∈Fil(X)的Mathematica程序
下面再给出正则FI代数的MP滤子的几个等价刻画:
定理3.1.3设(X,→, 0)是正则FI代数且∅≠F ⊆X ,则F∈Fil(X)当且仅当F满足(Fil1)和如下条件(Fil5):




表3.3 X上二元运算“→”的定义
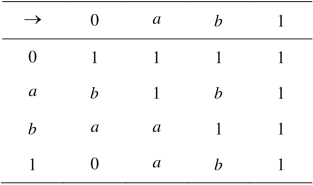
令F1={a,1}且F2={b,1},可利用如图3.3所示的Mathematica程序验证F1∈Fil(X).
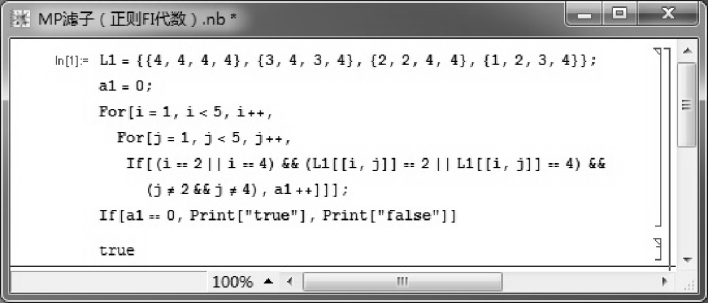
图3.3 验证F1∈Fil(X)的Mathematica程序
由→导出的偏序≤的Hasse图如图3.4所示:
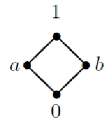
图3.4 (X,→, 0)上由→导出偏序≤的Hasse图

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




