表2.11 X上二元运算“→”的定义
可以利用如图2.10所示的Mathematica程序验证（X，→， 0）是一个CFI代数（程序中仅验证条件（FI1）、（FI2）、（FI4）和（CFI），条件（FI3）和（FI5）是显然成立的）.
图2.10 验证（X，→， 0）是CFI代数的Mathematica程序
定理2.5.11 设（X，→， 0）是CFI代数，≤是→导出的偏序关系且C是X上的伪补算子，则对任意的x∈X都有CC （x）≤x.
证明 因为由（FI6）、（CFI）和（FI13）得
所以由定义2.2.2便得CC （x）≤x.
注2.5.5设（X，→， 0）是CFI代数，则由定理2.2.3中（C2）和定理2.5.11立即可得伪补算子C是一个对合运算，即对任意的x∈X都有CC （x）=x.于是由定义2.3.1立得：
定理2.5.12 CFI代数都是正则FI代数.
注2.5.6 定理2.5.12的逆命题不真，即正则FI代数不必为CFI代数.例如，设X=［0，1］，对任意的x， y∈X，定义X上的蕴涵算子→满足：
则0→0=1，容易验证（X，→， 0）是一个FI代数并且由→导出的偏序关系就是［0，1］上的自然序≤.定义X上的一元运算C：X→X使得∀x ∈X=［0，1］都有C（x）=1-x，则有
故C是X上的伪补算子.易知（X，→， 0）是一个正则FI代数，但不是CFI代数.事实上，取x=0.5，y=0.6，则x， y∈X=［0，1］且x＜y，故x→y=1，从而
然而y→x=max （1 -0.6，0.5 ）=0.5，于是便得（y →x）→x=0.5 →0.5 =1 ≠0.6.这表明（x →y）→y ≠（y →x）→x ，进而（X，→， 0）不是CFI代数.
定理2.5.13 设（X，→， 0）是CFI代数，≤是→导出的偏序关系且C是X上的伪补算子，则（X，≤）构成一个分别以0和1为最小元和最大元的有界格.其中，对任意的x，y∈X，x ∨y =（x →y）→y 且x ∧y =C （（y →x）→C （y ））.
证明 对任意的x， y∈X，因为由（FI11）和（FI12）有
所以（x →y）→y 是x和y的共同上界.设z是x和y的任意一个共同上界，则x≤z且y≤z，从而x→z=1且y→z=1，进而可得
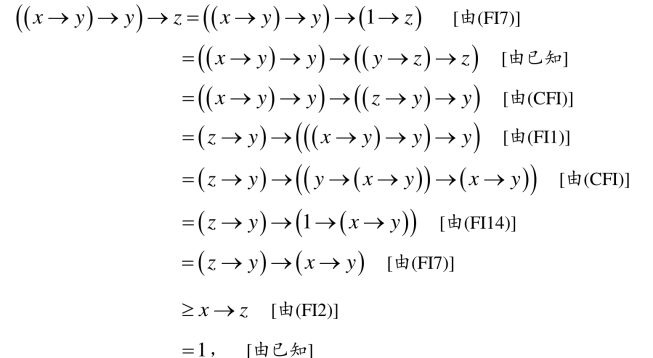
而由（FI6）又得（（x →y）→y）→z≤1，所以（（x →y）→y）→z=1，故由定义2.2.2便得（（x →y）→y ）≤z ，这表明（x →y）→y 是x和y的最小共同上界.因此x和y的上确界x∨y存在且x ∨y =（x →y）→y .
又因为由（FI14）得C （y）→（（y →x）→C （y ））=1，而由（FI1）、定理2.5.12、定理2.3.2和（FI3）得
所以由≤的定义得
故再由CFI代数的正则性和定理2.2.3中（C3）得
这表明C （（y →x）→C （y））是x和y的共同下界.设z是x和y的任意一个共同下界，则z≤x且z≤y，从而再由CFI代数的正则性和定理2.2.3中（C3）得C （x）≤C （z）且C （y）≤C （z），进而C （x）→C （z）=1且C （y）→C （z）=1.于是
而由（FI6）又得z →C （（y →x）→C （y））≤1，所以z →C （（y →x）→C （y））=1，故由≤的定义得z ≤C （（y →x）→C （y ）），这表明C （（y →x）→C （y））是x和y的最大共同下界.因此x和y的下确界x∧y存在且x ∧y =C （（y →x）→C （y ））.
又因为由注2.2.1知0和1分别为偏序集（X，≤）中的最小元和最大元.因此（X，≤）构成一个分别以0和1为最小元和最大元的有界格，且对任意的x， y∈X有
注2.5.7 由定理2.2.3中结论（C3）和注2.5.5知，在CFI代数（X，→， 0）中，伪补算子C是一个逆序对合对应，因此在格（X，≤）中De Morgan对偶律成立，即
定理2.5.14 设（X，→， 0）是CFI代数，则对任意的x∈X，下列各条成立：
（1）（x →y）→（x →z）=（x ∧y）→z；
（2）（x →z）→（y →z ）=y→（x ∨z）；
（3）x →y ≤（x ∨z）→（y ∨z）；
（4）x→（y ∨z）=（x →y）∨（x →z）；（5）（x ∧y）→z =（x →z）∨（y →z）；
（6）x→（x ∧y ）=x →y；
（7）（x ∨y）→y =x →y ；
（8）（x →y）∨（y →x）=1；（9）x →y ≤（x ∧z）→（y ∧z）.
证明 （1）因为
所以（1）成立.
（2）由（FI1）和定理2.5.13得
（3）因为由定理2.5.13和（FI2）得
所以由（FI6）得（x →y）→（（x ∨z）→（y ∨z ））=1，因此x →y ≤（x ∨z）→（y ∨z）.
（4）一方面，因为y≤y∨z且z≤y∨z，所以由（FI8）得
于是x→（y ∨z）≥（x →y）∨（x →z），故（（x →y）∨（x →z））→（x→（y ∨z））=1.
另一方面，由上面已证不等式得
所以由（FI6）又得（x→（y ∨z））→（（x →y）∨（x →z ））=1.因此由（FI4）便得
（5）由正则性、已证结论（4）和De Morgan对偶律得
（6）由定理2.5.13和正则性得
（7）由定理2.5.13和（FI13）得
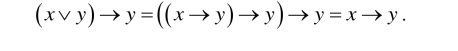
（8）因为
所以（8）成立.
（9）因为
所以由（FI6）得（x →y）→（（x ∧z）→（y ∧z ））=1，因此由≤的定义便得
定理2.5.15 设（X，→， 0）是CFI代数，≤是→导出的偏序关系且C是X上的伪补算子.则（X，≤）是一个分别以0和1为最小元和最大元有界分配格.其中，对任意的x，y∈X，x ∨y =（x →y）→y 且x ∧y =C （（y →x）→C （y ））.
证明 由定理2.5.13和注1.3.5知，为了完成定理的证明，只需证明：对任意的x，y，z∈X，x ∧（y ∨z）=（x ∧y）∨（x ∧z ），又因为x ∧（y ∨z）≥（x ∧y）∨（x ∧z）显然成立，所以只需证明x ∧（y ∨z）≤（x ∧y）∨（x ∧z ）即可.事实上，由定理2.5.14中结论（4）和（9）得
再由（FI6）便得（x ∧（y ∨z））→（（x ∧y）∨（x ∧z ））=1，故再由≤的定义便得
因此（X，≤）是一个有界分配格.
下面我们给出CFI代数的几个等价表示定理：
定义2.5.5 称（2， 0）型代数（X，→， 0）为NFI代数，如果对任意的x，y∈X满足：
（NFI1）0→x=1；
（NFI2）（x →0）→0=x；
（NFI3）x →y =（y→0）→（x→0）；
（NFI4）（x →y）→（x →z）=（y →x）→（y →z）.其中，1=0→0.
定理2.5.16 CFI代数都是NFI代数.
证明 设（X，→， 0）是CFI代数，由定义2.5.4、定理2.5.11和定理2.3.2可知（X，→， 0）满足（NFI1）—（NFI3）.下证（NFI4）成立.事实上，对任意的x，y，z∈X，因为
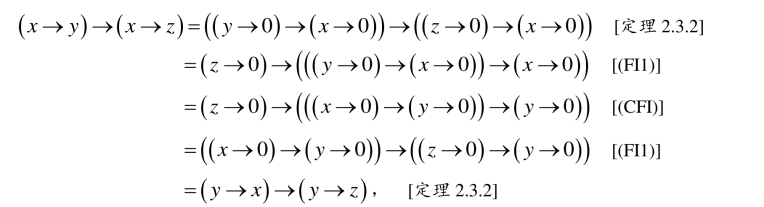
所以（X，→， 0）满足（NFI4）.因此CFI代数都是NFI代数.
命题2.5.1 设（X，→， 0）是NFI代数，则对任意的x∈X，下列结论成立：
（N1）x→1 =1；
（N2）1→x=x；
（N3）x→x=1.
证明 （1）对任意的x∈X，依次运用（NFI2）、（NFI3）和（NFI1）得
（2）对任意的x∈X，依次运用（NFI2）、（NFI3）和（NFI2）得
（3）对任意的x∈X，依次运用（NFI3）、（NFI4）和（N1）得
命题2.5.2 设（X，→， 0）是NFI代数，则对任意的x，y∈X，下列结论成立：
（N4）x→（y→0）=y→（x→0）；
（N5）（x→0）→y =（y→0）→x .
证明 （1）对任意的x， y∈X，依次由（NFI3）和（NFI2）得
（2）对任意的x，y∈X，依次由（NFI3）和（NFI2）得
命题2.5.3 设（X，→， 0）是NFI代数.则对任意的x， y∈X，下列结论成立：
（N6）（x →y）→y =（y →x）→x；
（N7）如果x→y=1且y→x=1，则x=y.
证明 （1）对任意的x，y∈X有
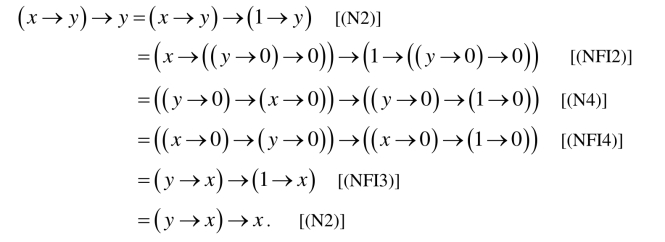
（2）对任意的x， y∈X，设x→y=1且y→x=1，则
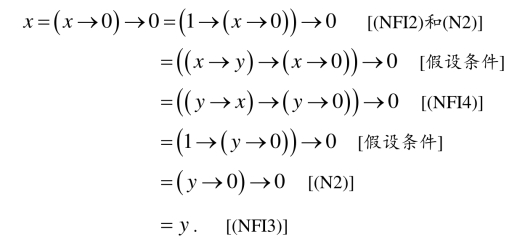
命题2.5.4 设（X，→， 0）是NFI代数，则对任意的x，y，z∈X，下列结论成立：
（N8）如果x→y=1且y→z=1，则x→z=1；
（N9）如果x→y=1，则（y →z）→（x →z）=1且（z →x）→（z →y）=1；
（N10）y→（（x →y）→y）=1且x→（（x →y）→y）=1.
证明 （1）对任意的x，y，z∈X，设x→y=1且y→z=1，则
（2）对任意x，y，z∈X，设x→y=1.一方面由（NFI4）和（N1）有
另一方面，因为由（NFI3）有（y→0）→（x→0）=x →y =1，所以由已证等式又有
（3）对任意x，y，z∈X，因为由（NFI1）有0→（（x →y）→0 ）=1，所以
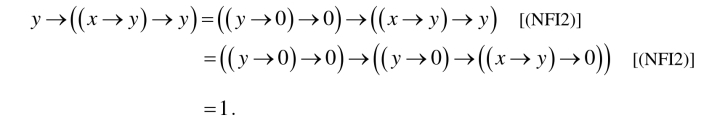
故再由（N6）又得x→（（x →y）→y ）=x→（（y →x）→x）=1.
命题2.5.5 设（X，→， 0）是NFI代数，则对任意的x，y，z∈X，下列结论成立：
（N11）x→（y →z ）=y→（x →z）；
（N12）（x →y）→（（y →z）→（x →z ））=1.
证明 （1）∀x，y，z ∈X，因为由（N10）有x→（（x→（y→0））→（y →0））=1，
所以
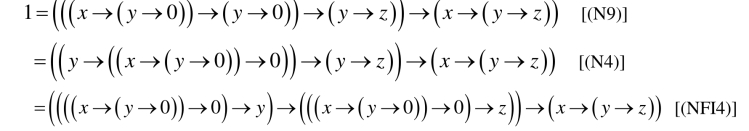
另一方面，由（NFI2）和（NFI3）以及上式又可得
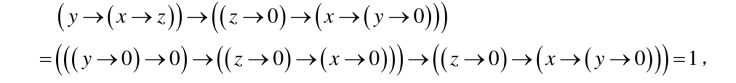(www.xing528.com)
因此由（N8）便得y→（x →z ）=x→（y →z）.
（2）对任意的x，y，z∈X有
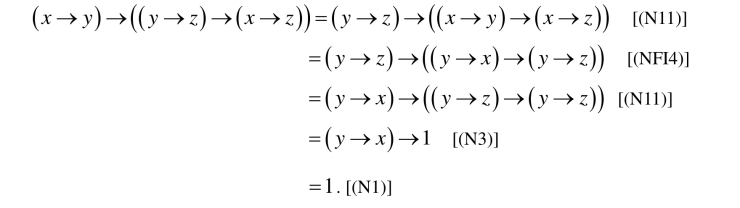
定理2.5.17 NFI代数都是CFI代数.
证明 设（X，→， 0）是NFI代数，由命题2.5.1中（N3）、命题2.5.3中（N6）和（N7）、命题2.5.5中（N11）和（N12）及定义2.5.5中（NFI1）便得（X，→， 0）满足（FI1）—（FI5）和（CFI），因此（X，→， 0）是CFI代数.
推论2.5.1 （2，0）型代数（X，→， 0）是CFI代数当且仅当（X，→， 0）是NFI代数.
定理2.5.18 （2，0）型代数（X，→， 0）是CFI代数当且仅当对任意的x，y，z∈X，下列各条成立：
（NFI-1）1→x=x；
（NFI-2）（x →y）→（（y →z）→（x →z））=1；
（NFI-3）（x →y）→y =（y →x）→x；
（NFI-4）（（x→0）→（y→0））→（y →x）=1.其中，1=0→0.
证明 必要性是显然的.对于充分性，设（X，→， 0）满足（NFI-1）—（NFI-4），由推论2.5.1知只需证明（X，→， 0）是NFI代数，即只需验证（NFI1）—（NFI4）成立即可.下面分12步来完成：
（1）对任意的x∈X，证明x→x=1.依次运用（NFI-1）、（NFI-2）和（NFI2）得
（2）对任意x∈X，证明（x→1）→1 =1.依次运用（NFI-3）、（NFI-1）和（1）得
（3）对任意的x∈X，证明x→1=1.依次运用（NFI-1）、（2）和（NFI-2）得
（4）证明（NFI1），即对任意的x∈X，证明0→x=1.
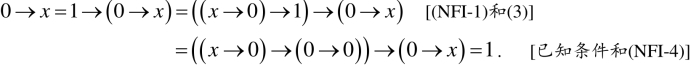
（5）证明（NFI2），即对任意的x∈X，证明（x →0）→0=x.依次运用（NFI-3）、（4）和（NFI-1）得（x →0）→0 =（0→x）→x=1→x =x.
（6）对任意的x， y∈X，证明x →y =y →x=1⇒x =y.
（7）证明（NFI3），即对任意的x， y∈X，证明x →y =（y→0）→（x →0）.一方面，由（NFI4）得（（y→0）→（x→0））→（x →y ）=1.另一方面，又有
综合两方面并结合（6）便得x →y =（y→0）→（x →0）.
（8）对任意的x，y，z∈X，证明x →y =y →z=1⇒x →z=1.
（9）对任意的x，y，z∈X，证明x →y=1⇒（y →z）→（x →z）=1.
（10）对任意的x， y∈X，证明x→（（y →x）→x）=1.
因为由（4）知0→y=1，所以由（9）得（y →x）→（0→x ）=1.因此有
（11）对任意的x，y，z∈X，证明x→（y →z ）=y→（x →z）.
一方面，由（NFI-2）有
另一方面，
综合两方面并结合（8）便得x→（y →z ）=y→（x →z）.
（12）证明（NFI4），即对任意x，y∈X，证明
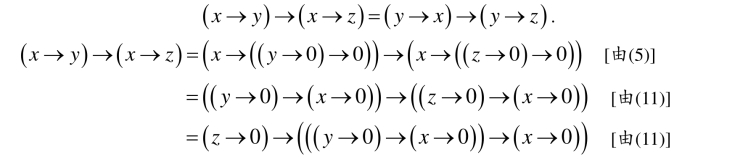
这样就完成了定理的证明.
下面，借助于定理2.5.18再给出CFI代数的一个更简单的表达形式：
定理2.5.19 （2，0）型代数（X，→， 0）是CFI代数当且仅当对任意的x，y，z∈X，下列各条成立：
（NFI-a）0→x=1；
（NFI-b）（y→1）→x =x；
（NFI-c）（y →x）→（z →x）=（x →y）→（z →y）.
其中，1=0→0.
证明 必要性：显然CFI代数满足（NFI-a）和（NFI-b）.又由（FI1）和（FI5）得
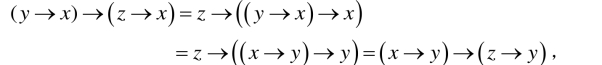
所以CFI代数亦满足条件（NFI-c）.
充分性：由定理2.5.18知只需证明（NFI-1）—（NFI-4）成立.这个过程分如下6步完成：
（1）因为对任意的x∈X，由（NFI-a）得
所以（NFI-1）成立.
（2）对任意的x∈X，证明x→x=1.
（3）对任意的x∈X，证明x→1 =1.事实上，一方面，由（2）得
另一方面，由（NFI-b）又得
综合两方面便得x→1=1.
（4）因为对任意的x∈X，有
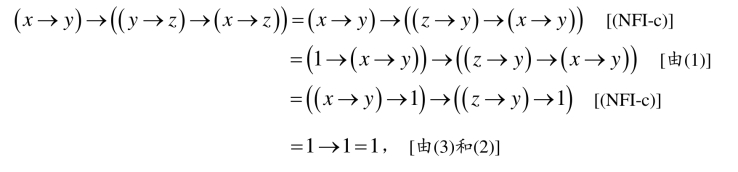
所以（NFI-2）成立.
（5）因为对任意的x，y∈X，有
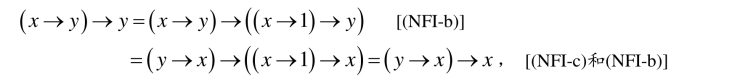
所以（NFI-3）成立.
（6）因为对任意的x，y∈X，有
所以（NFI-4）成立.定理得证.
为了研究命题真知域为一个给定格的逻辑推理系统，1993年，徐扬教授在文献[4]中把格和蕴涵算子相结合提出了（拟）格蕴涵代数的概念，并研究了这一代数的结构特征.目前，格蕴涵代数以及基于格蕴涵代数的格值逻辑理论研究已经获得了巨大的成功.下面，我们讨论CFI代数与格蕴涵代数之间的关系.
定义2.5.6 设（L，∧，∨，'→， 0，1）是一个带有逆序对合对应“'”的有界格，如果对任意的x，y，z∈L，二元运算→：L ×L →L 满足：
（I1）x→（y →z ）=y→（x →z）；
根据定义2.5.6，显然可得：
定理2.5.20格蕴涵代数都是CFI代数.
（1）（L，∧，∨）是分配格；
（2）对任意的x，y∈L，x ∨y =（x →y）→y；
（3）对任意的x，y∈L，x≤y当且仅当x→y=1.
由引理2.5.7和定理2.5.13以及关于CFI代数的讨论，立即可得：
定理2.5.21 设（X，→， 0）是CFI代数，≤是→导出的偏序关系且C是X上的伪补算子，则（X，∧， ∨，C，→，0，1）是一个格蕴涵代数，其中对任意的x，y∈X，
推论2.5.2 格蕴涵代数与CFI代数是等价的代数类.
MV代数理论是与Łukasiewicz逻辑系统相配套的代数理论.为了证明Łukasiewicz逻辑系统的完备性，Chang C.C.于1958年提出了MV代数概念.其原始定义中包含22个条件，现已探明，这些条件很多都不是相互独立的.在MV代数理论的发展过程中，人们在其公理系统简化方面做了大量的研究工作，取得了相当丰硕的成果.MV代数的简化定义之一如下：
定义2.5.7 [13] 称（2，1，2，0）型代数（M，⊕，'→， 0）是MV代数，如果对任意x，y，z∈M，如下条件成立：
（M1）（M，⊕， 0）是以0为单位元的交换半群；
（M2）x⊕x'=0'；
（M3）x⊕0'=0'；
（M4）（x'）'=x；
（M5）x ∨y =y ∨x ；
（M6）x ∨y =y ∨x ；
（M7）（x ∨y ）∨z =x ∨（y ∨x）；
（M8）x⊕（y ∧z）=（x ⊕y）∧（x ⊕z）.
其中，x ∨y =（x '⊕y）'⊕y 且x ∧y =（x '∨y'）'.
进一步，可得MV代数定义的等价形式：
引理2.5.8[13] （2，1，2，0）型代数（M，⊕，'→， 0）是MV代数当且仅当对任意x，y，z∈M，
下列条件成立：
（MV1）（M，⊕， 0）是以0为单位元的交换半群；
（MV2）x⊕0'=0'；
（MV3）（x'）'=x；
（MV4）（x '⊕y）'⊕y =（y '⊕x）'⊕x .
文献[40]指出，格蕴涵代数是与MV代数等价的代数类，从而由推论2.5.2立得：
推论2.5.3 MV代数与CFI代数是等价的代数类.
本节的最后，给出CFI代数与HFI代数之间的关系：
引理2.5.9设（X，→， 0）是正则HFI代数，则对任意的x， y∈X有（x →y）→x =x.证明 一方面，由（FI1）、（FI3）和（FI6）得
另一方面，由正则性和FI代数的性质得
所以由（FI4）便得（x →y）→x =x .
定理2.5.22 正则HFI代数都是CFI代数.
证明 设（X，→， 0）是HFI代数，则由定理2.5.1知（X，→， 0）是FI代数.所以为完成定理的证明，只需证明（CFI）条件成立即可.事实上，由引理2.5.9和定理2.5.2得
因此，定理得证.
注2.5.8 定理2.5.22的逆命题不真，即CFI代数不必为正则HFI代数.例如，设X=［0，1］，对任意的x，y∈X，定义x →y=min （1，1-x +y ），则易验证（X，→， 0）是CFI代数且C（x）=1-x.蕴涵算子→即为Łukasiewicz蕴涵算子，但（X，→， 0）不是正则HFI代数.事实上，取x=0.6，y=0.5和z=0.3，则
从而（x→（y →z））→（（x →y）→（x →z））=1 →0.8 =0.8 ≠1，所以（X，→， 0）不是HFI代数，进而不是正则HFI代数.
定理2.5.23 （2，0）型代数（X，→， 0）是正则HFI代数当且仅当（X，→， 0）是CFI代数且对任意的x， y∈X满足（（x →y）→x）→x=1.
证明 必要性：设（X，→， 0）是正则HFI代数，则由定理2.5.22知（X，→， 0）是CFI代数.而对任意的x， y∈X，由引理2.5.9和（FI3）又得（（x →y）→x）→x =x →x=1.
充分性：设（X，→， 0）是CFI代数且对任意的x，y∈X满足（（x →y）→x）→x=1，则为证（X，→， 0）是正则HFI代数，由定理2.5.12和定义2.5.1可知只需验证（HFI1）、（HFI2）和（HFI3）成立即可.事实上，
（HFI1）：由（FI1）、（FI3）和（FI6）得x→（y →x ）=y→（x →x ）=y→1=y.
（HFI2）：因为由假设条件知（（x →z）→x）→x=1，所以由（CFI）得
于是由定义2.2.2得x→（x →z ）≤x →z，故由（FI8）和（FI10）得
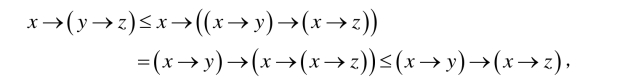
故由定义2.2.2便得（x→（y →z））→（（x →y）→（x →z ））=1.
（HFI3）：设1→x=1，因为由（FI6）得x→1=1，所以由（FI4）得x=1.
注2.5.9 定理2.5.5表明Boole代数与正则HFI代数是等价的，例2.5.3表明Boole代数都是CFI代数，而由注2.5.8又表明CFI代数不是正则HFI代数，由此可见CFI代数不是Boole代数.但是综合2.5.5和定理2.5.23立即可得如下定理.
定理2.5.24 设（X，→， 0）是（2，0）型代数.则下列陈述等价：
（1）（X，→， 0）是正则HFI代数；
（2）（X，→， 0）是Boole代数；
（3）（X，→， 0）是CFI代数且对任意的x，y∈X满足（（x →y）→x）→x=1.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
