定理2.4.16 设（X，→， 0）是正则FI代数，则下列两个结论成立：
（2）对任意的x，y∈X，x和y的上确界sup ｛x，y｝=x∨y存在当且仅当x和y的下确界inf ｛x，y｝=x∧y存在.进一步有x和y的上确界与C （x）和C （y）的下确界互为伪补元.
证明 （1）任取x，y∈X，因为由（FI1）、（FI3）和（FI6）得
反之，类似可证.
证明 因为（X，→， 0）是正则FI代数，所以由定理2.4.17知条件（I）成立当且仅当条件（II）成立，故由假设知（I）和（II）两个条件同时成立.又因为任取x， y∈X，由定理2.4.16知x⊥y是x和y的上界.设z∈X是x和y的任意一个上界，则x≤z且y≤z，从而由定义2.2.2得x→z=1且y→z=1.于是由定理2.3.4和定理2.3.5得
故由定义2.2.2得x⊥y≤z，这表明x⊥y是x和y的上确界，即x ∨y =x ⊥y ，故（X，≤）关于⊥构成并半格.因此由定理2.4.19得（X，≤）构成格.
注2.4.4 设（X，→， 0）是格FI代数.一般来说，（X，→， 0）不必是正则FI代数.例如，设X=［0，1］，→是Gödel蕴涵算子，即对任意的x， y∈X，
证明 对任意的x∈X，由注2.2.1知偏序集（X，≤）中的最小元是0，所以0与x的上确界为x，再由假设可得x=x⊥0，所以由定理2.3.3便得（X，→， 0）是正则FI代数.于是，对任意的x，y∈X，由定理2.4.17又得x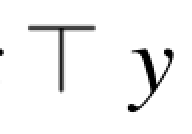
是x和y的下确界.
定理2.4.22设（X，→， 0）是正则的格FI代数，则对任意的x，y，z∈X，下列结论成立：
（1）（x ∨y）→z =（x →z）∧（y →z）；(www.xing528.com)
（2）x→（y ∧z）=（x →y）∧（x →z）.
证明 由定理2.4.1和定理2.4.11立即可得.
定理2.4.23设（X，→， 0）是正则的格FI代数，则对任意的x，y，z∈X，下列结论成立：
（1）（x →y）→（（x ∧z）→（y ∧z））=1；
（2）（x →y）→（（x ∨z）→（y ∨z ））=1.
证明 （1）由定理2.4.6和定理2.4.22中（2）立即可得.
（2）对任意的x，y，z∈X，因为z≤y∨z，所以由定义2.2.2得z→（y ∨z）=1，注意到1是格（X，≤）中的最大元，故由定理2.4.22中（1）便得
又因为y≤y∨z，所以由（FI8）得x →y ≤x→（y ∨z），于是
因此，由定义2.2.2便得（x →y）→（（x ∨z）→（y ∨z ））=1.定理得证.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
