本节的最后,我们通过具体实例来说明吴望名教授给出的Fuzzy蕴涵代数定义中5个条件(FI1)—(FI5)的独立性.


因此,条件(FI2)不能由(FI1)及(FI3)—(FI5)推得.
独立性2.2.3 条件(FI3)不能由(FI1)—(FI2)及(FI4)—(FI5)推得.
例2.2.11 设X={0,a,1},定义X上二元运算“→”如表2.3所示.
表2.3 X上二元运算“→”的定义
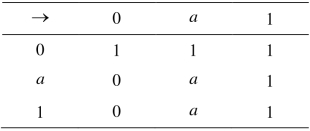
可以利用如图2.2所示的Mathematica程序验证(X,→, 0)满足条件(FI1)、(FI2)和(FI4),且显然满足条件(FI5).
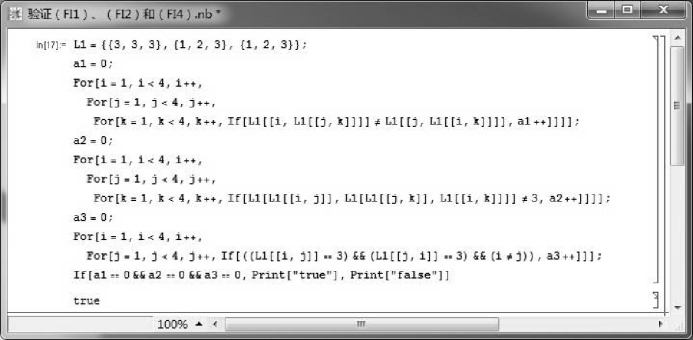
图2.2 验证(X,→, 0)满足条件(FI1)、(FI2)和(FI4)的Mathematica程序
但(X,→, 0)不满足条件(FI3),因为a→a=a≠1.因此,条件(FI3)不能由(FI1)—(FI2)及(FI4)—(FI5)推得.(https://www.xing528.com)
独立性2.2.4 条件(FI4)不能由(FI1)—(FI3)及(FI5)推得.
例2.2.12 设X=[0,1],在其上配备自然偏序关系≤,对任意的x, y∈X,定义x→y=1,则显然(X,→, 0)满足条件(FI1)—(FI3)及(FI5),但不满足条件(FI4).事实上,取x=0.1和y=0.2,则x →y =y →x=1,但x≠y.因此,条件(FI4)不能由(FI1)—(FI3)及(FI5)推得.
独立性2.2.5 条件(FI5)不能由(FI1)—(FI4)推得.
例2.2.13 设X={0,a,1},定义X上二元运算“→”如表2.4所示.
表2.4 X上二元运算“→”的定义
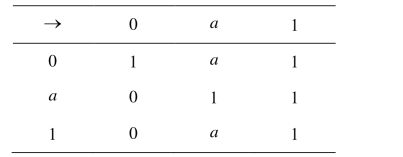
可以利用如图2.3所示的Mathematica程序验证(X,→, 0)满足条件(FI1)、(FI2)和(FI4),且显然满足条件(FI3).
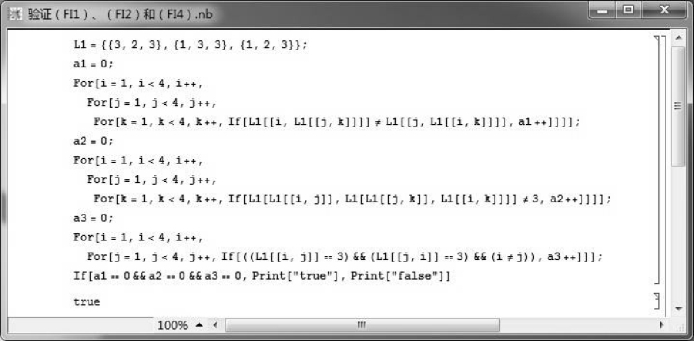
图2.3 验证(X,→, 0)满足条件(FI1)、(FI2)和(FI4)的Mathematica程序
但(X,→, 0)不满足条件(FI5),因为0→a =a≠1.因此,条件(FI5)不能由(FI1)—(FI4)推得.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




