基于对蕴涵算子D-P条件中10条性质和后来添加的3条性质的分析,为了揭示蕴涵算子的共同本质,作为对蕴涵算子代数化研究的一种探索,1990年,吴望名教授提出了Fuzzy蕴涵代数的概念[12].本节我们将具体介绍这一代数结构的定义和基本性质.
定义2.2.1称(2, 0)型代数(X,→, 0)为Fuzzy蕴涵代数(fuzzy implication algebra),简称FI代数(FI-algebra),如果对任意的x,y,z∈X有如下各条成立:
(FI1)x→(y →z )=y→(x →z);
(FI2)(x →y)→((y →z)→(x →z ))=1;
(FI3)x→x=1;
(FI4)如果x →y =y →x=1,则x=y;
(FI5)0→x=1.其中,1=0→0.
例2.2.1设X={0},定义0→0=0(即1=0),则(X,→, 0)是FI代数.此FI代数称为平凡FI代数.
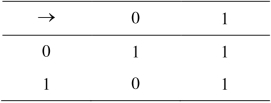
例2.2.2设X={0,1},对任意的x, y∈X,定义x →y=max (1-x, y ),其运算表如表2.1所示,则可以验证(X,→, 0)是FI代数.
表2.1 X上二元运算“→”的定义
例2.2.3设X=[0,1],对任意的x,y∈X,定义x →y=min (1,1-x +y ),则可以验证(X,→, 0)是一个FI代数.蕴涵算子→即为Łukasiewicz蕴涵算子.
例2.2.4设X=[0,1],对任意的x,y∈X,定义x →y=sup{z|min(x, z )≤y },则可以验证(X,→, 0)是FI代数.蕴涵算子→即为Gödel蕴涵算子.
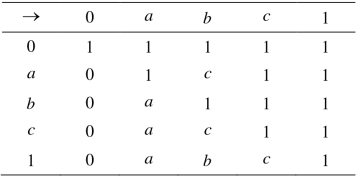
例2.2.5 设X={0,a, b, c,1},定义X上二元运算“→”如表2.2所示.
表2.2 X上二元运算“→”的定义
可以利用如图2.1所示的Mathematica程序验证(X,→, 0)是一个FI代数(程序中仅验证条件(FI1)、(FI2)和(FI4),条件(FI3)和(FI5)是显然成立的).
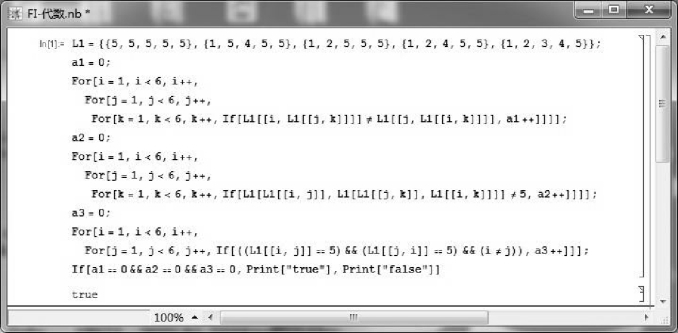
图2.1 验证(X,→, 0)是FI代数的Mathematica程序
例2.2.6 设X=[0,1],对任意的x, y∈X,定义x →y=min(x, y),即取蕴涵算子→为Mamdani蕴涵算子,则(X,→, 0)不是FI代数.
事实上,当x≠1时,x →x=min(x, x )=x≠1,这表明→不满足(FI3),从而表明(X,→, 0)不构成FI代数.
例2.2.7 设X=[0,1],对任意的x, y∈X,定义x →y=max (1-x, y),即取蕴涵算子→为Kleene-Diends蕴涵算子,则(X,→, 0)不是FI代数.
事实上,当0<x<1时,显然0 <1-x<1,从而x →x=max (1-x, x)<1,这表明→不满足(FI3),从而表明(X,→, 0)不构成FI代数.
例2.2.8 设X=[0,1],对任意的x, y∈X,定义x →y=max (1-x,min(x ,y)),即取蕴涵算子→为Zadeh蕴涵算子,则(X,→, 0)不是FI代数.
事实上,当x=0.1,y=0.8,z=0.5时,有1-x =1 -0.1 =0.9,1-y=1 -0.8 =0.2,从而
![]()
但是
![]()
这表明x→(y →z )≠y→(x →z ),即→不满足(FI1),故(X,→, 0)不构成FI代数.
定义2.2.2 设(X,→, 0)是FI代数.在X上定义一个二元关系≤满足:
![]()
则称≤是→诱导的关系.
定理2.2.1设(X,→, 0)是FI代数,≤是→诱导的关系,则对任意的x,y,z∈X,下列结论成立:
(FI6)x≤1,即,x→1=1;
(FI7)(左中立原则:left neutrality principle)1→x=x;
(FI8)如果x≤y,则z →x ≤z →y且y →z ≤x →z;
(FI9)如果x≤y且y≤z,则x≤z.
证明 (1)因为x→1=x→(0→x)=0→(x →x)=0 →1 =1,所以(FI6)成立.
(2)一方面,由(FI1)和(FI3)得另一方面,由(FI1)和(FI3)得
![]()
![]()
又因为由(FI6)得(1→x)→x ≤1,所以由定义2.2.2得((1→x)→x)→1 =1,从而由(FI4)又得(1→x)→x =1.故综合两方面,再由(FI4)便得1→x=x.
(3)设x≤y,则由定义2.2.2得x→y=1.因为
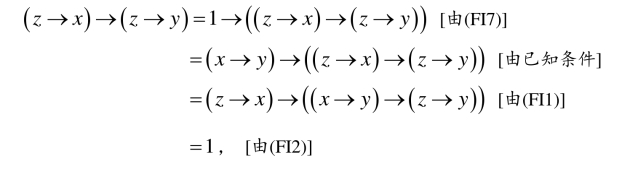
所以由定义2.2.2得z →x ≤z →y .又因为
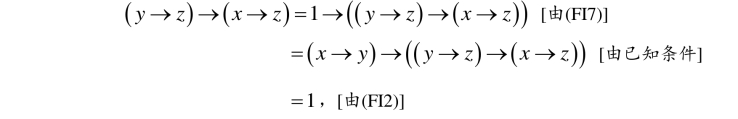
所以再由定义2.2.2又得y →z ≤x →z .因此(FI8)成立.
(4)设x≤y且y≤z,则由定义2.2.2和(FI2)可得1 =y →z ≤x →z .而由(FI6)又得x→z≤1,从而x→z=1,故由定义2.2.2便得x≤z.因此(FI9)成立.
注2.2.1 设(X,→, 0)是FI代数,≤是→诱导的关系,则由(FI3)、(FI4)和(FI9)可知(X,≤)是一个偏序集.同时,由(FI5)和(FI6)可知0和1分别为偏序集(X,≤)中的最小元和最大元.
定理2.2.2设(X,→, 0)是FI代数,≤是→诱导的关系,则对任意的x,y,z∈X,下列结论成立:
(FI10)y →z ≤(x →y)→(x →z);
(FI11) x ≤(x →y)→y;
(FI12)y ≤(x →y)→y;(https://www.xing528.com)
(FI13)((x →y)→y)→y =x →y;
(FI14)x→(y →x)=1;
(FI15)((x →y)→(x →z))→(x→(y →z))=1.
证明 (1)由(FI1)和(FI2)得
![]()
所以由定义2.2.2便得y →z ≤(x →y)→(x →z),即(FI10)成立.
(2)由(FI1)和(FI3)可得x→((x →y)→y)=(x →y)→(x →y)=1,所以由定义2.2.2便得x ≤(x →y)→y,即(FI11)成立.
(3)因为由(FI1)、(FI3)和(FI6)得
![]()
所以由定义2.2.2便得y ≤(x →y)→y ,即(FI12)成立.
(4)一方面,因为由(FI11)得x ≤(x →y)→y ,所以由(FI8)和定义2.2.2得
![]()
另一方面,因为由(FI7)、(FI2)以及定义2.2.2得
![]()
所以再由定义2.2.2得(x →y)→(((x →y)→y)→y)=1.因此,综合两方面由(FI4)便得((x →y)→y)→y =x →y,即(FI13)成立.
(5)由(FI1)、(FI3)和(FI6)得
![]()
即(FI14)成立.
(6)因为由(FI1)、(FI2)、(FI10)和(FI14)得
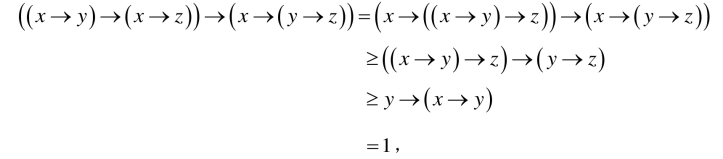
所以((x →y)→(x →z))→(x→(y →z))=1,即(FI15)成立.
定义2.2.3 设(X,→, 0)是FI代数.在X上定义一元运算C:X→X满足:
![]()
称C为X上的伪补算子,并称C (x)为元素x的伪补(pseudo-complement).
定理2.2.3 设(X,→, 0)是FI代数,C是X上的伪补算子,则对任意的x,y,z∈X,下列结论成立:
(C1)C(0 )=1且C(1)=0;
(C2)x≤CC (x);
(C3)如果x≤y,则C (y)≤C (x);
(C4)CCC (x)=C (x).
证明 (1)由(FI3)得C(0 )=0 →0 =1,由(FI1)得C(1) =1 →0 =0.
(2)因为由(FI1)和(FI3)得
![]()
所以由定义2.2.2和定义2.2.3得x≤((x→0)→0)=CC (x),因此(C2)成立.
(3)设x≤y,则x→y=1,从而由(FI7)和(FI2)得
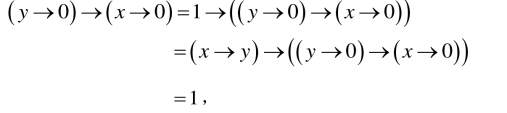
故由定义2.2.2和定义2.2.3便得C (y )=y→0≤x→0=C (x),因此(C3)成立.
(4)一方面,由(C2)显然可得C (x )≤CC (C (x))=CCC (x).另一方面,因为由(C2)得x≤CC (x),所以由(C3)得CCC (x )=C (CC (x))≤C (x).综合两方面以及≤的反对称性便得CCC (x)=C (x),因此(C4)成立.
定义2.2.4 设(X,→, 0)是FI代数,C是X上的伪补算子,如果x∈X满足:
![]()
则称x为X的正则元(regular element).由X的全体正则元构成的集合记为Re(X).
注2.2.2 设(X,→, 0)是FI代数,C是X上的伪补算子,则由定理2.2.3显然有:
(1)0∈Re(X)且1∈Re(X);
(2)对任意的x∈X,C (x)∈Re(X).
定义2.2.5 设(X,→, 0)是FI代数,∅≠A ⊆X.如果对任意的x,y∈A都有x→y∈A,则称A是X的FI子代数.由X的全体FI子代数构成的集合记为SA(X).
定理2.2.4 设(X,→, 0)是FI代数,则Re(X)∈SA(X).
证明 设x,y∈Re(X),则CC (x)=x且CC (y)=y,从而,一方面有
![]()
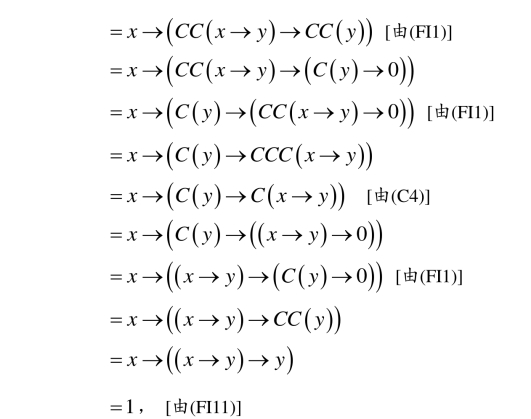
所以由定义2.2.2得CC (x →y )≤x →y .另一方面,由(C2)又得x →y ≤CC (x →y).所以综合两方面以及≤的反对称性便得
![]()
故x →y∈Re(X).因此Re(X)∈SA(X).
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




