【摘要】：定义1.4.10 设X是一个拓扑空间.如果X中任意两个不相同的点中必有一个点有一个开邻域不包含另一个点，即，如果x， y∈X，x≠y，则或者x有一个开邻域U使得yU，或者y有一个开邻域V使得xV，则称X是一个T0空间.定义1.4.11 设X是一个拓扑空间.如果X中任意两个不相同的点中每一个点都有一个开邻域不包含另一个点，即，如果x，y∈X，x≠y，则x有一个开邻域U使得yU，且y有一个开邻域V使得
定义1.4.10 设X是一个拓扑空间.如果X中任意两个不相同的点中必有一个点有一个开邻域不包含另一个点，即，如果x， y∈X，x≠y，则或者x有一个开邻域U使得y∉U，或者y有一个开邻域V使得x∉V，则称X是一个T0空间.
定义1.4.11 设X是一个拓扑空间.如果X中任意两个不相同的点中每一个点都有一个开邻域不包含另一个点，即，如果x，y∈X，x≠y，则x有一个开邻域U使得y∉U，且y有一个开邻域V使得x∉V，则称X是一个T1空间.
定理1.4.4 设（X ，T）是一个拓扑空间，则下列条件等价：
（1）X是一个T1空间；
（2）X中每一个单点集都是闭集；
（3）X中每一个有限子集都是闭集.
(www.xing528.com)
定义1.4.15 正则的T1空间称为T3空间.正规的T1空间称为T4空间.
定义1.4.16 设X是一个拓扑空间.如果对于任意的x∈X和X中任何一个不包含点x的闭集B，存在一个连续映射f ：X→［0，1］使得f（x）=0以及对任何的y∈B有f （y）=1，则称拓扑空间X是一个完全正规空间（completely normal space）.
定义1.4.17 完全正则的T1空间称为Tychonoff空间或T3.5空间.
下面，我们将满足各种分离性的拓扑空间之间的关系图示如下：
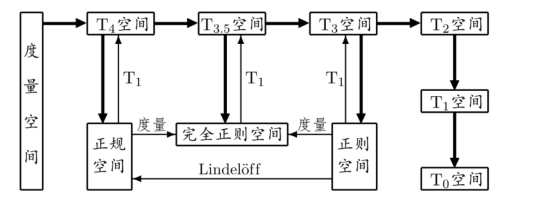
图1.3 满足各种分离性公理的拓扑空间的关系图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
