设P是论域，当需要考虑论域中对象之间相互比较的问题时，数学中常用的方法是在论域P上赋予一种称之为序结构的二元关系，并把赋予序结构的P称为序集.对于这种描述性的序和序集概念来说，其意义过于宽泛.下面我们将为读者介绍其准确的含义和基本性质.
例1.3.2 如图1.1所示，设P是黑点构成之集，规定位置较低的点不大于位置较高的点，也不大于自身，则各图中的P都是偏序集.
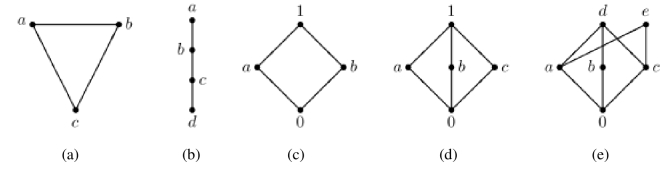
图1.1 几类偏序集的Hasse图
（1）如果对任意x∈X，有a≤x，则称a为X的一个下界；
（2）如果对任意x∈X，有x≤a，则称a为X的一个上界；
（3）设a为X的一个下界，如果对X的任一下界b均有b≤a，则称a为X的最大下界，也称下确界，记为a=infX或a=∧X；
（4）设a为X的一个上界，如果对X的任一上界b均有a≤b，则称a为X的最小上界，也称上确界，记为a=supX或a=∨X.
例1.3.4 如图1.1所示.
（1）在图（a）中，｛a ，b｝有下确界c，但没有上界；
（2）在图（b）中，｛a， b， c｝的上、下确界分别是a和c；
（3）在图（e）中，｛a， b， c｝有下确界0，X有两个上界d与e，但没有上确界.
例1.3.5在偏序集（P（X），⊆）中，设｛Aλ|λ∈Λ｝⊆P（X），则｛Aλ|λ∈Λ｝的下确界和上确界都存在，就是｛Aλ|λ∈Λ｝中各集合的交与并，即
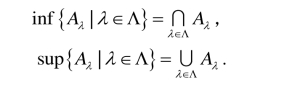(www.xing528.com)
例1.3.6 设P=［0，1］，≤是通常序且X⊆P.若X=∅，则supX=0且infX=1.这是因为：空集∅以P中的每个元素为上（下）界，上确界作为最小上界当然为0，而下确界作为最大下界当然为1.这里需要注意：当x∈∅时，x≤a（或a≤x）对P中的每个元素a都成立.
定义1.3.5 设（P，≤）是偏序集，X⊆P且a∈X.
（1）如果对任意x∈X，恒有a≤x，则称a是X的极小元；
（2）如果对任意x∈X，恒有x≤a，则称a是X的极大元.
例1.3.7 在例1.3.3中，偏序集（P（X），⊆）是定向集.
定义1.3.7 设（P，≤）和（Q，≤）是两个偏序集，φ：P →Q是映射.
（1）如果对任意的x， y∈P，当x≤y时，总有φ（x）≤φ（y ），则称映射φ是保序的（order-preserving）或单调的（monotone），有时也称之为序同态.
（2）如果对任意的x，y∈P，x≤y在P中成立当且仅当φ（x）≤φ（y ）在Q中成立，则称映射φ是保序嵌入（order-embedding）.
（3）如果φ是满的保序嵌入，则称φ是保序同构（order-isomorphism）.
一般地，如果偏序集（P，≤）和（Q，≤）之间存在保序同构，则称P和Q是保序同构的（Order preserving isomorphism），记为P≅Q.
定理1.3.2 设（P，≤）和（Q，≤）是两个偏序集，则下列陈述等价：
（1）P和Q是保序同构的；
（3）存在一一映射φ：P →Q 使得φ和φ-1：Q →P 都是保序映射.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
