直线的影子性质及应用

1.直线落在一个平面上影子的特性

（1）直线与承影面相交时，直线的影子将通过该线与承影面的交点。图12-12中直线AB与承影平面P相交于点B，则B0与B重合，而B0又在直线的影子A0B0上，故A0B0通过交点B。

图12-11　直线影子的投影作法

（2）直线与承影平面平行时，直线的影子必与直线本身平行且等长。如图12-13所示，直线AB与承影平面P平行，则通过AB的光平面与P面的交线A0B0必与直线本身平行。又因光线AA0∥BB0，故ABB0A0为一个平行四边形，AB=A0B0。

图12-12　直线与承影面相交时的影子

图12-13　直线与承影面平行时的影子

2.一直线落在两个平面上影子的特性

（1）一直线落在两个平行的承影平面上的两段影子必互相平行。如图12-14所示，因通过直线A的光平面与两个平行的承影平面P、Q的交线互相平行，故影子A01和A02必互相平行。

图12-14　一直线在两个平行平面上的影子

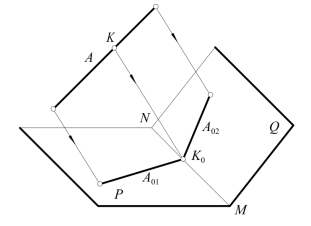
图12-15　一直线在两个相交平面上的影子

（2）一直线落在两个相交的承影面上的两段影子，必交于这两个承影面的交线上。如图12-15所示，由于三个相交平面的三条交线必相交于一点，故通过直线AB的光平面与两个承影平面P、Q所交成的两段影子A01和A02的交点K0，必位于P、Q的交线MN上，交点K0称为折影点。

3.两直线落在一个平面上影子的特性

（1）两平行直线落在一个承影平面上的两段影子必互相平行。如图12-16所示，因为通过两条平行直线AB、CD的两个光平面互相平行，与承影平面P交得的两条影子A0B0、C0D0也互相平行，且A0B0∶C0D0=AB∶CD。

（2）两相交直线在一个承影面上的两段影子必定相交，且影子的交点，为两直线交点的影子。如图12-17所示，直线AB与CD的交点E在P面上的影子E0，必同时在两直线的影子A0B0、C0D0上，因而为它们的交点。

（3）两交叉直线在一个承影面上的影子如果相交，则交点为一条直线上一点落在另一条直线上影子的影子。如图12-18所示，交叉直线AB、CD在P面上的影子A0B0和C0D0之所以会交于一点¯E0，是因为AB上一点E和CD上一点E0位于同一条光线上。E点的实际影子为E0，而为假影。(www.xing528.com)

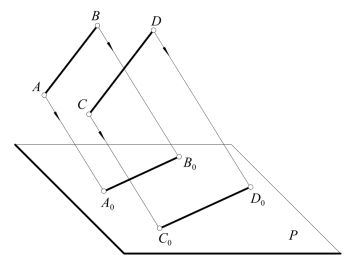
图12-16　两平行直线在一个平面上的影子

图12-17　两相交直线在一个平面上的影子

图12-18　两交叉直线在一个平面上的影子

图12-19　一直线在互相平行的两个铅垂面上的影子

[例12-1] 如图12-19所示，求直线AB落在互相平行的H面垂直面P和Q上影子的投影。

[解] 因P和Q面的H面投影有积聚性，故直线AB影子的H面投影必在积聚投影p和q上。

先作出端点A和B的影子，它们分别位于P和Q面上，故AB的影子各有一段落于P和Q面上。图中还作出了点B落于P上的假影

作连线，可得AB落在P面上影子的投影，其中段是可见的段被Q面遮住而不可见。在投影图中，凡不可见的影子一般不予表示。

再由作的平行线，与Q面左边交于，而d0必在积聚投影q的左端，由之可反求出d和d′。

4.投影面垂直线影子的投影特性

图12-20　投影面垂直线的影子

（1）某投影面垂直线落于任何物体表面上的影子，在直线所垂直的投影面上的投影必为一直线，且与通过该垂直线的光平面在该投影面上的积聚投影方向一致。如图12-20（a），H面垂直线AB落在H面和房屋各面上的影子（房屋本身的影子未画出）为折线A0C0、C0D0和D0B0，相当于通过AB的光平面与H面、房屋各面的交线。因AB垂直H面，故光平面也垂直H面，其H面投影积聚成一直线，它包含了AB各段影子的H面投影。如图12-20（b）中，过直线AB的光平面在H面上的积聚投影呈45°向，它包含了影子A0C0、C0D0和D0B0的H面投影a0c0、c0d0、d0b0。

（2）某投影面垂直线落在另一投影面平行面上的影子，在该承影平面所平行的投影面上的投影，除了与直线本身的同面投影平行外，且距离等于直线到该投影面平行面间的距离。如图12-20（a），H面垂直线AB上一段CD落在V面平行面Q（q，q′）上的影子C0D0。由于CD与Q面都垂直于H面，所以CD必平行Q面，故C0D0平行CD。从投影图中可看出，V面投影中相平行的c′d′与间距离l，等于H面投影中cd点到q的距离l（即CD与Q面间距离）。

图中还画出了端点B落于屋面上影子的作法，且可由d0b0呈45°方向，证明成对称方向。