绘制立体透视作法与画法几何

1.立体的透视

立体的透视，即为立体表面的透视。立体的表面由平面、曲面所组成，故绘制立体的透视就是绘制平面或曲面的透视。

平面立体的表面形状、大小和位置，由它的棱线所确定。故作平面立体的透视，实为作各种位置直线的透视。当作曲面立体的透视时，除了画出其轮廓线的透视外，还要画出曲面的透视外形线等。

2.视角

观看物体时，视线应在一定范围内才感舒适，并且可以使得画出的透视图不致变形过大而失真。视线间的最大夹角称为视角，视角一般应在20°～60°的范围内，而以30°左右为佳。

视角通常可由H面投影中最外视线间的夹角来控制。如图11-17，房屋的H面投影位于两条视线si2i1、sl2l1所构成夹角φ的范围内。当两旁视线不对称时，应以与主视线夹角为最大一侧的视线来量度。如图11-16中，右侧的半视角为φ/2，故视角为φ。高耸建筑物等还应注意竖直方向的视角。

3.透视种类

画面、视点可对物体有各种不同的相对位置，因而形成的透视也有不同的名称。图11-16中画面与长方体房屋的正面平行，该透视称为正面透视，图11-17中画面与房屋的两个方向墙面各成一夹角时，该透视称为成角透视，另外图11-16中，视点高于房屋，好像在高处观看，故这种透视也称为鸟瞰图。

4.立体的透视作法举例

[例11-2] 作长方体房屋轮廓的透视。如图11-16所示，已知房屋的H面、W面投影及视点S（s，s′）。设地面恰为H面，故o′x′与房屋W面投影中的底边平齐，又设画面平行于房屋的正面，且恰与侧屋的前墙重合，故ox与房屋H面投影的最前边重合。

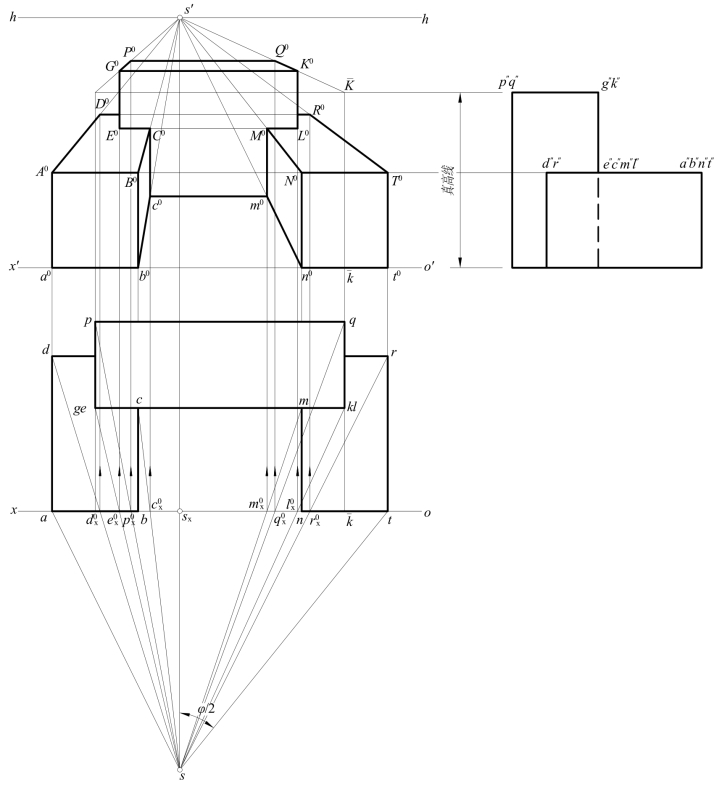
图11-16　长方体房屋轮廓的正面透视

[解] 在分别为H、V、W投影面垂直线的三组轮廓线中，其中一组侧垂线如GK等和一组铅垂线如Cc等平行画面，故它们的透视G0K0、C0c0等与相应的投影方向一致，另一组正垂线如BC等垂直画面，它们的灭点即为主点s′。

因左侧屋前墙面AabB恰在画面上，故它们的透视与本身重合，于是可先画出其透视A0a0b0B0，然后作连线A0s′，b0s′，B0s′，与过的连系线相交，得D0，c0，C0，也即得出棱线的透视A0D0，b0c0，B0C0及c0C0。用同样的方法可求得右侧屋前墙面NntT的透视N0n0t0T0及R0，m0，M0，并得出相应棱线的透视T0R0，n0m0，N0M0及m0M0，连c0m0；利用真高线¯k¯K求得QK的迹点，过的连系线与¯Ks′交得Q0，过M0的水平线与过的连系线交于L0，再由L0向上延伸连系线，与¯Ks′交得K0，同法可求得P0，E0，G0，最后连结M0L0K0Q0 P0G0E0C0，G0K0及D0R0的可见段。

[例11-3] 作坡顶房屋的透视。如图11-17所示，已知房屋的平面图、正立面图和左立面图，但它们并非按常规位置布置，其中平面图即H面投影放置成对ox呈倾斜的位置，即房屋的墙面对画面成一夹角。左立面图即W面投影排在透视图旁边，以便引出真高线高度。视点的H面投影s，以及o′x′和h—h均为已知，图中把画面即透视图布置在H面投影中的s和ox之间的空白处，以节省纸幅。

图11-17　坡顶房屋轮廓的成角透视

[解] （1）作灭点：图中除了竖直的各条墙角线因平行画面而透视方向不变外，其余的两组水平线方向如ab、bc等均与画面相交而分别有灭点F1和F2。

（2）作墙身线的透视：过b的竖直向墙角线在画面上，为真高线，b0与b重合。b0F1和b0F2与sa和sc同ox交点处的连系线交得a0，c0，故得透视a0b0，b0c0。F1c0的延长线与sd同ox交点处的连系线交得d0，得c0d0，同法可求出d0e0。通过a0、b0、c0、d0、e0等处的竖直线，即为各墙角线的透视方向。在过b0的竖直线上取真高h5得B0，F1B0与过a0的竖直线交得A0。

（3）作屋檐的透视：在平面图中，屋檐G2J2，G1J1的投影交ox于迹点，过作连系线，由h1和h4可作得真高线的延长线与过sg2g1，sj2j1同ox交点处的连系线交得透视的延长线与过sk2k1同ox交点处的连系线交得透视

至于透视，可设想利用水平辅助线K1L1和K2L2来作出。即由与过sl2l1同ox交点处的连系线交得透视，而连线可得出右方屋檐下边可见的一小段透视。同样，利用水平辅助线G1I1，G2I2，可作得左后方屋檐上的，由可得出左后屋檐下边可见的一小段透视。

（4）作屋脊的透视：延长rt2交ox于迹点，过作连系线，由h2和h4可作得真高线与过st2t1，sr同ox交点处的连系线交得透视，R0，连，再连得斜檐的透视，并连得天沟的透视。同法可利用迹点¯q可求出正屋屋面的屋脊及左方斜檐的透视。最后在B0F2上得C0，F1C0上得D0，D0F2上得E0；在上得M0，上得N0。连A0M0及E0N0的可见部分。(www.xing528.com)

[例11-4] 作进门的透视。如图11-18所示，已知进门、踏步、雨篷及窗的平面图、1—1剖面图、ox，o′x′，h-h，s。

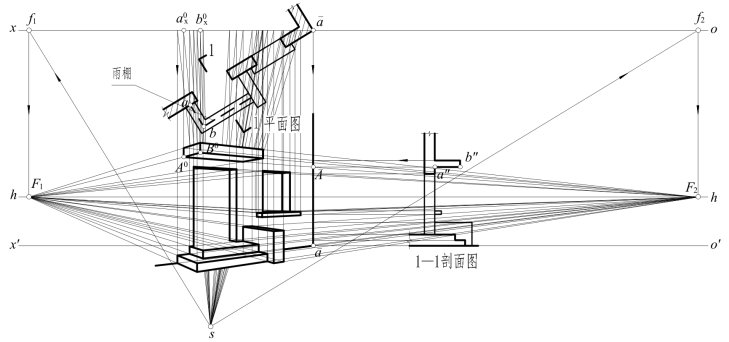
图11-18　进门的成角透视

[解] 从平面图可知：整个可见的外墙面位于ox的前方，故外墙面位于画面之前。因右外墙角线在画面上且为基面垂直线，故取该墙角线作为真高线，所有高度从1—1剖面图作水平线来获得，如点，由真高线上各点与灭点F2相连如¯AF2，再由通过外墙面上各点视线的H面投影同ox交点如处作连系线，即可作出外墙面上窗口、门洞以及雨篷、台阶与画面交成的透视如A0。再把它们与F1相连如F1A0，就可求得凸出或凹进墙面上各点的透视，如F1A0的延长线与处的连系线交得B0，即得A0B0，于是可作出全图（作图过程略）。

[例11-5] 作图11-19所示一间办公室的室内透视。已知平面图、室高、桌高及桌面厚度、窗台高及窗高、门高。

[解] 由平面图可知，画面与地面、天棚、左、右墙面交于矩形1357，透视10305070与之重合，反映了房间的宽度和高度。

正面墙壁2468平行画面。左、右墙壁的墙脚线78和12和墙顶线56和34均垂直于画面，灭点为主点s′，迹点为7，1，5，3四点。连线s′70，s′10，s′50和s′30为这些线的全透视。s42，s68与ox交点处的连系线与这些全透视交得墙角线4020，6080，并连得墙脚线2080及墙顶线4060。20406080为与10305070相似的矩形。

1030为右墙的迹线，以之为真高线，在上量取窗口高度，如点为窗顶延长后与画面交成的迹点与过处的连系线交得A0，用类似的方法可作出窗台、窗扇等透视。

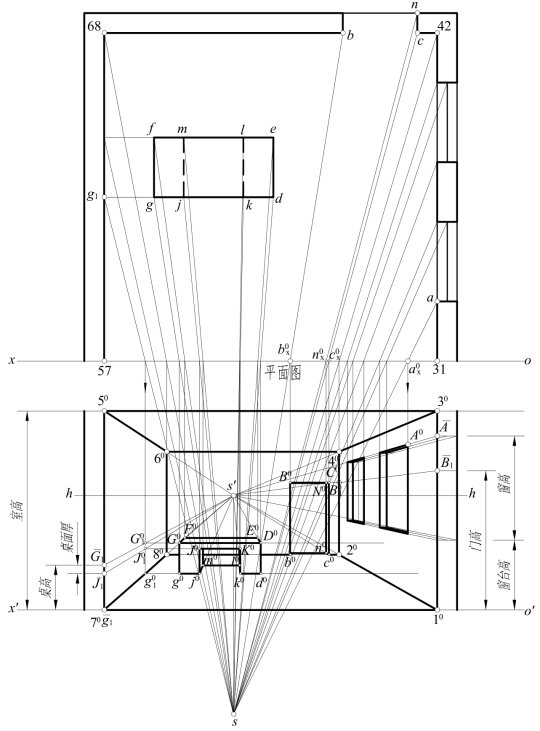
图11-19　办公室的室内透视

正面墙上门顶的透视B0C0可按门高在1030上定出，连线与2040交得，由作水平线，与过的连系线交得B0，C0。另外过的连系线与2080交得b0和c0，C0s′和c0s′与过的连系线交得N0和n0，过N0和n0作水平线至B0b0为门外侧的门顶和地面线的透视。

用作B0和C0的相同方法可求得D0，G0及K0，J0，再求得d0，g0及k0，j0。在D0s′，G0s′，k0s′，j0s′上分别求得E0，F0，l0，m0，连接相应点的透视即可作出桌子的透视。

[例11-6] 作圆柱的透视。如图11-20所示，已知置于H面上竖直正圆柱的H面投影、ox，o′x′，h—h，s及柱高h。

[解] 要作底圆和顶圆的透视，可作出其上一些点的透视顺次相连而成。利用八点法作图，先任作一个圆周的外切正方形abcd，其边线与圆周切于1，3，5，7，对角线交圆周于2，4，6，8。再作底圆和顶圆外切正方形的透视，并作出对角线的透视，在它们的透视上作出底圆和顶圆上八点的透视，并顺次相连，就可得到底圆和顶圆的透视。

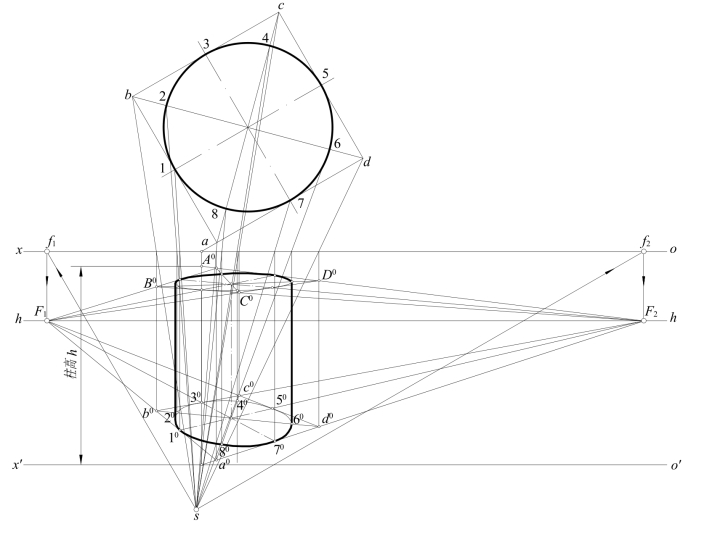
图11-20　圆柱的透视

再作底圆、顶圆透视的两条竖直公切线，即为圆柱面的透视外形线。在透视图中，顶圆和底圆的不可见部分不必画出。

[例11-7] 作拱桥的透视。如图11-21所示，已知拱桥的两面投影，并知站点s、视平线h—h及ox、o′x′轴。

[解] 根据V面投影（正立面图）中各点的高度尺寸h1，…，h5，在过D点的画面真高线上截得一系列点，并把它们与F1相连，在这些连线上可作得各点的透视G0，K0；A0，B0，C0，D0；10，30，40，60；20，50；E0，a0，b0，c0，d0，J0；在A0F2和a0F2上作得M0和m0，在C0F2和c0F2上作得N0和n0，在K0F2和J0F2上作得L0和R0；顺次连接相应点及光滑连接A0102030B0及C0405060D0（后面上两组类似的曲线作法略，只需画出可见部分）。

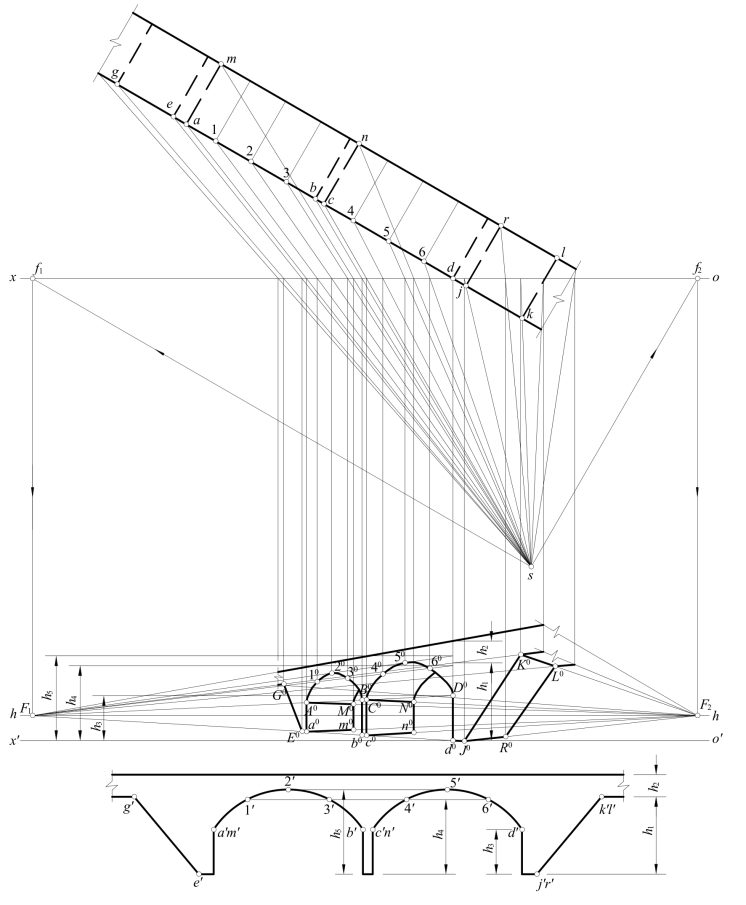
图11-21　拱桥的透视