直线透视作法，《画法几何（第6版）》

1.H面平行线的透视作法

如图11-12（a）所示，已知画面V、基面H、视点S（s）及视平线h—h。设有一条与V面相交的H面平行线AB，其H面投影为ab。AB离开H面的高度相当于投射线Aa和Bb的高度h。视线SA和SB与V面交得透视A0和B0，连线A0B0即为AB的透视。又视线Sa和Sb与V面交得次透视a0和b0，连线a0b0为ab的透视，即为AB的次透视。连系线A0a0和B0b0分别为平行于V面的竖直方向投射线Aa和Bb的透视，故仍为竖直方向。

图11-12　H面平行线的透视作法

现介绍利用直线的迹点、灭点和视线的H面投影来作透视的方法：

（1）投影图布置——如图11-12（b）所示，为了使得H面、V面上的图形不重叠，可将H、V面拆开来排列。基线OX置于水平位置，且分别以ox、o′x′表示。H面上并画出已知的ab和s。V面上画出了h—h。因为h—h为通过S的H面平行面与V面的交线，故h—h与o′x′间距离表示了视高Ss，因而不需作出s′。实际作图时，也可不必画出H、V的边框，如图11-12（c）所示。甚至，H、V的位置上下相调或交叉，将如图11-17至图11-19所示。

（2）迹点作法和真高线——如图11-12（a）所示，延长AB，可与V面交得迹点N。此时，H面上ab也必延长，与V面交于OX上的点n，则n为ab的迹点，也为N的H面投影。故投射线nN垂直OX，且长度nN反映了AB离开H面的距离，故连线nN称为H面平行线的真高线。

于是在图11-12（c）中，如已知ab，则延长后必与ox交于点n。由n作竖直线，又与o′x′交于n，由之量取高度h，即得AB的迹点N，nN即为真高线。

（3）灭点作法——H面平行线的灭点位于视平线h—h上。如图11-12（a）所示，现过S作视线SF∥AB，可与V面交得灭点F。因AB为H面平行线，故SF也为一条H面平行线，且位于通过S的水平视平面内，因而SF与V面交得的灭点F，应位于该视平面与V面交得的视平线h—h上。又因AB∥ab，故SF也必平行ab，即F也为ab的灭点。

SF的H面投影为sf，因SF为H面平行线，故sf∥SF，又因SF∥AB，ab∥AB，故sf∥ab。sf与OX的交点f，为F的H面投影，故连系线fF⊥OX。

于是在图11-12（c）中，先过s作sf∥ab，与ox交于点f，再由f作连系线fF，即可与h—h交得灭点F。

（4）由视线的H面投影作直线的透视——视线法。如上所述，如先求出AB（ab）的迹点N和灭点F，则连线NF为直线AB延长后的透视，A0B0必在其上。这种迹点和灭点的连线NF（以及延长线），也称为直线AB的全透视或透视方向。同样a0b0必在连线nF上。

现再利用视线的H面投影来定出端点A、B的透视A0、B0和次透视a0、b0的位置。如图11-12（a）所示，视线SA的H面投影为sa，也为视线Sa的H面投影。sa与OX的交点，故连系线

于是在图11-12（c）中，引连线sa，与ox交于点，过作线⊥ox，即可与NF交得透视A0，与nF交得次透视a0。

同法可求出点B的透视B0和次透视b0。于是线段A0B0为AB的透视，a0b0为ab的透视，即AB的次透视。

这种利用直线的迹点、灭点和视线的H面投影作透视的方法，称为视线法，为作建筑物的透视时最常用的基本作法，故也称为建筑师法。

2.画面垂直线的透视作法

画面垂直线的灭点为主点s′。画面垂直线必平行H面，是H面平行线的特殊情况。在图11-13中，设已知画面垂直线AB的H面投影ab，并知离开H面的高度h，作透视A0B0及次透视a0b0。

本图中，因a、b位于ox两侧，故AB穿过V面。ab与ox交得n。则由n作连系线，并在它与o′x′的交点n处作真高线nN=h，即可求得AB的迹点N。

图11-13　画面垂直线的透视作法(www.xing528.com)

平行AB的视线，为主视线Ss′，故主点s′为画面垂直线AB及ab的灭点。

由视线的H面投影sa、sb与ox的交点作连系线，即可与Ns′、ns′交得透视A0B0和次透视a0b0。

3.H面垂直线的透视作法

如图11-14（a）所示，设空间有一条高度为h的H面垂直线Aa（本图为点A的投射线），其下端a为点A的H面投影。在图11-14（b）中，已知ox、s、a及o′x′、h—h，并知高度h，作透视A0a0。

图11-14　H面垂直线的透视作法

H面垂直线也平行画面V，故透视A0a0仍为一条竖直线。通过sa与ox的交点作连系线，则A0a0必在其上。

至于端点A0、a0的位置，如图11-14（a）所示，可过A、a任作两条平行的H面平行线作为辅助线，并与V面交得迹点因a在H面上，故¯a在OX上，且，其长度等于Aa的高度h。

再作辅助线的灭点F，则连线为辅助线的全透视，必通过A0、a0。

故在图11-14（c）中，过a任作辅助线的H面投影，并在作连系线，与o′x′交得。由之量取高度h，得到。再在H面上，作，过f的连系线与h—h交得辅助线的灭点F。

可与通过的连系线交得透视

本图也相当于：已知一点A的H面投影a，并知点A离开H面的高度，求作点A的透视A0和次透视a0。

4.其他位置直线的透视作法

对于其他位置直线，如一般位置直线、画面平行线等，可以作出它们端点的透视来连成直线的透视。如能利用直线透视的其他特性，还可简化作图。

[例11-1] 设已知画面平行线AB的H面投影ab及ox、o′x′、h-h、s，又知它的左下端A离开H面的高度h，以及AB的倾角α为45°。求透视A0B0和次透视a0b0，见图11-15。

[解] （1）先过A、a分别作V面垂直线为辅助线，迹点为。它们公有灭点s′。sa与ox交点处的连系线与交得A0、a0。

（2）再作A0B0，因AB∥V面，故A0B0∥AB，即A0B0与水平方向夹角也为45°，又因ab∥V面，故a0b0∥ab，因而a0b0也为水平方向。

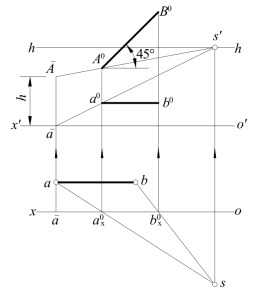
图11-15　画面平行线的透视作法

（3）于是由A0向右上方作45°直线，由a0作水平线，与过sb与ox的交点处的连系线相交，即可交得B0、b0来得出A0B0和a0b0。