曲面上各处的的坡度相同时,该曲面称为同坡曲面,各等高线的间距相同。正圆锥面即为一例。
图10-15,设通过一条曲线ABCD在前方有一个坡度2/1的同坡曲面,它可以看作是以曲线上各点为顶点的、坡度相同的各正圆锥面的包络面,因而同坡曲面的各等高线相切于各正圆锥面上标高相同的各等高线,该同坡曲面的坡度等同于各正圆锥面的坡度,也为2/1。

图10-15 同坡曲面
因此,如已知曲线的标高投影,并知同坡曲面的坡度,则以其倒数即平距为半径差来作出各圆锥面上同心圆形状的各等高线,由之可作出同坡曲面上与它们相切的一组等高线。
[例10-4] 如图10-16所示,已知地形图(具有等高线)中路面边线的水平投影以及路面上等高线的标高投影。填挖方坡度都是2/3,求道路边坡上的各等高线以及边坡与地面的交线。
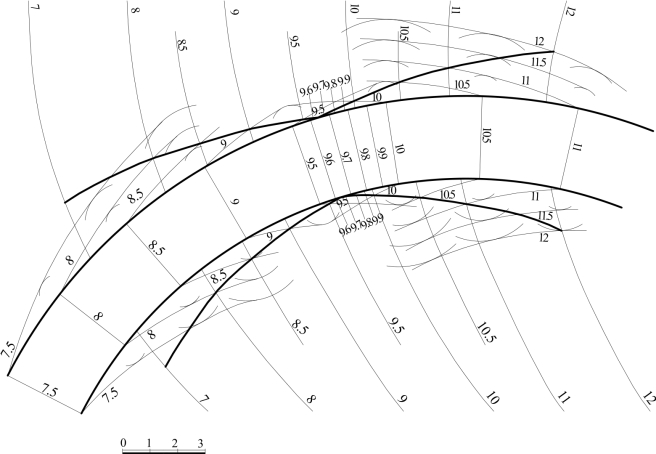
图10-16 道路的标高投影(https://www.xing528.com)
[解] 土建工程中施工时,填土石的地方,称为填方,挖土石的地方,称为挖方。其体积用m3为单位,1m3称为一方。本图中,由于左端路面的标高如8m处大于地面的标高7,故左端道路的边坡为填方,相反地,右端路面的标高如11m处小于地面的标高12,故右端道路的边坡为挖方。道路边坡为同坡曲面,这些面上等高线的间距,由坡度可算得间距为3/2,以之为半径差,按图10-15的方法,在路边上刻度8,9…处作同心圆,即可作出边坡上与它们相切的各等高线。作图时添加了标高8.5,9.5,10.5的等高线,由之可作出较多的同心圆来使得边坡上各等高线作得精确些。
边坡的各高等线同地面上标高相同的等高线交点的连线,即为边坡与地面的交线。
由地面、路面的等高线可知,道路两侧的填挖方分界点都在9.5与10之间,为做到尽量精确,在9.5与10之间又插入了9.6~9.9的地面、路面等高线,在该范围内可知分界点在9.6与9.7之间。
[例10-5] 如图10-17所示,已知地面的等高线及一水坝的圆弧形坝顶的标高投影,坝坡的i=3/2,并知坝的断面A—A和水面的标高为38.5m。试完成标高投影。
[解] 先作出坝坡的等高线,为半径差等于平距l=2/3的同心圆弧,再求出它们与地面等高线的交点,即可连得坝坡与地面的交线。图中水面与地面的交线为一条标高为38.5m的等高线。

图10-17 水坝的标高投影
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




