轴测坐标系的伸缩系数和轴间角-画法几何

表9-1所列的几种轴测投影的伸缩系数和轴间角的数值证明如下，以供参考。

1.正轴测投影

如图9-6所示，空间直角坐标系的三条坐标轴X，Y，Z与轴测投影面P交于迹线集合点PX，PY和PZ；P与三个坐标面交于迹线PXPY，PYPZ和PXPZ。

原点O在P面上的正投影OP为轴测坐标系的原点；连线OPPX，OPPY和OPPZ位于轴测轴XP，YP和ZP上，为空间坐标轴上长度OPX，OPY和OPZ的轴测投影，故各轴的伸缩系数为：

轴间角为∠PXOPPY，∠PYOPPZ和∠PXOPPZ。

（1）正轴测投影的性质一：三个轴向伸缩系数的平方和等于2。

在图9-6中，投射线OOP与X，Y，Z轴夹角分别为α1，β1和γ1；三条轴测轴与X，Y，Z轴的夹角分别为α，β和r。则α=90°-α1，β=90°-β1和γ=90°-γ1。在直角三角形OOPPX，OOPPY和OOPPZ中：

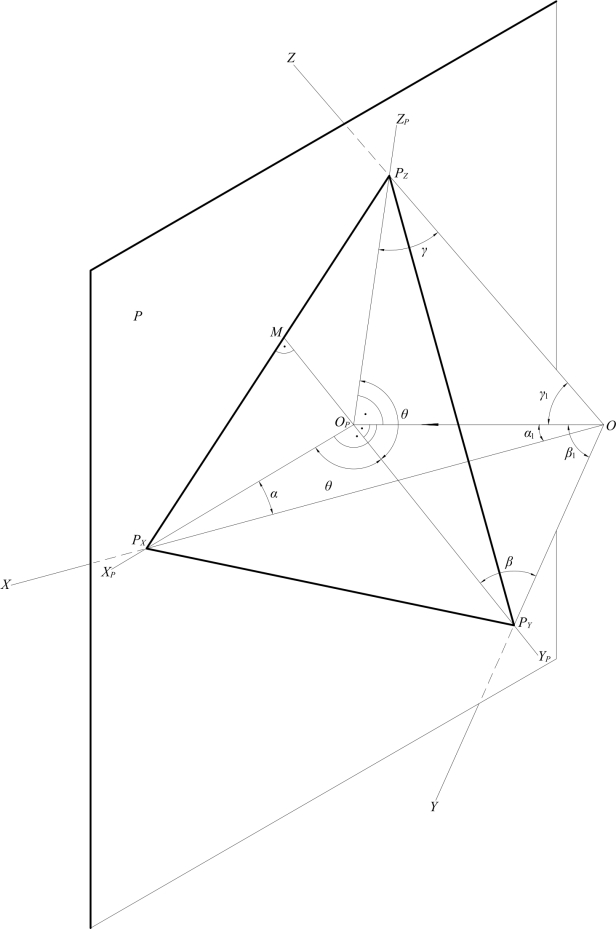
图9-6　空间直角坐标系的正轴测投影

由空间解析几何中余弦定理可知：

①正等轴测投影的伸缩系数p=q=r，由式（1）得

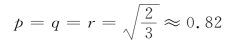(www.xing528.com)

②正二等轴测投影的伸缩系数，因p=r，q=即p=r=2q，故得

（2）正轴测投影的性质二：每条轴测轴是迹线三角形的高线。

如图9-6中，延长PYOP交迹线PXPZ于M点，迹线PXPZ是轴测投影面P与空间坐标面XOZ的交线。因投射线OOP垂直P面，故OOP垂直PXPZ；又因OPY垂直XOZ，故OPY垂直PXPZ。即PXPZ垂直△OOPPY，则PXPZ也垂直OPPY（即轴测轴YP）。同理可证明XP垂直PYPZ，ZP垂直PXPY，故每条轴测轴是迹线△PXPYPZ对应边上的高。

①正等轴测投影的轴间角——由于三个伸缩系数相同，故α=β=γ，迹线△PXPYPZ为等边三角形，OP为其中心，故三个轴间角PXOPPY=PYOPPZ=PXOPPZ=360°/3=120°。

②正二等轴测投影的轴间角——设p=r，则α=γ，OPPX=OPPZ；另△OPPYPX≌△OPPYPZ，则PYPX=PYPZ，故△PXOPPZ，△PXPYPZ均为等腰三角形。又设长度OPX=OPZ=1，则PXPZ=。又OPPX=OPPZ=1×p=1×r=于是MPX=MPZ=

又由性质二，OPM⊥PXPZ，故△OPPXM和△OPPZM为两个全等的直角三角形，因此：

此外，利用tan（97°10′-90°和tan（131°25′-90°），得出表9-1中所示的1∶8和7∶8作出OPXP和OPYP的方法。

2.正面斜轴测投影

图9-7　空间直角坐标系的正面斜轴测投影

如图9-7所示，空间直角坐标系OXYZ的坐标面XOZ平行轴测投影面P，因此轴测轴OPXP，OPZP同原坐标轴，方向和长度均不变。而Y轴由于不平行P面，在不同方向的投射线作用下，在P面上也形成不同方向和长度的轴测轴OPYP，而在实际应用中一般使OPYP与水平方向的夹角为30°，45°或60°，以便利用三角板作图，伸缩系数一般取

相应地，对于水平斜轴测投影，使坐标面OXY平行水平的轴测投影面，并按任意方向投射，得任意方向和长度的OPZP。一般使OPXP与水平方向成30°，45°或60°，OPZP成竖直方向。伸缩系数一般取r=1。