同心球面法：特殊情况相贯线

1.相贯线的形状——圆周、椭圆

（1）相贯线为圆周。如图8-39所示，两同轴的旋转面必相交于垂直轴线的圆周，该圆周为它们公有的纬圆。当轴线垂直于投影面如H面时，这些圆周的H面投影反映了实形，V面投影则积聚成水平方向直线。

两旋转面相切又为其特殊情况，如图8-40所示。这时的相贯线成为两曲面的相切圆周，也即公有的一个纬圆。由于在相切处锥面与球面是光滑连接，实际上不存在任何线，故在图中不必画出相切圆周。

图8-39　同轴旋转面相贯

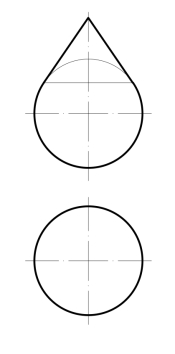
图8-40　圆锥与圆球相切

（2）相贯线为椭圆。如图8-41所示，圆锥与圆柱公有内切球，图8-42所示两圆柱也公有内切球，它们的相贯线均为两个椭圆。公有内切球的两个圆柱，实际上是直径相等和轴线相交的两圆柱。当轴线正交时，两个椭圆的大小相等；当轴线斜交时，则两个椭圆的大小不等。公有内切球的两圆锥的相贯线也为两个椭圆（未图示）。

在这几个图中，因两旋转面的相交轴线均平行V面，所以相贯线的V面投影均积聚成直线。积聚直线的交点为两椭圆前、后两个交点的重影，也为两个曲面的相切点。

图8-43为十字拱顶，它由内、外直径各为相等的两个管状半圆柱柱面所构成。内外圆柱面分别相交成两个半椭圆。它们的H面投影积聚成两段十字形直线，V面投影则在半圆柱面的积聚投影上。

图8-41　公有内切球的圆锥与圆柱相贯

图8-44（a）为由一节节薄壁圆柱面连续相交所构成的弯头在平行于柱面轴线的V面上的投影。这些圆柱面的半径R相等，且轴线相交，故相贯线为一个个椭圆，其V面投影则积聚成为一段段直线。本例是一个直角弯头，由两个全节B、C和首尾两个半节A、D组成。从图中可以看出，因各个半节所对应的圆心角相等，故各椭圆的积聚投影长度也相等，因而各个椭圆的长、短轴的长度也分别相等，即椭圆的大小相同。

如将弯头隔节调换方向，可拼成一个圆柱面，如图8-44（b）所示。图8-44（c）是其展开图。显然，由于各节的展开图可以拼成一个矩形，故能节省材料。

2.相贯线的投影作法——辅助球面法

旋转面处于特殊情况时，可用辅助球面法作相贯线的投影。根据一系列辅助球面的球心是否相同而分成两种：

（1）同心球面法

用同心球面法求作两曲面的相贯线，要满足下列三个条件：①两曲面都是旋转面；②两旋转轴相交；③两旋转轴同时平行某投影面。以两轴线的交点为球心，作辅助球面，必与两个旋转面各交于一个纬圆，两个纬圆的交点即为相贯点。于是通过作一系列的辅助球面，可得出若干相贯点，即可顺次连得相贯线。这种使用球心相同的一系列辅助球面作相贯线的方法，称为同心辅助球面法，简称同心球面法。

根据图8-39，当圆球的球心位于平行某投影面的旋转轴上时，则旋转面与圆球面交得的纬圆在这个投影面上的投影积聚成直线。辅助球面与两旋转面交得纬圆的积聚投影（直线段）间的交点，即为相贯点的投影，再求得其他投影面上的投影。

如果两相交的旋转轴不同时平行于任一投影面，则可利用投影变换的方法，使其与投影面平行。

图8-42　公有内切球的两圆柱相贯

[例8-18] 如图8-45所示，求旋转面与轴线倾斜的柱面的相贯线。(www.xing528.com)

图8-43　十字拱

图8-44　直角薄壁弯头

[解] 由于两个曲面具有同一个平行V面的对称平面，故相贯线前后对称，因而相贯线的V面投影成为重影，H面投影则前后对称。

在V面投影中，因两个曲面的投影外形线的交点为空间外形线上相贯点A1和A2的V面投影，故可直接定出，并由之求出H面投影a1，a2。

至于其他的相贯点，由于符合前述三个条件，故可用同心球面法作出。设以两曲面的轴线交点O为球心作辅助球面，即在V面投影中，以o′为圆心，R为半径作圆弧m′，为辅助球面的V面部分投影外形线。该辅助球面分别与旋转面和柱面交于纬圆L1，L2，它们的V面积聚投影的交点，即为相贯点B的V面投影b′，向下作连系线与l1交于b。同法可作出C、D等点。

图8-45　旋转体与圆柱体表面的相贯线

辅助球面的大小是有一定限制的。最大球面为通过外形线上距球心最远的相贯点A1，即最大球面半径为。最小球面则为内切于两个旋转面中的那个较大的内切球面。

从本例中可以知道，在旋转轴平行于投影面时，可以不利用其他投影面上的投影，单独地用球面法作出相贯线在这个投影面上的投影。

（2）变心球面法

用变心球面法作两曲面的相贯线，要满足下列三个条件：①一个为旋转面，另一个旋转面为一系列圆周曲线所引成；②旋转面的轴线与圆周曲线的轴线（过圆心的圆周平面的垂线）相交；③两轴线同时平行于某投影面。这时，可把旋转面轴线与另一曲面上圆周曲线轴线的交点取为球心，并通过该圆周曲线作一辅助球面，该辅助球面必与旋转面交于纬圆，纬圆与圆周曲线的交点，即为相贯点。通过一个曲面上的一系列圆周曲线，可作得一系列的圆周轴线、球心和作出一系列的辅助球面，因而交得一系列的相贯点，即可顺次连得相贯线。由于各圆周曲线的轴线位置是不同的，使得球心的位置随之变动，所以这种使用球心位置变动的一系列辅助球面求作相贯线的方法，称为变心辅助球面法，简称变心球面法。

图8-46　变心球面法作相贯线

[例8-19] 如图8-46所示，求圆台面与环面相贯线的V面投影。

[解] 由于两个曲面具有同一个平行V面的对称平面，故两曲面前后对称，相贯线也前后对称，因而相贯线的V面投影成为重影。

V面投影外形线的两个交点，也为两个相贯点的V面投影，可以直接定出。

两曲面虽均为旋转面，但轴线交叉垂直并不相交，故不能使用同心球面法解。但由于环面是以圆周曲线为母线绕O2旋转而形成，被通过O2的V面垂直面截得圆周曲线L，其V面投影l′积聚成直线，且L的轴线位于圆台面和环面共同的对称平面上，必与O1轴相交，故符合上述的三个条件，可使用变心球面法解。

以L的轴线与O1轴的交点为球心，并通过L作一个球面，与圆台面交得纬圆L1，则L与L1的交点A1，A2即为相贯点。在V面投影中，l′与交得重影点

再通过O2作V面垂直面与环面交得圆周曲线K，K的轴线与O1轴交得球心，以OK为球心，通过K作一个球面与圆台面交得纬圆K1，于是得到k′与k1′的交点b1′b2′，为相贯点B1，B2在V面上的重影。同法可求出一系列相贯点的V面投影后顺次连得相贯线。

从图中可以看出，两个球心OL和OK不是同一点。