画法几何（第6版）：正圆锥面投影及展开图

1.正圆锥面的投影

（1）正圆锥面的形成和投影图——以相交两直线之一为轴线，另一直线为母线旋转而形成的曲面，称为正圆锥面，简称圆锥面。图8-16中轴线垂直于H面。交点S称为顶点，圆周K称为底圆。所有直素线均通过顶点S。

正圆锥面的H面投影是一个圆周，为底圆的投影，圆心相当于顶点和底圆心的重影，也为轴线的积聚投影。

正圆锥面的V面和W面投影都是等腰三角形。铅直的细单点长画线是锥轴的投影，称为投影的中心线。底边为底圆K的积聚投影。V面投影三角形的两腰，即投影外形线s′a′和s′b′，是圆锥面与通过轴线的且平行于V面的对称平面与锥面相交成的、为空间外形线的最左和最右素线SA和SB的投影，与它们对应的W面投影s″a″和s″b″，则与正圆锥面轴线的W面投影重合，不予表示，即仍用中心线表示；H面投影sa和sb，成一条水平线，与H面投影圆周的中心线重合，也不予表示。三角形范围是可见的前半个和不可见的后半个锥面的重影；其对应的H面投影，分别是下半个和上半个圆形；其对应的W面投影，分别是右半个和左半个（空间应为前半个和后半个）投影三角形。

图8-15　圆柱的贯通孔和切口

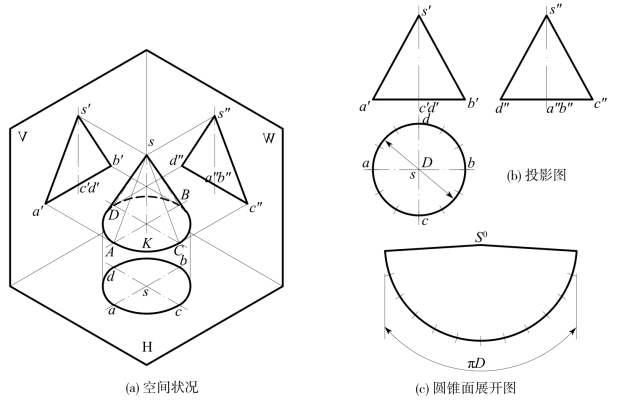
图8-16　正圆锥

同样，W面投影中三角形两腰，即投影外形线s″c″和s″d″，分别是锥面上对W面的空间外形线（最前和最后两素线）SC和SD的投影，与它们对应的H面投影sc和sd，与H面投影圆形的竖直中心线重合；与它们对应的V面投影s′c′和s′d′，则与V面投影的中心线相重合。三角形范围是可见的左半个和不可见的右半个锥面的重影；其对应的H面投影，分别是左半个和右半个圆形；其对应的V面投影也分别是左半个和右半个投影三角形。

圆锥面也可由两个投影表示，但其中之一应是显示底圆形状的投影，即本图中不宜仅用V面和W面投影来表示。

（2）圆锥体的投影——如将圆锥面的底圆作为圆锥体的底面，则图8-16（b）也是一个正圆锥体的投影图。

（3）圆锥面的展开图——正圆锥面的展开图是一个扇形，如图8-16（c）所示。因为正圆锥面的各素线等长，且素线交于一个公共的顶点，故展开图是半径等于素线长度、弧长是底圆周长度πD的一个扇形。由于正圆锥面的V面、W面投影中任一外形素线都反映了锥面素线的实长，例如s′a′。故作展开图时，任选一点S0为圆心，以s′a′为半径作圆弧。再把底圆分成若干等分，本图中为十二等分，即把底圆等分点间弦长近似地作为弧长，在展开图的圆弧上量取同样数量的弦长，近似地作为弧长。最后将起点和终点与S0相连，就得正圆锥面的展开图。

2.轴线为一般位置直线时正圆锥面的投影

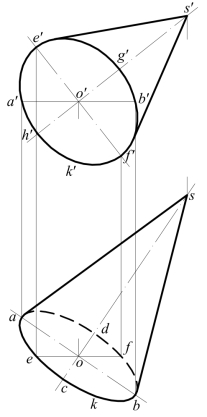
图8-17　斜置正圆锥

如图8-17所示，已知一个斜置的正圆锥。轴线为SO（so，s′o′），S为顶点，O为底圆心，底圆直径长度为D。求正圆锥的投影图。

因轴线SO为一般位置直线，故与它垂直的底圆平面为一般位置平面，因而底圆K的H面、V面投影k、k′均为椭圆，可用多种方法作椭圆，现以求出投影椭圆的长、短轴来作出投影椭圆。

因轴线垂直于底圆，也必垂直于任一条底圆直径。又因K的H面投影k的长轴是底圆上一条与H面平行的直径AB的H面投影ab，因AB⊥SO，故ab⊥so，且ab的长度等于底圆直径D。对应的V面投影为水平线a′b′。K的H面投影椭圆k的短轴cd，必位于ab的中垂线上，这里与so重影（cd长度待定）。

同理，底圆K的V面投影椭圆k′的长轴e′f′⊥s′o′，长度也等于D，对应的H面投影也为水平线ef。而短轴g′h′位于e′f′的中垂线上，与s′o′重影（g′h′长度待定）。

现在，H面投影k上除了长轴ab外，尚知一点e或f。于是可用图7-12的方法求短轴cd，同样可作出圆周K的V面投影k′的短轴g′h′。于是可用图7-9的四圆弧近似法作出k及k′。

顶点S与底圆K上任一点的连线为圆锥面的素线。在H面投影中，由s向k所引的切线为最外侧素线的投影，故为H面投影外形线，共有两条。但应注意，切点并非是端点a，b。如锥高很矮，s或s′位于底圆的投影椭圆内，则无投影外形线。

底圆的可见性可以利用底圆与轴线的同名投影的重影点来判别（本图略）。如H面投影中，因底圆不可见，故相应的d旁的k画成虚线。V面投影中，底圆为可见，故整条k′全部为实线。

3.轴线为投影面平行线时正圆锥面的投影

如图8-18所示，已知正圆锥面的轴线SO（so，s′o′，s″o″）为V面平行线，顶点为S，底圆K的圆心为O，直径长度如图中下方线段D，作圆锥的三面投影。

（1）V面投影：因SO平行V面，故与它垂直的底圆平面垂直V面，因而底圆K的V面积聚投影k′垂直s′o′，为K上一条为V面平行线的直径CD的反映实长D的投影c′d′，连线s′c′，s′d′为锥面的V面投影外形线。

（2）H面投影：因底圆所在平面倾斜于H面，故底圆K的H面投影k是一个椭圆，长轴ab垂直so，长度为D；短轴cd为K上V面平行线CD的H面投影，其端点可由V面投影c′，d′作连系线来定出，于是可作得k。由s作k的两条切线，为H面的投影外形线。因底圆为不可见，故右小半个椭圆画成虚线。

（3）W面投影：底圆K也倾斜于W面，故W面投影k″为一个椭圆，长轴a″b″垂直s″o″，长度为D；短轴c″d″为K上V面平行线CD的W面投影，与s″o″重影，可由c′、d′作连系线来交得c″、d″点，于是可作得k″。由s″作k″的两条切线，为W面投影外形线。由V面投影可知，朝向W面观看时，K全为可见，则k″全用实线表示。

图8-18　轴线平行V面时的正圆锥

[例8-7] 图8-19为由8片斜置的正圆锥面上方部分组成的屋面。整个屋面的轴线为H面垂直线SO，顶点为S。每片屋面的顶点也为S，但轴线呈倾斜位置。每片屋面屋檐的下方两端支于一个正八边形的端点Ⅰ（1，1′），Ⅱ（2，2′），…处。正八边形的中点即为点O。8片屋面高度相同。连线SⅠ，SⅡ，…为相邻两片屋面的交线，也为各锥面的直素线。故本屋面也相当于一片屋面陆续旋转360°/8=45°后的位置。

[解] 8片屋面的H面投影形状相同，仅方向不同，它们的作法相当于图8-17和图8-18的H面投影。V面投影中，s′1′2′相当于图8-18V面的部分投影，s′6′5′则与其对称；s′2′3′相当于图8-17V面的部分投影，s′5′4′则与其对称；s′3′4′相当于图8-18W面的部分投影。

整个屋面，在图的H面投影中，后方3片未画出，其V面投影与前方3片重影。

4.正圆锥的截断

正圆锥截交线的形状：平面截断正圆锥面时，由于截平面与正圆锥面相对位置不同，会得出形状不同的截交线，如表8-2所示。

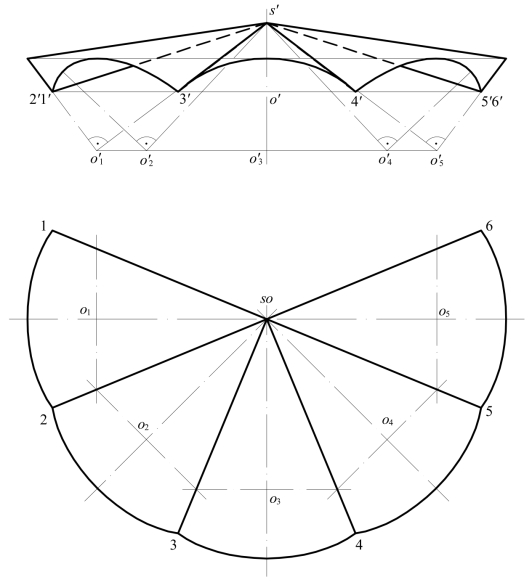
图8-19　锥面片屋面

表8-2　正圆锥截交线形状

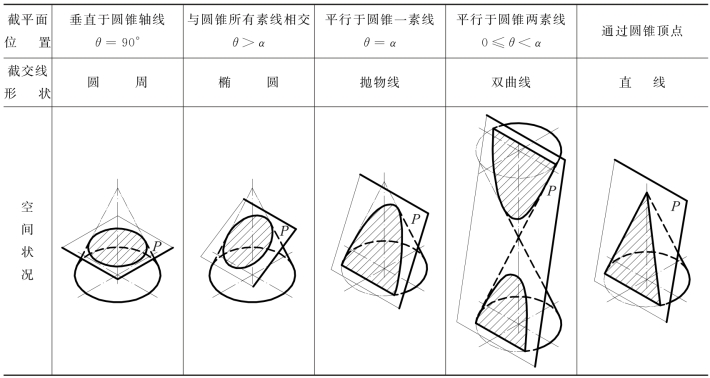
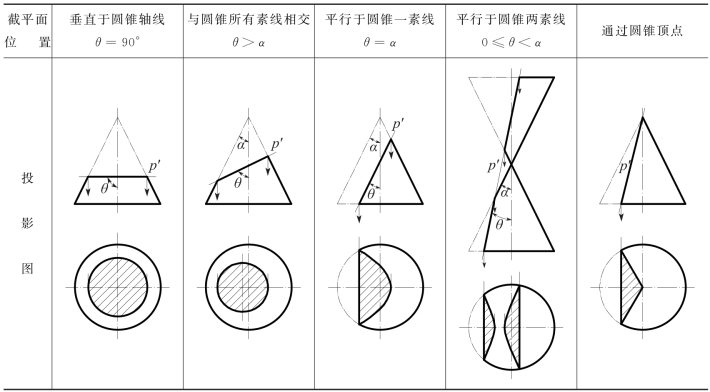
①当截平面垂直于正圆锥面的轴线时，截交线为圆周；②截平面与所有素线不平行而相交时，截交线为椭圆；③截平面平行于圆锥面的一条素线时，截交线为抛物线，轴线平行于该素线；④截平面平行于圆锥面的两条素线时，截交线为双曲线，双曲线的渐近线平行于这两条素线；⑤截平面通过圆锥面的顶点时，截交线成为两条素线。其中，椭圆长轴的一个顶点、抛物线和双曲线的顶点，均为离开锥顶最近的点。

[例8-8] 如图8-20所示，求正圆锥与V面垂直面P（p′）相交时截交线K的投影、截断面实形和截断后下半部锥面的展开图。

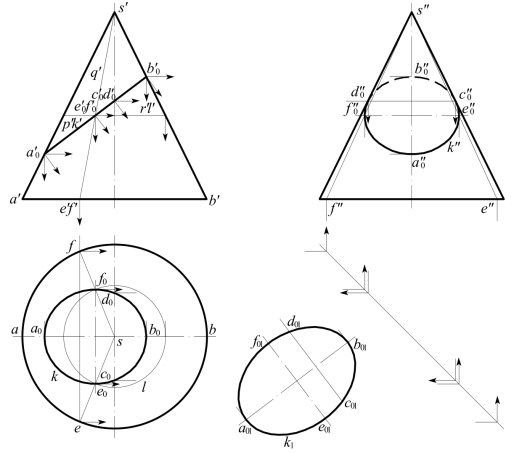
图8-20　正圆锥截交线和截断面实形的作法

[解] （1）截交线：在V面投影中，截断面的积聚投影p′与锥轴斜交，且与锥面上所有素线都相交，故P与圆锥面的截交线K是一个椭圆。

K的V面投影k′积聚在p′上而为一直线，K的H面、W面投影k和k″仍是椭圆，可求出一些截交点的投影来连得；或者由长、短轴直接作出椭圆投影。

（2）截交点作法

①积聚投影法——根据截平面P的积聚投影，通过锥面上取点来求出截交点的投影。如在p′上任取一点，作为锥面上前、后两个截交点E0和F0的V面投影。通过可在锥面上引两素线SE和SF的V面投影s′e′和s′f′，并作出它们的H面和W面投影se，sf和s″e″，s″f″，于是可作得e0，f0和。也可过引一个纬圆L的V面投影l′，由之求出l。再由引连系线，在l上定出e0，f0，由之可作出

同法可求出一些特殊点，如最高、最低点A0，B0（椭圆长轴端点）和W面投影外形线上的点C0，D0的三面投影，本例中刚好为的中点，E0和F0也是特殊点（椭圆短轴端点）。特殊点必须全数作出，再适当作出一些中间点。

②辅助平面法——●过顶点S取V面垂直面Q（q′）为辅助平面，则与锥面交于直素线SE（se，s′e′，s″e″）和SF（sf，s′f′，s″f″），并与P面交于直线），于是可交得截交点；●作水平的辅助平面R（r′）与P面交于直线E0F0，也可交得截交点E0，F0。

从上列几种作法可以看出，它们仅是理解和作图方法的不同。至于作图线，素线法与过顶点作辅助平面几乎相同，纬圆法与作水平辅助平面几乎相同。素线法和纬圆法在作图时各有优缺点。如H面投影中，锥面上靠近竖直中心线附近的点，因素线的H面投影较陡，与竖直连系线间夹角甚小而使交点e0位置不易准确，故以纬圆法为好；相反地，靠近水平中心线附近的点，则以素线法为好。

③直接作截交线的投影椭圆：A0B0为截交椭圆的长轴，短轴E0F0必过A0B0的中点，且垂直于V面，由于E0F0平行H面和W面，故A0B0和E0F0的H面和W面投影a0b0和e0f0、分别互相垂直，为投影椭圆k和k″的长、短轴。根据长、短袖可作出投影椭圆k和k″。但W面投影椭圆的长、短轴可能互换，如本题中椭圆的长轴A0B0的W面投影，反而比短轴E0F0的W面投影短。

（3）可见性：因圆锥面的H面投影全部可见，故k也全部可见而画成实线。W面投影中，因椭圆弧C0A0D0位于可见的左半个圆锥面上，故画成实线；而椭圆弧C0B0D0位于不可见的右半个圆锥面上，故画成虚线。位于投影外形线上的点为可见与不可见的分界点。

（4）截断面实形：可用辅助投影面法，以平行于P的平面作为辅助投影面H1。

作法一——求出一些截交点的辅助投影a01，e01，…来连得椭圆k1。(https://www.xing528.com)

作法二——求出长、短轴A0B0和E0F0的辅助投影a01b01，e01f01来作椭圆k1。

图中用平行于p′的椭圆k1的长轴a01b01来代替辅助投影轴

（5）展开图：如图8-21所示，先在投影图中，将底圆分成若干等分，本图为12等分，并作出过等分点的锥面素线，即可画出带有等分点处素线的整个圆锥面的扇形展开图。然后，由V面投影中量取实长来定出素线上各截交点在展开图中的位置。本图中采用旋转法，由各截交点的V面投影作水平线，与反映实长的V面投影外形线的交点来确定实长。如由作水平线，相当于点C0绕锥轴旋转时旋转圆周的V面积聚投影，与外形素线s′a′交得，该外形素线s′a′相当于通过点C0的素线SC绕锥轴旋转到与V面平行的位置，与素线SA重合。

于是在展开图上，在S0C0上取，得。同样地可作出其他各点，即可连得截交线K的展开图K0。

图8-21　正圆锥面截断后下半部分的展开图

图中用细双点画线表示截断后圆锥面上半部分的展开图。如在圆锥面截断后下半部分的展开图上，再加上底面和截断面的实形，便成为下半部分圆锥体的全部表面展开图。

圆锥面截交线为抛物线：在图8-22中，垂直于V面的截平面P（p′）平行圆锥面上一条素线SA（s′a′），故截交线K为一条抛物线，V面投影k′积聚于p′上，H面投影k也为一条抛物线，可用前述求圆锥面上椭圆截交线的各种方法，求出k上各点来连得k。

现利用抛物线的特性来作k：本图中，因圆锥面和截交抛物线均对称于过圆锥轴线且平行V面的平面，故抛物线轴线的H面投影与圆锥面的H面投影中心线ab重合。抛物线K的顶点A1位于圆锥面的外形线SB上，于是由可求出a1。P（p′）与底圆的交点和为抛物线上的点。按图7-17的作法，可先作出点b1，b2处切线，即由b1b2的中点c，在ab上由点a1量取长度a1b=a1c。又从V面投影中可知为等腰三角形，故b恰位于底圆上。于是可用图7-17的包络线法作出k（图中作图线略）。

圆锥面截交线为双曲线：在图8-23中，垂直于V面的截平面P（p′）平行圆锥面上两条素线和，故截交线K为一条双曲线的一支，其渐近线U1和U2平行于SC1和SC2。V面投影k′积聚于p′上，H面投影k也为双曲线的一支，可用前述求圆锥面上椭圆截交线的各种方法，求出k上各点来连得k。

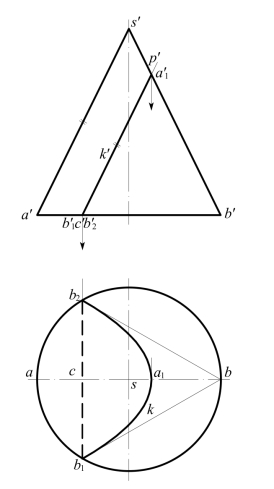
图8-22　圆锥面截交线为抛物线

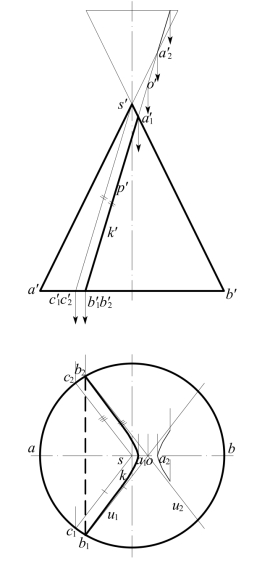
图8-23　圆锥面截交线为双曲线

现利用双曲线的特性来作k：本图中，因圆锥面和截交双曲线均对称于过圆锥轴线且平行V面的平面，故双曲线实轴的H面投影与圆锥面的H面投影中心线ab重合。P（p′）与底圆交于点。为作图需要，作出圆锥面的对顶锥面，投影p′与外形线交得双曲线顶点A1，A2和中心O的V面投影和o′，由之可作得a1，a2和o，于是过o作sc1，sc2的平行线，为k的渐近线u1，u2。实际上，由a1，a2及另一点如b1，也可作出u1，u2（图7-20），于是可用图7-22的弦线法作出k（图中作法略）。

5.正圆锥的贯穿点

求直线与曲面立体的贯穿点时，除利用积聚投影法，还可利用辅助平面法，但选用的辅助平面，应使它与曲面交得辅助截交线的投影为易于绘制的直线和圆周等。

[例8-9] 如图8-24所示，求V面垂直线L与圆锥的贯穿点。

[解] 因L的V面投影l′有积聚性，故贯穿点L1和L2的V面投影与l′重合而不需求作。求H面投影时：

（1）可过L作一辅助平面平行H面，则辅助截交线为纬圆，其H面投影为一个等大的圆周，于是可定出其与l的交点l1和l2，即为贯穿点的H面投影。

（2）也可过L及顶点S作垂直于V面的辅助平面，则辅助截交线为直素线SB1，SB2。于是sb1，sb2与l交得点l1，l2即为贯穿点的H面投影。

（3）实际上，贯穿点L1，L2的V面投影与l′重合而已知，于是成为已知圆锥面上点的一投影求另一投影问题。为此，可利用纬圆法或素线法求出l1、l2。

因圆锥面对H面都是可见的，故截交点和其旁L也为可见的，故交点外的l画成实线。

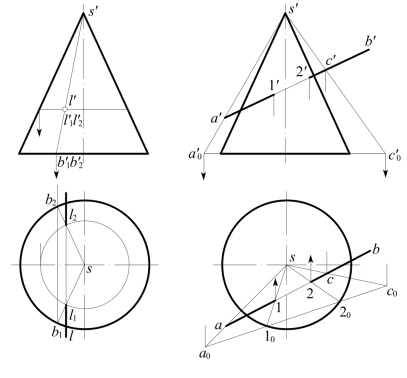
图8-24　投影面垂直线贯穿圆锥

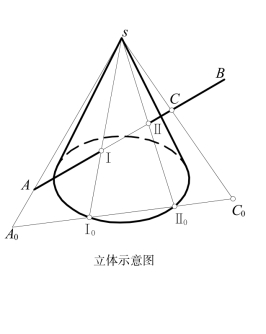
图8-25　一般位置直线贯穿圆锥

[例8-10] 如图8-25所示，求一般位置直线与圆锥的贯穿点。

[解] 如过直线AB作投影面垂直面为辅助截平面，辅助截交线将为非圆周曲线而作图麻烦。现过锥顶与直线AB作一辅助截平面，可与锥面交于直素线而作图方便。

为此，过锥顶S与直线AB上任意两点A和C作辅助线SA（sa，s′a′）和SC（sc，s′c′）。并求出与锥底平面的交点。连线A0C0（a0c0）为辅助截平面与锥底平面的交线。其与底圆交于两点Ⅰ0（10）和Ⅱ0（20）。由之可作出辅助截交线SⅠ0（s10）和SⅡ0（s20），就与ab交得截交点Ⅰ，Ⅱ的H面投影1，2。再作连系线求出V面投影1′，2′。

可见性：在两投影中，因截交点Ⅰ和Ⅱ均位于可见的锥面上，故直线AB上位于截交点以外线段均为可见而画成实线。

6.正圆锥体的相贯线

[例8-11] 如图8-26所示，求正圆锥和三棱柱的相贯线。

[解] （1）相贯线形状：从投影图中可以看出，三棱柱完全贯穿圆锥，形成两组前后对称且封闭的相贯线。每组相贯线由三段截交线（一段圆弧和二段左右对称的椭圆弧）组成，截交线间的交点为三棱柱中三条垂直于V面的棱线与锥面的贯穿点。

（2）相贯线的投影：V面投影与三棱柱棱面的积聚投影重合，故只需求H面和W面投影。

图8-26（a）采用了水平的辅助平面P，Q，R等，它们分别与圆锥面交得平行于H面的圆周，与棱柱面交得垂直于V面的直线，两者的交点即为相贯点。由于P面重合于水平棱面，故不仅求得棱面与锥面交得的两段圆弧，同时也求出了棱线与锥面的贯穿点。顺次连接同一棱面上的所得各点，即组成相贯线。

在图8-26（b）中，采用了通过锥顶的V面垂直面P，Q等为辅助平面。它们分别与圆锥面交得两条直素线，与棱柱面交得垂直于V面的直线，二者的交点即为相贯点。

图8-26　三棱柱与圆锥相贯

（3）可见性：H面投影中，圆锥面是全部可见的，棱柱面的水平棱面也是可见的，故两段圆弧可见而画成实线。四段椭圆弧因位于不可见的斜棱面上，故画成虚线。

W面投影中，相贯线左右对称，可见和不可见的相贯线重影，故仍画成实线。

[例8-12] 如图8-27所示，求正圆锥与正圆柱的相贯线。

[解] （1）相贯线形状：从投影图中可以看出，圆柱完全穿过圆锥，形成两组左右、前后对称且封闭的相贯线（空间曲线）。

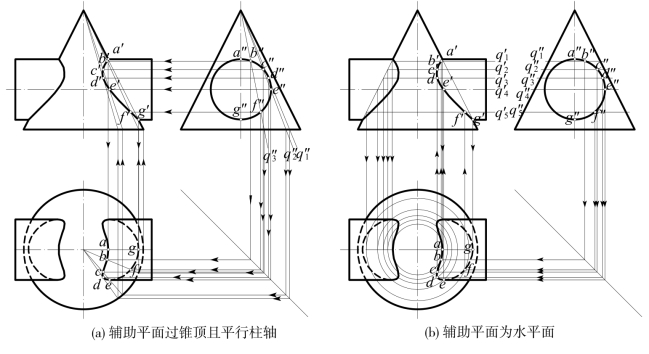
图8-27　圆锥与圆柱相贯

因圆柱面垂直W面，故相贯线的W面投影与圆柱面的积聚投影重合，现只需求相贯线的H面和V面投影。

（2）相贯点作法：首先，过圆锥和圆柱的轴线作V面平行面为辅助平面，它与锥面、柱面的截交线为V面的投影外形线（最左、最右素线及最高、最低素线），四根截交线间有四个交点（本题只作出右侧的两个交点A，G）。

至于其他相贯点，可用如下两种辅助平面来作出：

方法一：如图8-27（a），辅助平面过锥顶且平行柱轴，并垂直W面，与锥面、柱面各交于直素线，直素线间的交点即为相贯点。本题中与柱面的W面积聚投影相切的辅助平面Q1、通过柱面最前素线的辅助平面Q2必须作出，另外再作一些如Q3的辅助平面，应用这些辅助平面可得一系列相贯点。图中可通过柱面和辅助平面的积聚投影先求出相贯点的W面投影，再求出H面、V面投影。如由切点d″通过锥面上取点法（素线法）求出d，d′。

方法二：如图8-27（b），辅助平面为H面平行面，由于它垂直锥轴并平行柱轴，必与锥面、柱面分别交得水平的纬圆和直素线，它们间的交点即为相贯点。本题中各相贯点的W面投影已知（在柱面的积聚投影上），通过向H面作连系线，与各水平辅助平面（Q1，Q2…）交得的纬圆相交，即为各相贯点的H面投影，再向上作连系线得各相贯点的V面投影。

本题只作出了右前方一系列相贯点的投影，根据对称性可作出右后方及左方的相贯点投影，最后顺次相连。

（3）可见性：相贯线的V面投影，是前方可见的和后方不可见的重影，故仍画成实线；H面投影中，锥面的投影都可见，故只有位于圆柱面下半部不可见的H面投影画成虚线，E是可见和不可见的分界点。