双曲线的画法及特性-画法几何（第6版）

1.双曲线的形成

平面内一动点E1到两定点F1，F2的距离差为定长2a时，形成一条双曲线K，如图7-19所示。F1，F2称为焦点，距离F1F2=2c称为焦距。

双曲线的一种作法——由焦点作双曲线：取一个长度r，分别以r和2a+r为半径，以F1，F2为圆心作圆弧，可交双曲线K上E1，E2，E3和E4四点。同法，取一些长度r，可作许多点来连得双曲线K。

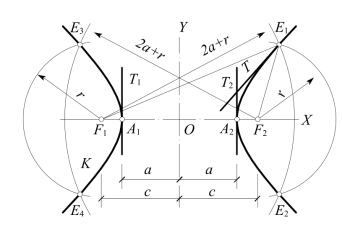
图7-19　双曲线及其切线

图7-20　双曲线的渐近线

当r=c-a，即以半径c-a和2a+r=a+c作圆弧时，仅能作得K上两点A1，A2；当r无限增长时，K也无限延伸。

由于点E1与E2，E3与E4对称于一直线X，又E1与E3，E2与E4对称于另一直线Y，故双曲线K有X和Y两条轴。X与K相交，称为实轴；Y与K不交，称为虚轴。K与X的交点即点A1、A2，称为双曲线的顶点。A1A2=2a，称为顶点距。两轴的交点O，为E1与E4，E2与E3的对称点，故为K的对称中心，称为双曲线的中心，也为F1F2，A1A2的中点。

2.双曲线的切线

（1）由焦点作双曲线的切线——如图7-19，以双曲线上任一点E1为切点，作双曲线的切线T：连线E1F1，E1F2，作∠F1E1F2的平分线，即为双曲线于点E1处的切线T。

双曲线K于顶点A1，A2的切线T1，T2，称为双曲线的顶点切线，T1，T2均垂直于实轴X。

（2）渐近线——切双曲线于无限远点的直线，称为渐近线，因双曲线对称于X、Y轴，故渐近线有两支，如图7-20中直线U1，U2，并交于中心点O和对称于X、Y轴。

双曲线的渐近线U1，U2，与顶点切线T1，T2，以及由焦距F1F2为直径的称为焦点圆的圆周，交于四点如B1，B2…等，如图7-20所示。于是，如已知渐近线、顶点和焦点三种中的任两种时，即可作出另一种。

渐近线作法：双曲线上点、渐近线上点和顶点到Y轴的距离，即e，d，a，将构成一个直角三角形。（如图7-20所示，过双曲线K上一点如E，由之作Y轴垂线，与渐近线U1，Y轴各交于D，G点，设取e=EG，d=DG和OA1=a。于是以OA1=a为一直角边，在Y上取d为另一直角边，斜边=e，即构成一个直角三角形。）于是，如已知双曲线，过点E作Y轴的垂线EG，得长度e。于是以A1为圆心，e为半径作圆弧，与Y轴交得点¯D，得出长度d。于是在EG上取长度DG=d，就可作得渐近线U1。作U1的对称于轴X的直线，即为渐近线U2。

3.双曲线的弦和直径

（1）弦——双曲线上任两点的连线，称为双曲线的弦。如图7-21所示的弦E1E2，E3E4。

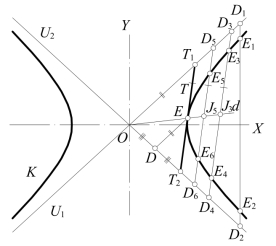
（2）直径——双曲线上平行弦的中点连线，必过双曲线的中心，称为双曲线的直径。如图7-21中过平行弦E3E4、E5E6中点J3，J5的直径d通过双曲线的中心O。

（3）双曲线弦上介于双曲线和渐近线间两线段的长度相等——如图7-21中，弦E1E2垂直X轴，由于对称关系，很明显地E1D1=E2D2。当弦E3E4倾斜时，E3D3=E4D4（证略）。

（4）通过弦线中点的直径与双曲线交点处的切线，平行于这些弦，该交点成为切点，且切点为切线位于与渐近线内长度的中点。因为，如图7-21中的弦E3E4，使其中点J3沿着直径d作平行移动，当J3经过E5E6的中点J5而到达直径d与双曲线K的交点E时，点E3，E4也在K上经过E5，E6而趋近于点E。因而E3E4成为K于点E的切线T。E3E4与渐近线U1，U2的交点D3，D4，则U1，U2上到达切线T与U1，U2的交点T1，T2，而点E成T1T2的中点。

(www.xing528.com)

图7-21　双曲线的弦线、直径和切线

（5）已知双曲线的渐近线求双曲线上一点的切线——如图7-21中，设过点E作ED∥U1，因ET1=ET2，故ED与U2的交点D，为OT2的中点。故已知U1，U2，求点E的切线，可作ED∥U1，与U2交于点D。再在U2上量DT2=DO，得T2点。则连线T2E即为所求切线T。

4.弦线法作双曲线

已知渐近线U1，U2及双曲线上任一点E作双曲线K，见图7-22。

由于双曲线上一弦介于双曲线和渐近线间线段等长，故过点E作许多弦如12，34，…。与U1，U2交于1，2和3，4等点，取点如E1，使E12=E1；又取E2，使E24=E3，…，于是得出E1，E2，…许多点，即可连得双曲线K。

已知双曲线的两点、一轴和两条渐近线的方向，作双曲线的中心和渐近线——如图7-23所示，如已知渐近线U1、U2，由两已知点E1，E2作U1，U2的平行线，构成一平行四边形O1E1O2E2。对角线O1O2平分另一对角线的弦线E1E2，中点为J。又设弦线E1E2交渐近线U1于点D1。则△JE1O1∽△JD1O。因J，E1，D1共线，故JO1O也共线。

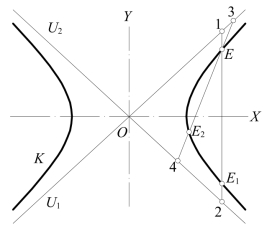
图7-22　弦线法作双曲线

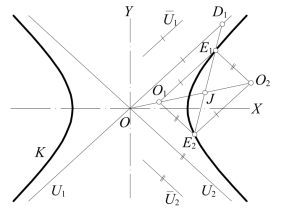
图7-23　由渐近线的方向等作双曲线的中心和渐近线

于是，设已知平行于渐近线的方向线，实轴（或虚轴）和两点E1，E2。先定出弦线E1E2的中点J；并由E1、E2作¯U1，¯U2的平行线，得交点如O1。则连线JO1与实轴（或虚轴）交得中心O；由之即可作出渐近线。于是可由弦线法作出双曲线。

5.双曲线的投影

双曲线平面平行或垂直于投影面时，双曲线的投影分别反映实形和积聚成直线；一般情况下，双曲线的投影仍是双曲线，渐近线的投影是投影双曲线的渐近线。当双曲线的任一轴线为投影面的平行线时，实轴、虚轴的投影仍分别是投影双曲线的实轴和虚轴。

现将图7-22中的双曲线连同两条渐近线及许多弦线作投影。由于直线上两等长线段的投影仍相等，故一条弦线上介于双曲线和渐近线间的两线段投影长度仍相等。也就是根据双曲线上一点的投影及两条渐近线的投影，可作出双曲线的投影。既然图7-22中的曲线是双曲线，故采用同样方式作出的投影曲线也必是双曲线，且渐近线的投影为投影双曲线的渐近线。

实际作图时，只要作两条渐近线的投影和双曲线上一点的投影，即可在投影中用弦线法作出投影双曲线。

当轴线之一平行投影面时，两轴线的投影仍互相垂直，即投影双曲线对它们的对称性也不变，故它们也为投影双曲线的实轴和虚轴。

[例7-2] 图7-24所示为空间一般位置平面上一条双曲线K的一支的V面投影和W面投影。设先作出双曲线上一对渐近线U1，U2和任一点A的投影，就可应用图7-22的方法，作出K的投影k′，k″。两条渐近线的交点O，即为双曲线的中心的投影，故投影o′，o″位于同一条连系线上。

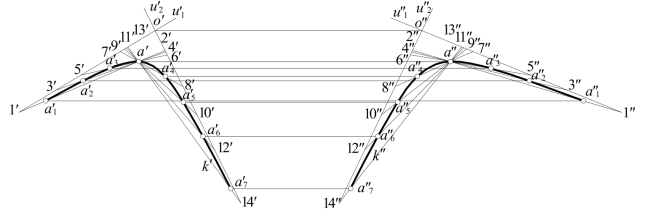
图7-24　双曲线一支的投影图