画抛物线的方法与步骤

1.抛物线的形成

平面内一动点E1到一个定点F和到一条定直线L的距离相等时（E1F=E1G1），形成一条抛物线K，如图7-15所示，F称为焦点，L称为准线。F到L的距离用字母p表示。于是得：

抛物线的一种作法——由焦点和准线作抛物线：

如图7-15所示，任取一个长度r，以焦点F为圆心，以r为半径作圆弧，与距准线L为r的平行线的交点E1，E2为抛物线K上两点。同法，取一些长度r，可作出许多点来连得抛物线K。

当r=p/2时，只能作出一点A；当r无限增大时，K的两端也无限延伸。

因E1和E2对称于AF，故K对称于直线AF，AF为通过焦点F而垂直于准线L的直线，称为抛物线的轴，常用字母X来表示。轴X与K的交点即为点A，称为抛物线的顶点。且A为FG的中点。

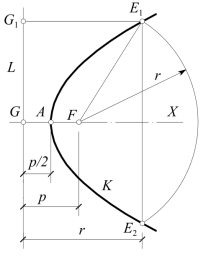
图7-15　抛物线

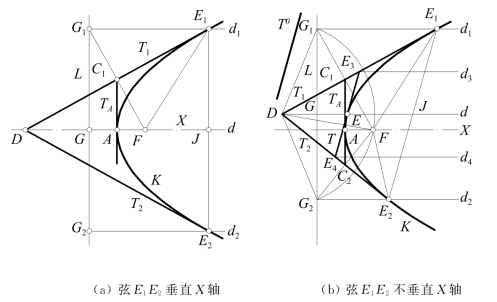
图7-16　抛物线的弦、直径和切线

抛物线上任两点的连线，称为抛物线的弦，如图7-16所示。图（a）的弦E1E2垂直于轴X，垂足J为E1E2的中点；图（b）的弦E1E2倾斜于轴X。

过抛物线上任一点平行于轴X的直线，或各平行弦中点的连线，称为抛物线的直径。如图7-16（a）中通过K上点A，E1，E2的直径d，d1和d2。本图中，d与X重合，d1，d2与由E1，E2向L所引的垂线E1G1，E2G2重合。

2.抛物线的切线

（1）由焦点和准线作抛物线的切线——如图7-16（a）所示，过E1作K的切线T1：作∠FE1G1的平分线即为切线T1。

抛物线K于顶点A的切线TA，称为顶点切线，垂直于轴X。

（2）由焦点、轴X作抛物线的切线——如图7-16（a），设已经用前法作出抛物线K于点E1的切线T1，因E1F=E1G1，则△E1FG1为等腰三角形，且切线T1为∠E1的平分线，也为三角形的中线，且垂直于底边FG1，故垂足C1为FG1的中点。因顶点A为FG的中点，故点C1位于顶点切线TA上。

再设延长切线T1与轴X交于点D，由于△DFC1≌△E1G1C1≌△E1FC1，故FD=FE1。于是：在X上量取FD=FE1，得点D；连线DE1即为K于点E1处的切线T1。由于E1和E2对称于轴X，故连线DE2为K于E2点的切线T2。

（3）由顶点、轴X作抛物线的切线——如图7-16（a）所示，由点E1向轴X引垂线，垂足为点J。如已作出点D，则在△E1DJ中，由于E1C1=C1D，故C1为DE1的中点，因而顶点A为DJ的中点，于是：

在X上量取AD=AJ，得点D，连线DE1即为K于E1处的切线T1。

（4）斜弦两端的抛物线切线作法——如图7-16（b）所示。设抛物线K于点E1，E2的切线T1，T2已利用焦点F和准线L作出，相交于一点D。因D位于∠E1，∠E2的平分线T1，T2上，且F与G1，F与G2分别对称于T1，T2，所以DG1=DF=DG2，故过点D的直径d与L的交点G为G1G2的中点。因而直径d与直径d1，d2等距，即d与E1E2的交点J为E1E2的中点。

现设E1E2沿着直径方向作平行移动。当J到达d与K的交点E处时，则E1，E2在K上无限接近于E点，E1E2成为K于E点处的切线T。

又设想E1，E2分别沿着切线T1，T2到达点E3，E4。再过E3，E4作直径d3，d4。由于E3，E4分别为切线T1与T，T2与T的交点，故按上述，d3，d4也分别与d和d1，d和d2等距。因而这些直径之间的距离均相等，故E为E3E4的中点；E3，E4就分别为DE1，DE2的中点。由之并可得出E为DJ的中点，如图7-16所示。于是：(www.xing528.com)

①K上斜弦E1E2的两端的切线T1，T2的作法：过E1E2的中点J作直径d，与K交于点E。再在d上量ED=EJ，得点D。连线DE1，DE2即为切线T1，T2。

②E处切线T为DE1，DE2中点E3、E4的连线。

（5）作切线平行于已知直线T0：如图7-16（b）所示，作弦线E1E2平行T0，取中点J，作直径d∥X，如X未作出，则取两条平行弦的中点连得d与K的交点E即为切点。过E作T0的平行线T，即为所求切线。

从图中可以看出，抛物线K也为切线T1，T和T2的包络线，切点为E1，E和E2。

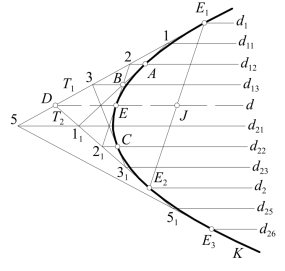
图7-17　包络线法作抛物线

3.包络线法作抛物线

设有一抛物线K上两点E1，E2和切线T1，T2，求作K，如图7-17所示。

设利用上述作法，作出许多切线，并定出切点来作出抛物线，步骤如下：

设切线T1，T2交于点D，先将DE1，DE2作同数等分，再将分点编号。如图7-17所示，将编号次序相同的点作连线111，221，…，即为K的切线。其切点为每条切线与相邻两切线的交点间线段的中点，如点A为1B的中点。并作出通过各点的直径d1，d11，…等，它们的距离必相同。于是作切于各切线的切点处的包络线，即为所求抛物线K。实际作图时，各直径不必作出。

4.作抛物线的延长线

图7-17中，在T1，T2的延长线上，取等分点5，51，并作出直径d25，d26，则可作出K的延伸线，与连线551切于551与d26的交点E3处。

5.抛物线的投影

抛物线平面平行或垂直于投影面时，抛物线的投影分别反映实形和积聚成一直线；一般情况下，抛物线的投影仍是一条抛物线。当轴线为投影面的平行线或为最大斜度线时，则轴线的投影为投影抛物线的轴线。

如前所述，当已知抛物线上两点及其切线时，可用图7-17的方法，用包络线法作出抛物线。现设想将图7-17中抛物线的两点、两条切线，作图过程中的等分点以及它们连成的切线和切点等，随同抛物线一起作投影。由于直线和曲线的相切、相连、平行和等分等性质，在投影中均不变，即投影曲线也必切于原来切线的投影等。既然用图7-17的方法作出的曲线肯定是一条抛物线，故具有同样方式形成的投影曲线也必是一条抛物线。

包络线法作抛物线的投影抛物线——实际作图时不必作出原来所有切线的投影，只要作出两点连同两条切线的投影，即可在投影中用包络线法作出投影抛物线。

当抛物线的轴为某投影面平行线或最大斜度线时，垂直于轴的对称弦的投影，仍必垂直于轴的投影，抛物线的投影仍对称于轴的投影，即轴的投影为投影抛物线的轴。

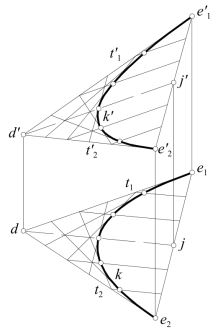
图7-18　抛物线的投影图

[例7-1] 如图7-18，为空间一般位置平面上一条抛物线K的投影图。设先作出K上两点E1、E2和两条切线T1、T2的投影，就可应用图7-17的方法，作出K的投影k和k′。两条切线的交点D的投影，为两条切线的投影的交点d、d′，故位于同一条连系线上。