椭圆的共轭直径及求长、短轴方法

1.椭圆的形成

椭圆除了圆周平面倾斜于投影面时形成之外，可由各种情况形成。几何学中，椭圆的一种形成如下：

如图7-8所示，平面内一动点E1到两个定点F1，F2的距离E1F1，E1F2之和为定长2a时，形成一个椭圆。F1，F2称为焦点，距离F1F2=2c，称为焦距，定长2a将为长轴的长度。

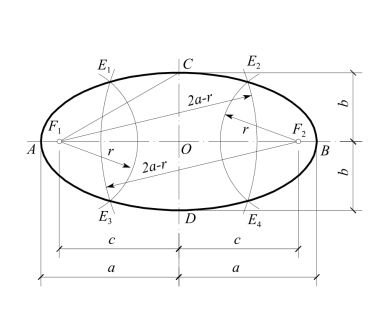
图7-8　椭圆的形成

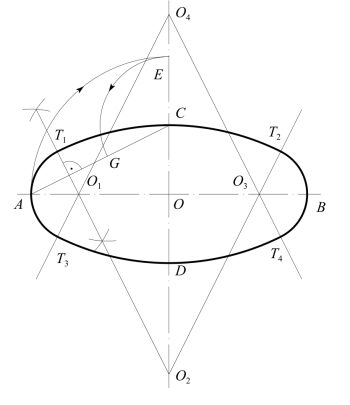
图7-9　四圆弧近似法作椭圆

（1）椭圆的一种作法——由焦点作椭图：取一个长度r，分别以r和2a-r为半径，F1和F2为圆心作圆弧，可交得椭圆上四点E1、E2、E3和E4。同法，取一些长度r，可作得许多点来连得椭圆。

当长度r=a-c和2a-r=a+c为半径作圆弧时，则仅能交得位于F1F2线上两点A和B，AB即为长轴，故AB=2a。当长度r=a和2a-r=a为半径作圆弧时，也仅能交得两点C和D，连线CD即为短轴，长度CD用2b表示。

（2）由长短轴定焦点——如已知椭圆的长短轴AB和CD，以短轴顶点C或D为圆心，以长轴的一半长度，即取为为半径作圆弧，即可在AB上作得焦点F1和F2，再用前法作出椭圆。

2.四圆弧近似法作椭圆

已知椭圆的长短轴，可有各种方法作出一些点来连成椭圆，如图7-8所示，由长短轴求出焦点后准确地作出椭圆，但一般较繁。工程图上一般作出近似的椭圆形即可，现介绍以四个圆弧来近似地表示一个椭圆的方法（证略）。

如图7-9所示，已知长短轴AB，CD，作图步骤如下：①先在CD的延长线上，取OE=OA；②再在连线AC上，取CG=CE；③作AG的中垂线，交两轴于O1，O2点；并在AB，CD上，取OO3=OO1，OO4=OO2；④分别以O1，O2，…为圆心，至相应的轴线顶点的距离O1A，O2C，O3B和O4D为半径作四个圆弧，即可组成一个近似椭圆。各圆弧相切于相应的圆心连线O1O2…上的T1，T2，T3和T4四点。

3.椭圆的共轭直径

（1）圆周上一对互相垂直的直径的投影，称为椭圆的一对共轭直径。又椭圆的两条直径中，当一条直径能平分另一条直径的平行弦时，则这两条直径是一对共轭直径。又椭圆的两条直径中，当一条直径能平行另一条直径端点的椭圆切线时，这两条直径同样也是一对共轭直径。

如图7-10（a）所示，圆周K1有一对互相垂直的直径E1F1和G1J1，并有任一弦M1N1平行E1F1，必被G1J1平分。又过E1F1和G1J1的端点作圆周的切线，则每条切线平行于另一条直径，于是这四条切线组成了一个正方形。

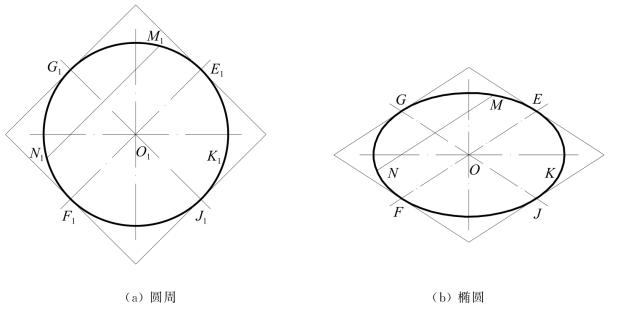
图7-10　椭圆的共轭直径

在图7-10（b）中，设椭圆K是图7-10（a）中圆周K1的投影。K上直径EF，GJ和弦MN分别为K1的E1F1，G1J1和弦M1N1的投影。EF和GJ成为椭圆的共轭直径。由于作投影时，直线的平行、分比和曲线的切线等性质不变，故得上述的一些结论。

不过，由于直角的投影一般不再成为直角，故椭圆的一对共轭直径一般不垂直，即圆周的外切正方形一般成为椭圆的外切平行四边形。特别情况下，当椭圆的一对共轭直径互相垂直时，则成为椭圆的长、短轴。

（2）由椭圆共轭直径求长、短轴——如图7-11所示，已知椭圆的一对共轭直径EF和GJ，其交点O为椭圆心，求椭圆的长、短轴（证略）。

如先由O作OG0⊥OG，且使OG0=OG。并以连线EG0的中点S为圆心、SO为半径作半圆，与EG0的延长线交于点M，N。于是连线OM，ON分别为长、短轴的位置线。然后在OM上量取OA=OB=G0M或=EN，以及在ON上量取OC=OD=G0N或=EM，则AB和CD就是椭圆的长、短轴。

（3）已知椭圆上一点和长、短轴之一，求另一轴——由图7-11可引出图7-12，即在图7-12中，如已知点E和长轴AB，求CD。

首先，作AB的中垂线，必为短轴的位置线，垂足为椭圆心O。再以点E为圆心，长半轴长度为半径作圆弧，与短轴位置线交于点N或N1。作连线EN或EN1，与长轴AB交于点M或点M1。则连线EM或EM1的长度等于短半轴长度b，于是由点O量取OC=OD=b，即得短轴CD。(www.xing528.com)

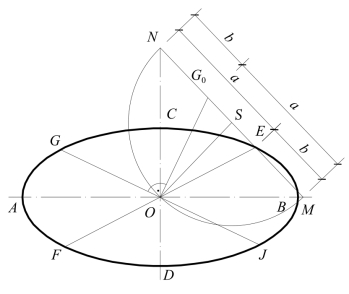
图7-11　由椭圆的共轭直径求长、短轴

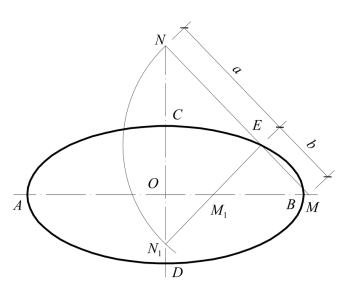
图7-12　已知椭圆上的一点及一轴求另一轴

同样，由图7-12可知，如已知点E及短轴CD，也可作出长轴AB。

4.椭圆的切线

（1）由焦点作椭圆切线——见图7-13（a），已知椭圆K的焦点F1，F2，以椭圆上一点E为切点，作椭圆的切线，作法如下：作连线EF1，EF2，再作夹角F1EF2补角的平分线，即为椭圆于E点的切线T（证略）。

图7-13　椭圆的切线作法

（2）由共轭轴作椭圆切线——见图7-13（b），已知椭圆K和K上一点E，以E为切点作切线。

根据图7-13（b），过点E作直径EOF。再作其平行弦如MN，取中点G0，作连线OG0，与K交得EF的共轭直径GJ。于是由点E作GJ的平行线T1，即为K于点E的切线。

（3）作椭圆切线平行于已知直线——见图7-13（b），已知椭圆K和直线L，作平行L的椭圆切线T2及定出切点G。

作椭圆切线如T2平行L，可利用三角板可推平行线，本题的关键是准确地定出切点G的位置。可作平行于L的椭圆弦如EF，MN，取它们中点O，G0作连线，与K的交点G即为切点。

5.椭圆的投影

（1）椭圆平行于投影面时，其投影是一个等大的椭圆。

（2）当椭圆平面垂直于投影面时，其投影是一条直线，长度相当于椭圆上与投射线共轭的一条直径的投影长度。

（3）当椭圆平面倾斜于投影面时，椭圆的投影仍是一个椭圆。椭圆的一对长、短轴的投影，成为投影椭圆的一对共轭直径；但当长轴平行于投影面时，长、短轴的投影仍分别为投影椭圆的长、短轴；又当短轴平行于投影面时，长、短轴的投影可以互换，甚至相等，此时，当长、短轴的投影长度相等时，投影椭圆成为一个圆周。一般情况下，椭圆的一对共轭直径的投影仍成为投影椭圆的一对共轭直径。

图7-14（a）为一个椭圆K，设K及其一对共轭直径GJ，EF及平行弦MN的投影为k，gj，ef和mn，如图7-14（b）所示。此时，mn仍平行ef，端点m，n在k上，且其中点在gj上，即它们之间的位置、距离和长度之比等仍保持不变。k的这些性质完全相同于K的性质，可见k也是一个椭圆。其实，此时的k，也相当于空间一个圆周的投影。该圆周的直径长度，等于投影椭圆k长轴的长度。

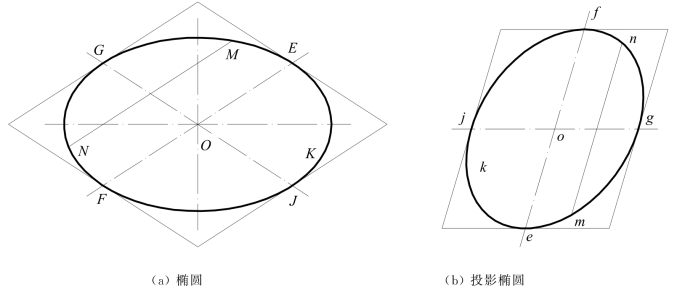
图7-14　椭圆的投影图

由于椭圆投射成投影椭圆k的过程中，曲线的切线性质不变，故椭圆K的长、短轴和每对共轭直径的投影，将是k的共轭直径。只有K的一对共轭直径的投影互相垂直时，才能成为k的一对长、短轴；或者k的长、短轴之一平行于投影面时，由于此时直角的投影仍是直角，因而长、短轴的投影仍成为投影椭圆的长、短轴。

由上所述，圆周的投影可为圆周或椭圆，椭圆的投影也可为圆周或椭圆。实际上，圆周为椭圆的所有直径相等时的特殊情况。