画法几何（第6版）：圆周投影及椭圆绘制方法

1.投影面平行面上圆周的投影

圆周平行于投影面时，其投影是一个等大的圆周；圆周平面垂直于投影面时，其投影积聚成长度为圆周直径的一段直线。

图7-5（a）（b）（c）是分别平行于H，V，W投影面的圆周K，L，M的投影图，在H，V，W面上的投影为反映实形的圆周，在其他投影面上的投影积聚成长度为直径的直线，呈水平或竖直方向。

在投影图上，圆周的投影为圆周时，应当用细单点长画线表示圆周上一对互相垂直的对称位置线，称为圆周的中心线，两端稍伸出圆周2～3mm。

2.投影面垂直面上圆周的投影

圆周平面倾斜于投影面时，其投影为一个椭圆。圆心的投影为投影椭圆心。圆周直径的投影为投影椭圆的直径。圆周内平行于该投影面的直径的投影，为投影椭圆的长轴，长度等于圆周直径；圆周内与该直径垂直的那条直径的投影，为投影椭圆的短轴。

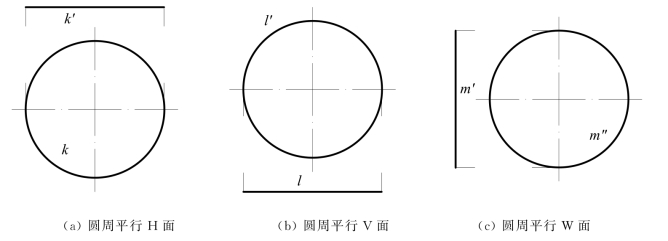
图7-5　圆周平面平行投影面

（1）投影面垂直面上圆周的投影——如图7-6（a）所示，圆周K位于W面垂直面P上，它的W面投影k″积聚成一直线，相当于K上平行W面的直径CD的投影c″d″，长度等于CD。

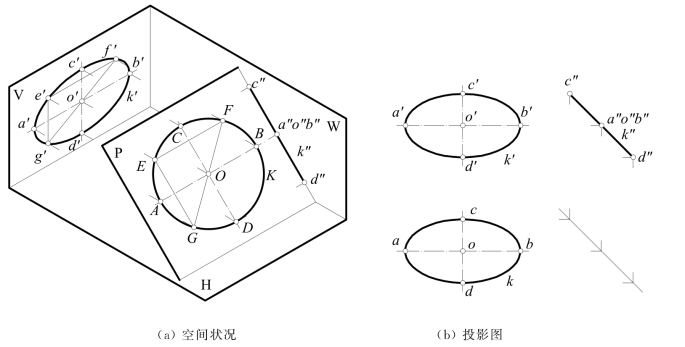
图7-6　圆周平面垂直投影面

P面倾斜于V面，圆周K的V面投影k′的形状为椭圆，真实形状如图7-6（b）中V面投影k′所示。K内任一直径如FG的V面投影为f′g′，端点f′和g′在k′上。圆心O的V面投影o′为f′g′的中点，故o′成为k′的对称中心，成为椭圆心，f′g′成为椭圆的直径。

圆周上各条直径虽然长度相等，但由于它们对V面的倾角不同，投影的长度也就不同，一般都为缩短。只有平行于V面的那条直径AB的投影a′b′的长度不变而最长，为投影椭圆的长轴。又垂直于AB的那条圆周直径CD，因位于对V面的最大斜度线上，故c′d′缩得最短，成为投影椭圆的短轴。而且长、短轴a′b′和c′d′互相垂直。长、短轴的端点a′，b′，c′和d′称为椭圆的顶点。利用平行于AB和CD的圆周弦线EF和EG的投影e′f′，e′g′分别对称于a′b′，c′d′，故整个椭圆k′必将以长、短轴a′b′，c′d′为对称轴。(www.xing528.com)

图7-6　（b）中，圆周K的H面投影k也为一个椭圆，因圆周直径AB和CD又分别为H面的平行线和最大斜度线，故投影ab，cd又分别为k的长、短轴。但由于CD对V面和H面的倾角不同，故cd的长度和c′d′的长度也是不同的。

已知椭圆的长、短轴，即可作出椭圆，将在后述。

（2）一般位置平面上圆周的投影——见图7-7，已知一平面EFGH的两面投影；并设平面上有一圆周直径长度为D，如图旁直线段所示；设已知圆心O的投影，求作圆周的投影。

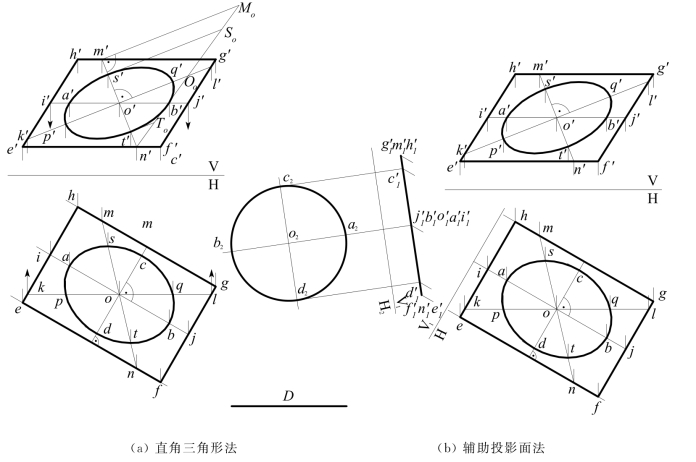
图7-7　圆周平面为一般位置平面

因圆周平面为一般位置，对各个投影面均呈倾斜，故圆周的各面投影均为椭圆。如能求出投影椭圆的长、短轴，即可作出椭圆。

H面、V面投影椭圆长轴分别为圆周上H面、V面平行线上直径的投影，长度为D。故如图所示，利用平面上过圆心O的H面平行线IJ和V面平行线KL，并在上面以o和o′为中点，分别作长度ab=D和p′q′=D，得长轴顶点a，b和p′，q′。

至于短轴方向，分别在过o和o′的ab，p′q′的垂线上，短轴的顶点c，d和s′，t′的位置，可由各种方法作出，现介绍下列三种方法：

①利用直角三角形法求直线上点的方法：如在V面投影上，求MN的实长n′M0，并以O0为中点，取S0T0=D，定出s′t′，即V面投影椭圆的短轴。同法，可求出H面投影椭圆的短轴cd。

②利用辅助投影面法：先把圆周所在的平面EFGH变成V1面的垂直面，再变成H2面的平行面，则圆周在H2上反映实形，从H2返回到H，可求出H面投影椭圆的短轴cd。同法，可求出V面投影椭圆的短轴s′t′。

③利用椭圆的一轴和椭圆上一点求另一轴的方法：例如：在图7-7的H面投影上，已知椭圆的长轴ab，并知对应于V面投影椭圆上长轴顶点p′，q′的H面投影点p，q，于是可应用图7-12的方法，求出短轴顶点c，d（图7-7中作图线略）。同样，可作出V面投影椭圆的短轴。

长、短轴求得后，就可应用图7-8或图7-9的方法作出椭圆或近似椭圆。