同坡屋顶的H面投影与V面投影

1.同坡屋顶

对水平面倾角相同，且房屋四周屋檐高度相同的屋面所构成的屋顶，称为同坡屋顶。已知同坡屋顶屋檐的H面投影和屋面的倾角，求作屋面间交线来完成同坡屋顶的投影图。可视为特殊形式的平面立体相贯。

2.屋面交线的投影特性

（1）屋檐平行的两屋面必交成水平的屋脊，称为平脊。它的H面投影，必平行于屋檐的H面投影，且与两屋檐的H面投影等距。如图6-23所示，屋面P和Q所交成的平脊B的H面投影b，平行屋檐C，D的H面投影c，d，且与c，d等距。因为由V面投影可知，，故，即为c′d′的中点，故b与c，d等距。

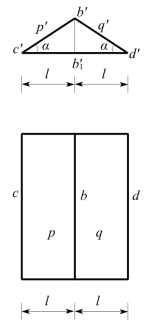
图6-23　两坡屋顶

图6-24　四坡屋顶

（2）屋檐相交的两屋面必相交成倾斜的屋脊或天沟，称为斜脊或斜沟。其H面投影为两屋檐H面投影的夹角平分线。如图6-24所示为屋顶形成H面投影时的情况，屋面P和Q的屋檐交于A点，则交线AB必通过该点。设交线上有任一点B，向每条屋檐作垂线，即在每个屋面上作最大斜度线，BE⊥AE和BF⊥AF；又自点B作屋檐平面的垂线，得垂足B1。B1相当于点B在屋檐平面上的正投影。故B1E⊥AE，B1F⊥AF，BE、BF的倾角即为屋面的倾角α。由于直角三角形△BB1E≌△BB1F，因它们公有一直角边BB1，且∠E=∠F=α，故B1E=B1F。于是具有同一条斜边AB1的△B1AE≌△B1AF，因而∠B1AE=∠B1AF。即在H面投影中，∠bae=∠baf，故交线的H面投影ab为两屋檐H面投影eaf的夹角平分线。

（3）屋顶上如有两条交线交于一点，至少还有第三条交线通过该交点。仍如图6-24所示，设P和R两屋面的交线BG，与P和Q两屋面的交线AB交于一点B，则点B必为P，Q，R三面的交点，故也为Q，R两屋面交线上的一点，即Q，R屋面的交线BJ应通过点B。

3.求作同坡屋顶投影的步骤

（1）先根据屋檐的H面投影，按交线的投影特性，求出交线的H面投影，即完成同坡屋顶的H面投影。(www.xing528.com)

（2）再根据屋檐的V面投影高度、屋面的倾角，由屋顶的H面投影，完成屋顶的V面投影。

[例6-18] 如图6-25所示，已知同坡屋顶四周屋檐的H面投影，以及屋面的倾角α，完成同坡屋顶的H面投影和屋檐呈水平线的V面投影。

图6-25　同坡屋顶

[解] （1）H面投影作法：要完成屋顶的H面投影，即求作屋面交线的H面投影，为使作图较有规律，特采用屋面编号的方法。作图步骤如下：

①在H面投影中，将屋面编号，如图6-25（b）中的1，2，…，8等。

②作各相交屋檐的角平分线，并用有关两屋面（檐）的编号来表示，如编号为1，2屋面交线的H面投影用12表示，于是得12，23，…，18等；

③同时由屋顶的端部开始，作出左端12和18的交点a，右端45和56的交点b，如图6-25（c）所示，再分别作出通过a，b的第三条交线。该第三条交线再与它首先相交的另一交线，可交得新的交点和通过该点的第三条新的交线，直到每一屋面成为一个闭合的多边形为止。

设以点a为例，通过点a的第三条交线应该是28（可从交线编号12、18除去共有的1，即得28），交线28应是编号为2和8的屋面交线，为与屋檐2和8平行的等距线。再自a所作的屋脊28，前进中首先相交的是已经作出的交线78，得交点c，则通过c的第三条交线必是27（由28，78中除去共有的8），为屋檐2，7的夹角平分线。而27先与交线23交于点e，又有第三条交线37通过点e。以同样的方法，可依次作出所有交线的H面投影。此时，每一屋面的H面投影必呈闭合形状，即为同坡屋顶的H面投影。

（2）V面投影：在水平方向屋檐的V面投影上方，作屋面及交线的V面投影。

作图时，首先从垂直于V面的屋面着手，因为它们的积聚投影能反映屋面的倾角α；再画出与相邻屋面交线（如屋脊等交线）的V面投影。以同样方法依次作出所有交线的V面投影并判别可见性，即得每个屋面的V面投影，于是完成整个同坡屋顶的V面投影。