画法几何（第6版）：棱柱和棱锥的截断实例

[例6-11] 如图6-14所示，求直三棱柱ABC与一般位置平面△DEF相交时的截交线投影。

[解] （1）截交线形状分析：在H面投影中，三棱柱投影△abc位于截平面投影△def的范围内；在V面投影中，三棱柱顶、底面投影伸出△d′e′f′。故△DEF仅与三棱柱的三个侧面相交，截交线是△A0B0C0。其中截交点A0、B0、C0是三棱柱的三条侧棱A、B、C与△DEF的交点；截交线段是三棱柱的三个侧面与△DEF的交线。

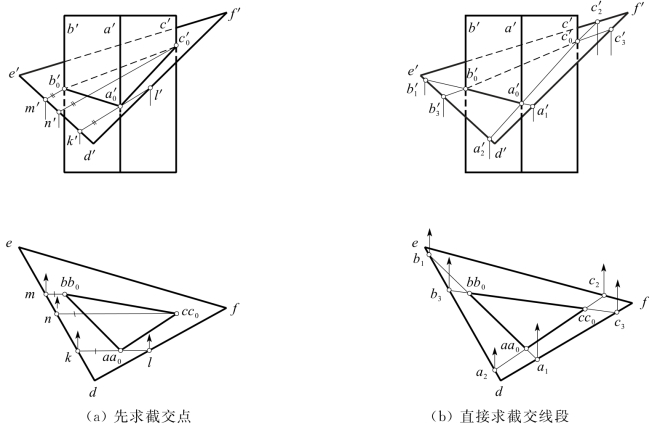
图6-14　三棱柱的截断

（2）截交线H面投影：因三棱柱的三个侧面均垂直H面，故它们的H面投影具有积聚性，即截交线的H面投影与这些积聚投影重合。

（3）截交线的V面投影求法：

方法一：利用棱线的积聚性——即先求截交点，再连成截交线。如图6-14（a）所示因截交点A0的H面投影a0必在棱线A的积聚投影a上，于是成为在△DEF上由a0求的问题。现通过A0在△DEF上取一条辅助线，先作出其H面投影kl，与△def的边线交于点k和l，求出k′和l′后的连线k′l′与a′交得同法，过b0和c0作辅助线的H面投影，本图中，如所作的b0m∥c0n∥kl，只要由m和n求出m′和n′后，作来交得于是可连得

方法二：利用棱面的积聚性——即直接求出各截交线段来组成截交线。如图6-14（b）所示，因截交线△A0B0C0的H面投影必积聚在△abc上，故把位于△DEF上的截交线段A0B0的H面投影a0b0延长，与△def的边交于点a1和b1，则求出后的连线与a′和b′交得A0B0的V面投影。同法，求出。实际上，只要求后，即可连得

（4）可见性：仅V面投影需要判断。因A0B0、A0C0分别位于可见棱面AB及AC上而可见，故画成实线；又因B0C0位于后方不可见棱面BC上而不可见，故画成虚线。另外，A，B，C三条棱线及△DEF的三条边线在对方投影的边框范围内部分也要判定可见性。

[例6-12] 如图6-15所示，求三棱锥被V面垂直面P（PV）截断后下半部分的投影、截断面实形和表面展开图。

[解] （1）截交线形状分析：图6-15（a），因PV与s′b′和s′c′及底面的V面投影a′b′c′相交，可知P面与三个棱面和一个底面相交成一个四边形，但不与棱线SA和底边BC相交。

（2）截交线投影求法：因PV有积聚性，故截交线的V面投影必在PV上而为已知，即截交点B0，C0，D0和E0的V面投影可直接定出。

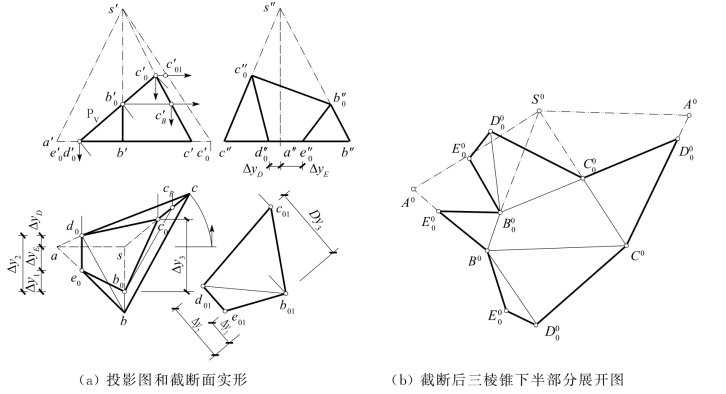
图6-15　平面与三棱锥的截断和展开

然后按照直线上点的投影作法，可求出各截交点的H面及W面投影，如图所示。其中b0可利用△SBC上一条水平辅助线B0CB来求出。即由作水平线，由求出cB，再作cBb0∥cb，与sb交得b0。也可由作水平连系线与s″b″交得，由求b0；至于，可由，d0和，e0作出。也可利用D0和E0与点A的坐标差ΔyD，ΔyE来作出。

棱锥上半部因为已截去，在图中可用细双点画线来表示。因截交线B0C0D0E0B0位于立体下半部分的左上方，故H面、W面投影均用实线表示为可见的。(www.xing528.com)

（3）截断面实形：反映截断面实形的四边形b01c01d01e01，可用辅助投影面法作出。为了省略作出O1X1∥PV，故在过且垂直于PV的直线上取任一点如b01，再由坐标差Δy1，Δy2，Δy3，作出e01，d01，c01后相连而成。

（4）展开图：三棱锥截断后下半部分的表面展开图，如图6-15（b）所示。首先参考图6-8，作出完整三棱锥表面的展开图S0A0B0C0，其中长度S0A0=s′a′，S0B0=s″b″，S0C0等于SC旋转到平行V面后的长度。然后作出截交点在展开图中的位置，它们都可由反映棱线实长的投影中取长度来定出。例如，可由作水平线（因C0随同SC旋转时，旋转圆周的V面投影成水平方向），与交得，则量取来得出。最后作各截交点展开位置的连线，并加上截断面和底面的实形（这两个四边形都是分解成两个三角形，即各加一条对角线b01d01和bd0来画出的），即得截断后立体下半部分的展开图。

[例6-13] 如图6-16所示，设斜棱柱被通过点G且垂直于侧棱的P面所截，求截交线的投影、截断面实形和展开图。

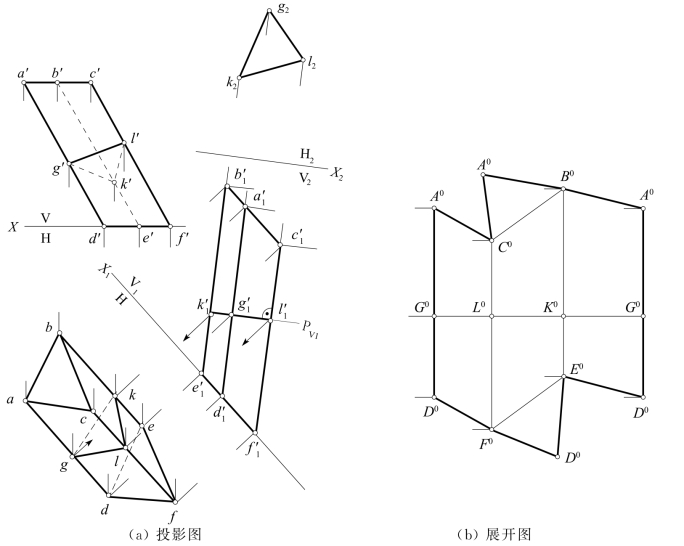
图6-16　斜三棱柱的截断

[解] 与棱柱的侧棱垂直的截平面、所形成的截交线和截断面，相应地称为法截面、法截线和法断面。

（1）投影图：由于各侧棱为一般位置直线，因而其法截面也是一般位置平面。为了能利用法截面P的积聚投影来求解法截线，应采用一个垂直于P面的辅助投影面如V1面。显然V1面必平行于棱柱的各侧棱，故X1∥ad等。在三棱柱的V1面投影中，过作垂直于侧棱的V1面投影等的直线PV1，即为P面的积聚投影。于是由PV1与和交得截交点的V1面投影，即可求出截交线的H面和V面投影△gkl和△g′k′l′。在H面投影中，因GK位于不可见棱面ABED上，故gk画成虚线；在V面投影中，因GK，KL分别位于两个不可见棱面上，故g′k′，k′l′也画成虚线。

设再作辅助投影面H2，使其平行△GKL，可得出反映法断面实形的H2面投影△g2k2l2。

（2）展开图：如图6-16（b）所示。

①作法一——先展开法截线：由于法截线的边线垂直于各侧棱。如LK垂直于CF和BE，因而在展开图中也互相垂直。又因V1面平行各侧棱，故，…等反映侧棱实长。

现于V1面投影附近，在PV1的延长线上，先作法截线的展开图G0G0，使G0K0=g2k2，K0L0=k2l2，L0G0=l2g2。再过G0，K0，L0，G0作G0G0的垂线，相应地与通过，…且平行于G0G0的各直线相交，即可得出各侧棱的展开图A0D0，B0E0和C0F0，于是可连得侧面的展开图。

最后，把反映顶面和底面实形的H面投影中两个三角形画入展开图中，即可作出完整的展开图。

为了作出斜柱面的展开图，常作任意位置的法截面P来作图。

②作法二——直接画侧面的展开图：如本图中，在V1面投影一侧作出A0D0，即作，且作即得A0D0。然后再以A0为圆心，长度AC（=ac）为半径作圆弧，即可与过且垂直于的直线交得C0。于是由C0作A0D0的平行线，再与通过所作的垂直于的直线交得F0。同法，可作出全部侧面的展开图，再延长PV1交得法截线的展开图，并加上顶面和底面的实形而完成整个展开图。