画法几何（第6版）：平面与立体点线

平面立体表面上点和直线的问题，可归结为平面上点和直线以及直线上点的问题。

1.平面立体上点和直线的可见性

凡是可见的棱面上点和直线，以及可见棱线上的点，都是可见的，否则是不可见的。

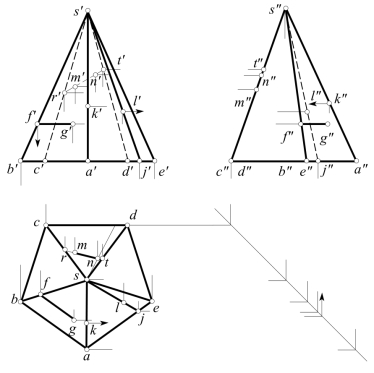
图6-6　五棱锥表面上点和直线

如图6-6所示的五棱锥表面上，点F位于棱线SB上，在朝向三个投影面观看时，SB都是可见的，故F是可见的。直线MN位于△SCD上。朝向H面观看时，△SCD是可见的，故MN也是可见而mn画成实线；但朝向V面观看时，△SCD是不可见的，故MN也是不可见而m′n′画成虚线。

2.由已知投影求作未知投影

已知棱面上点和直线的一个投影，以及棱线上一点的一个投影，可以求出其他投影，但若仅知它们位于棱面和棱线的积聚投影上的投影，则不能求出其余投影。(www.xing528.com)

（1）棱线上点——如图6-6所示，在五棱锥表面上，已知一点F的一投影f′，因f′在s′b′上，可知F在SB上，故由f′作连系线，可分别在sb和s″b″上定出f及f″。但若已知f和f″中的一个，如f，虽然f在ab上，但F可能在SB上，也可能在五边形的底面上，故有两解。如已指定在SB上，则可由连系线来定出f′及f″。

如已知SA上一点K的投影k，则要先求出k″后，再由之定出k′；当然，在两面投影中，也可用分比法或作辅助线来直接求出k′。

（2）棱面上直线——如已知△SAE上有辅助线SJ的一个投影sj，则定出j′、j″后，即可连得s′j′及s″j″。因在W面投影中，△SAE为不可见的，故SJ也不可见，故s″j″画成虚线。

又如已知△SAB上直线FG的一投影f′g′，因f′g′为水平线，可知FG为棱面上的H面平行线，必平行于棱面上的水平边AB，故在定出f后，由f作平行ab的直线，与通过g′的连系线来交成fg；由之再求出f″g″，同样是一条水平线。

又已知△SCD上直线MN的一投影m′n′。如无W面投影，则可把m′n′延长，与s′c′和s′d′交于点r′和点t′，即为MN延长后与SC、SD交点R、T的V面投影。按棱线上点的作法，先定出r和t，则连线rt即可与通过m′、n′的连系线，交得mn；至于m″n″，应位于△SCD的积聚投影s″c″（s″d″）上。所以也可由m′、n′作水平向连系线，求出m″、n″，再由m′、n′和m″、n″作连系线来作出mn。此外，仅知m″n″，则不能作出mn和m′n′。

（3）棱面内点——如已知△SAB和△SAE上点G和点L的一投影g′和l，则可分别过G和L点，作辅助线如H面平行线GF和过顶点S的连线SL，由它们与SB的交点F和与AE的交点J来定出各辅助线的H面和V面投影，从而作出g、g″和l′、l″。