画法几何：绕投影面旋转

1.点绕投影面垂直轴的旋转

一点绕投影面垂直轴旋转时：

（1）该点在旋转轴垂直的投影面上的投影，将在一个圆周上转动；

（2）该点的另外投影，将在与旋转轴的投影垂直的直线上移动，即平行于相应的投影轴方向移动。

图5-19（a）所示为空间一点A绕V面垂直轴O旋转时的状况，O的V面投影积聚成一点o′，旋转中心OA的V面投影与o′重合。旋转圆周的V面投影为通过a′的一个等大的圆周。半径为旋转半径的投影。旋转圆周的H面投影为通过a的一段直线，垂直于O的H面投影o，长度等于旋转直径，垂足oA为旋转中心OA的H面投影。

图5-19（b）为投影图。作图时，先作出旋转轴所垂直的投影面上的投影，由之再作出其他投影面上的投影。

当点A旋转至A1位置时，投影a′也沿同一方向旋转相同角度φ，至

图5-20为一点绕H面垂直轴O旋转至A1时的投影图。

以后规定，标记几何元素旋转后的位置时，根据旋转次数，于原来的字母右下方加注数字1，2等表示。投影图中，旋转轴和旋转中心一般不必注字。

2.直线和平面绕投影面垂直轴旋转

直线和平面等几何图形旋转时，几何图形上各点均沿相同方向旋转相同角度，故旋转后几何图形本身的形状和相互间位置不变。

直线和平面绕投影面垂直轴旋转，可有六种基本情况：

情况一——一般位置直线旋转成投影面平行线，旋转后的投影反映实长和对轴线垂直的投影面的倾角。

如图5-21（a）所示，有一条一般位置直线AB，以通过点B的一条H面垂直线O为轴，旋转至平行V面的位置A1B。则必等于直线AB的实长，且反映了与H面的倾角α。此时a1b必平行X轴且长度a1b=ab。

在投影图5-21（b）中，如已知ab、a′b′，欲求实长及倾角α，则先过任一点如B，取一条H面垂直线O为轴，o与b重合，o′为竖直方向；再使ab旋转成水平位置a1b，长度不变；最后由a1作连系线，与a′所作的水平线交得连线即反映AB的实长，且反映倾角α。

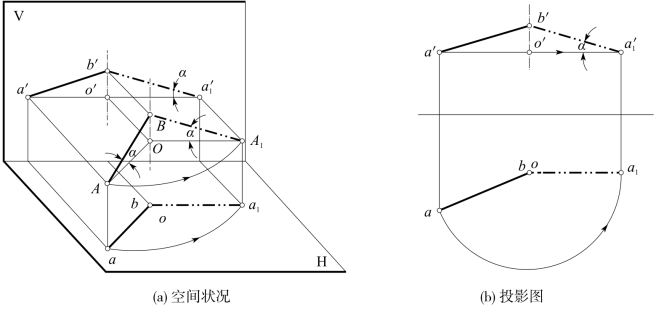
图5-21　一般位置直线旋转成投影面平行线

从本例可知，欲求一般位置直线的实长，可以把它旋转成任一投影面的平行线；欲求一般位置直线对某一投影面的倾角，则旋转轴应垂直于该投影面，而把直线旋转成另一投影面的平行线。在旋转轴所垂直的投影面上，直线旋转前后的投影长度不变。

为了在投影图上区别原来的投影与旋转后的投影，现规定旋转后的投影直线改用粗双点画线表示。

情况二——投影面平行线旋转成投影面垂直线，使旋转后的投影积聚成一点。

如图5-22（a）所示，AB为V面平行线，以通过点A的一条V面垂直线O为旋转轴，将AB旋转到垂直于H面的位置如B1A，则b1a必成一点，且与a重合则垂直于X轴。

在投影图5-22（b）中，如已知ab、a′b′，过点A取一条V面垂直线O为轴，o通过a并垂直于X轴，故o′与a′重合，使a′b′旋转成竖直位置，且，b1则与a重合。

从本例可知：某投影面平行线旋转一次，可旋转成另一投影面的垂直线，旋转轴应垂直于直线所平行的投影面。

情况三——一般位置直线旋转成投影面垂直线，使旋转后投影积聚成一点。

如图5-23（a）所示，一般位置直线AB，绕通过一点如B的垂直于一个投影面的轴旋转，如绕了H面垂直线O1旋转，因AB与H面的倾角不变，无法一次旋转成H面或V面垂直线，只能先如情况一那样，旋转成V面平行线A1B；再绕一条V面垂直线O2作第二次旋转，如情况二那样，才能旋转成H面垂直线。于是本情况实际上是情况一、情况二的合成。

图5-23（b）所示为投影图，实为图5-21（b）和图5-22（b）的连续作图。

从本例可知，欲将一般位置直线旋转成某投影面垂直线，应旋转两次，第一次旋转轴应垂直于该投影面，第二次旋转轴则垂直于另一投影面。

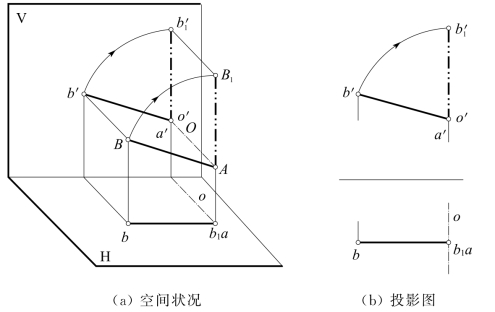
图5-22　投影面平行线旋转成投影面垂直线(www.xing528.com)

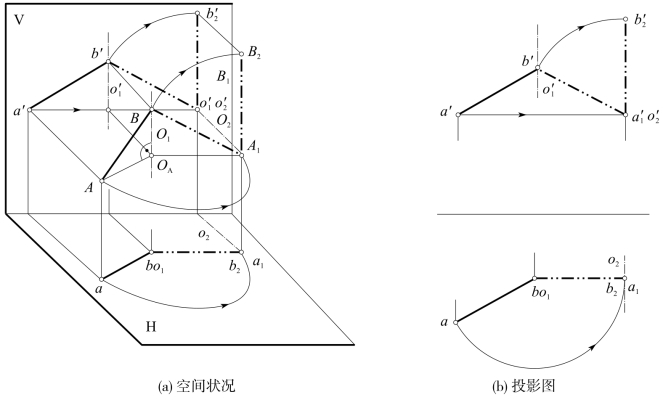
图5-23　一般位置直线旋转成投影面垂直线

情况四——一般位置平面旋转成投影面垂直面，使旋转后投影积聚成一直线并反映与旋转轴线所垂直的投影面的倾角。

在图5-24（a）中，如要把一般位置平面△ABC旋转成垂直于H面，可使三角形上某直线，如V面平行线BD，（如情况二）绕垂直于V面的旋转轴O，旋转成H面垂直线BD1，则△ABC必旋转成垂直H面的△A1BC1。

图5-24（b）为投影图。如已知△abc及△a′b′c′。在△ABC上取一条V面平行线BD即bd应水平，作出b′d′；并过点B取垂直V面的旋转轴O（o，o′）；再把b′d′绕o′（即b′）旋转成竖直方向，由之作出，于是a1bc1必成一直线。

旋转时，因△ABC对V面的倾角不变，故a1bc1能反映倾角β。

从本例可知：要将一般位置平面旋转成某投影面的垂直面，旋转轴应垂直于另一投影面，并先要在平面上取另一投影面的平行线。如要求出一般位置平面对某投影面的倾角，则应把平面旋转成另一投影面的垂直面。在旋转轴所垂直的投影面上，平面图形旋转前后的投影形状和大小不变。

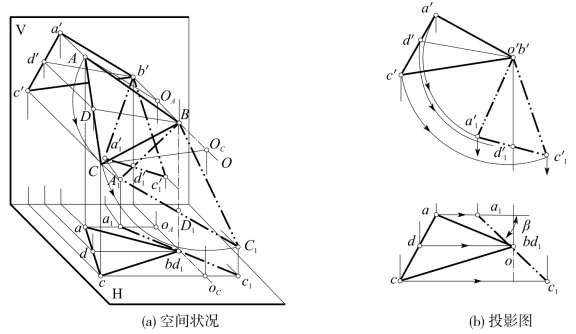
图5-24　一般位置平面旋转成投影面垂直面

情况五——投影面垂直面旋转成投影面平行面，使旋转后的投影反映平面的实形。

如图5-25（a）所示，△ABC为H面垂直面，以一条通过点C的H面垂直线O为轴，将平面旋转成平行V面的△A1B1C。此时，△A1B1C在H面上的积聚投影a1b1c必成水平方向；旋转后的V面投影反映△ABC的实形。

图5-25　投影面垂直面旋转成投影面平行面

图5-25（b）为投影图，作图线及结果如图所示。

从本例可知：某投影面垂直面旋转一次，能成为另一投影面的平行面，旋转轴则应垂直于平面所垂直的投影面。

情况六——一般位置平面旋转成投影面平行面，使旋转后的投影反映实形。

一般位置平面绕投影面垂直轴旋转时，只能旋转成另一投影面的垂直面；又平面与轴线所垂直的投影面间倾角不变，故不能旋转成任一投影面的平行面。而要先按情况四旋转成投影面垂直面，再按情况五旋转成投影面平行面。

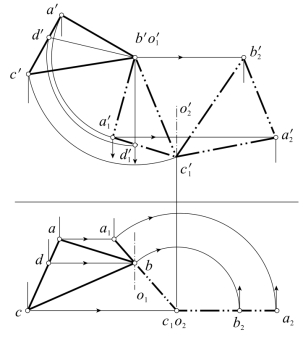
图5-26　一般位置平面旋转成投影面平行面

图5-26为投影图。设已知△abc及△a′b′c′。先过点B取V面垂直轴O1，按图5-24（b）所示，作出旋转后投影a1bc1及；再过点C1取H面垂直轴O2，按图5-25（b），作出旋转后投影a2b2c1及，于是反映了△ABC实形。

从本例可知：要将一般位置平面旋转成某投影面平行面，应旋转两次。第一次的旋转轴应垂直于该投影面，第二次旋转轴则垂直于另一投影面。

[例5-6] 求交叉两直线AB和EF间最短距离，如图5-27所示。

[解] 当交叉两直线的某同名投影互相平行时，它们间的距离就反映出所求的最短距离，参考表4-3。

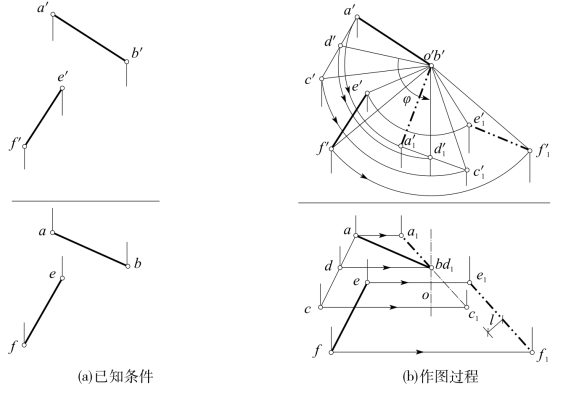
图5-27　求直线AB和EF的最短距离

如图5-27（b）所示，设过直线如AB上点A作任意长度直线AC平行EF，组成△ABC，则EF与△ABC互相平行。

EF随同△ABC绕通过点B的V面垂直轴O旋转时，EF始终平行△ABC的AC边。当△ABC上V面平行线BD旋转了角度φ，成为H面垂直线时，△ABC成为与H面垂直的△A1BC1。此时，a1bc1积聚成一直线。同时EF上各点也同方向旋转相同的角度φ至E1F1位置。e1f1∥a1bc1，它们间的距离l就是所求的最短距离。