点、直线和平面作图题解法

根据前面介绍的一些作图题，总结如下：

1.综合作图题的内容

（1）对象综合——包含有点、直线和平面等几何元素；

（2）条件综合——包含已知条件、要求条件、解题性和作图方法等的综合。

2.解题顺序

（1）空间分析；

（2）确定解题方法；

（3）投影作图；

（4）总结答案结果。

3.解题方法

根据题意文字和图形中已知条件和要求条件，选择一种或综合的合适方法。

（1）综合分析：如图4-38中求点与平面间距离的作图步骤；

（2）利用轨迹方法；(www.xing528.com)

（3）分析已知条件和要求条件间的关系，如图4-39（a）中分析情况；

（4）辅助作图法：如图3-5（b）中分析直线实长、倾角、投影长度和坐标差等关系的图形；

（5）由分析要求对象或想象中的要求结果来得到的解题方法；

（6）变更内容的间接方法，如图4-41、图4-43利用余角、补角方法；

（7）利用第五章的投影变换法等。

[例4-19] 过已知点A作直线AF，平行于已知△BCD，且与已知直线E相交于F点。已知条件如图4-46（a）所示。

[解] 因AF平行于△BCD而位于通过点A且平行于△BCD的轨迹平面上；又AF与E相交而位于点A与直线E所构成的轨迹平面上，故AF为这两个轨迹平面的交线。由于此交线上一点为A，另一点实为直线E与平行△BCD的轨迹平面的交点F。

现如图4-46（b）所示，过点A作AK∥BC，AL∥BD，则AK、AL所确定的平面，即为过点A而平行于△BCD的轨迹平面。

再求出E与该轨迹平面的交点F，求法如图所示，则连线AF（af，a′f′）即为所求。

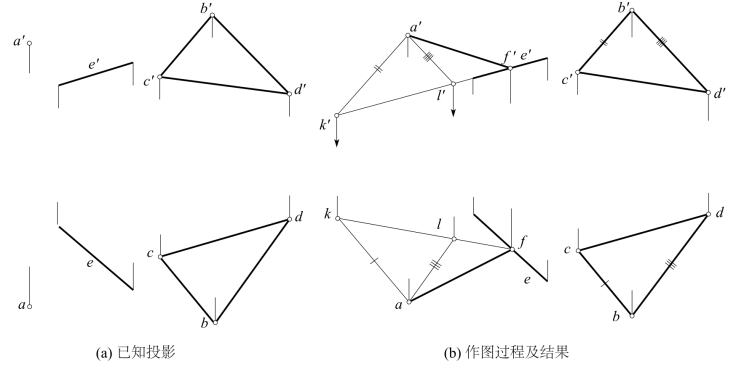
图4-46　过点A作直线AF平行△BCD，且与直线E相交