解决位置情况下的角度问题

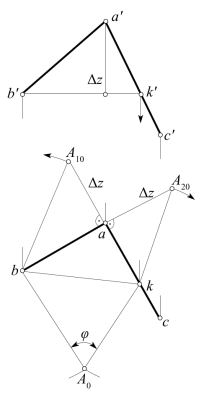
图4-40　相交两直线间夹角

1.两直线间的夹角——求相交的两条一般位置直线间夹角，可任作一直线与角的两条边线相交，组成一个三角形。求出该三角形的实形，即可得出夹角的实大。

如求交叉的两条一般位置直线间夹角，可过任一直线上任一点，作一直线与另一直线平行，就成为求该相交两直线间夹角的问题。

[例4-15] 求相交两直线AB和AC间夹角φ的实大，如图4-40所示。

[解] 作一直线BK与AC相交于点K。为了作图方便，可作一条投影面平行线，如H面平行线BK，则bk反映其实长。再求出AB和AK的实长（bA10，kA20），即可作出反映△ABK实形的△bA0k，则∠bA0k=φ。

2.直线与平面间的夹角

（1）直接求法：过已知直线作一平面垂直于已知平面，求出两平面的交线，则交线与已知直线间的夹角，即为已知直线和平面间的夹角。空间状况如图4-41所示，求直线AB与平面P的夹角φ，可过AB上任一点A，向P面引垂线AK，AK和AB与P面的交点K和B间连线KB为通过AB且垂直于P面的平面与P面的交线。于是AB与BK间的夹角φ，即为AB与P面间的夹角。

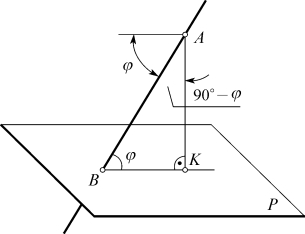
图4-41　直线AB与平面P间夹角φ的空间示意图

（2）求余角的间接方法：如图4-41所示，AK与AB间的夹角BAK为φ的余角，即等于90°-φ，由其求出余角即为φ。

[例4-16] 求直线AB与△CDE间夹角φ的实大，如图4-42所示。

[解] 设用间接法解：为了由AB上任一点A，作直线AK⊥△CDE，故在△CDE上作H面平行线CF和V面平行线CG，于是可作出AK的方向。(www.xing528.com)

再作一条H面平行线BK，利用前法，求出△BAK的实形△bA0k，则∠bA0k=90°-φ，由此可定出余角φ。

3.两平面间的夹角

（1）直接方法：作一个辅助平面垂直于已知两平面，交于两条交线，交线间的夹角即为两平面间的夹角。如图4-43所示，求平面P和Q间的夹角φ，作辅助平面垂直于平面P和Q，交线为BL和KL。它们之间夹角有两个，互为补角。除成直角外，一个为锐角，一个为钝角。两平面间夹角，以锐角为准。但此法较繁，通常用间接的方法。

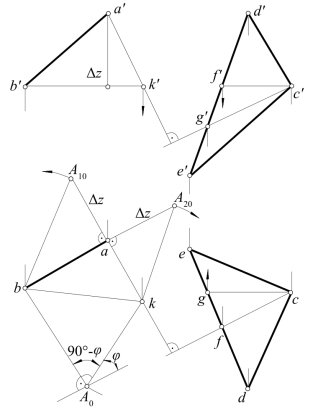
图4-42　AB与△CDE的夹角φ

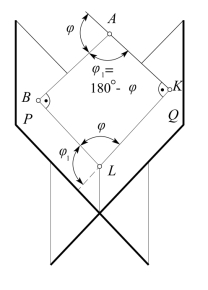
图4-43　两平面P、Q间夹角φ的空间示意图

（2）求补角的间接方法；空间状况如图4-43所示。可在空间任取一点A，分别向P和Q引垂线AB和AK。若它们之间的夹角为锐角，即表示两平面间夹角φ；本图中垂线间的夹角φ1为钝角，则其补角φ才表示两平面间夹角大小，故本图中AB和AK夹角实为φ1的补角，即180°-φ1。

[例4-17] 求△CDE与△RST间夹角φ的大小，如图4-44所示。

[解] 任取一点A，分别向两个三角形引垂线AK和AB，都是利用垂直于两个三角形上投影面平行线作出的。

再取一条H面平行线BK，与AB和AK相交于点B、点K，求出表示△ABK实形的△A0bk，因∠bA0k＜90°，即表示两平面间夹角φ的大小。如大于90°，则其补角才为两平面间夹角。