画法几何中,根据几何形体的一些已知投影,要求在满足某些几何条件的情况下,利用几何原理和投影特性,作出几何形体本身或另外几何形体的投影;或者解决几何形体本身的或相互间的形状、大小、方向和距离等问题,都称为图解问题。为了区别起见,前者称为定位问题。后者称为量度问题。例如:已知两平面的投影,求作交线的投影,是定位问题;求夹角的实大,是量度问题。包含有量度的定位问题,如求作一平面平行一已知平面且成某一已知距离,仍作为量度问题。
关于点、直线和平面的图解问题,不少以前已经叙述过,现再总述如下。
1.定位问题,可分为以下几种:
(1)从属问题——①直线上点;②平面上点和直线。
(2)相联问题——①过两点作一直线;②过不在同一条直线上三点、一直线和线外一点、两相交直线、两平行直线作一平面。
(3)相交问题——①两直线的交点;②直线与平面的交点;③两平面的交线;④三平面的交点。
2.量度问题,可分为以下几种:
(1)直线和平面本身的量度问题——①直线段的实长;②平面图形的实形。
(2)距离问题——①两点间距离;②一点与一直线间距离;③两平行直线间距离;④两交叉直线间距离;⑤点与平面间距离;⑥平行的直线与平面间距离;⑦两平行平面间距离。
(3)角度问题——①两直线间的夹角(相交或交叉);②一直线与平面间的夹角(包括直线对投影面的倾角);③两平面间的夹角(包括平面对投影面的倾角)。
(4)平行问题——①两直线互相平行;②直线与平面互相平行;③两平面互相平行。(https://www.xing528.com)
(5)垂直问题——①两直线互相垂直(相交或交叉);②直线与平面互相垂直;③两平面互相垂直。
平行和垂直问题,可视为角度问题的特殊情况。当夹角为零时为平行;当夹角为90°时为垂直。平行也可视为相交的特殊情况,即将交点或交线视为位于直线或平面上无穷远处。
又如直线段的分比和角度的分角等问题,可归结为直线段的实长和平面图形的实形问题。
当点、直线和平面本身或相互间对投影面处于特殊位置时,常常能够由投影直接反映量度,或使定位和量度问题简化。除了前面各章节中已有叙述外,现将主要内容列于表4-3中。
表4-3 直接反映量度或便于定位的特殊情况
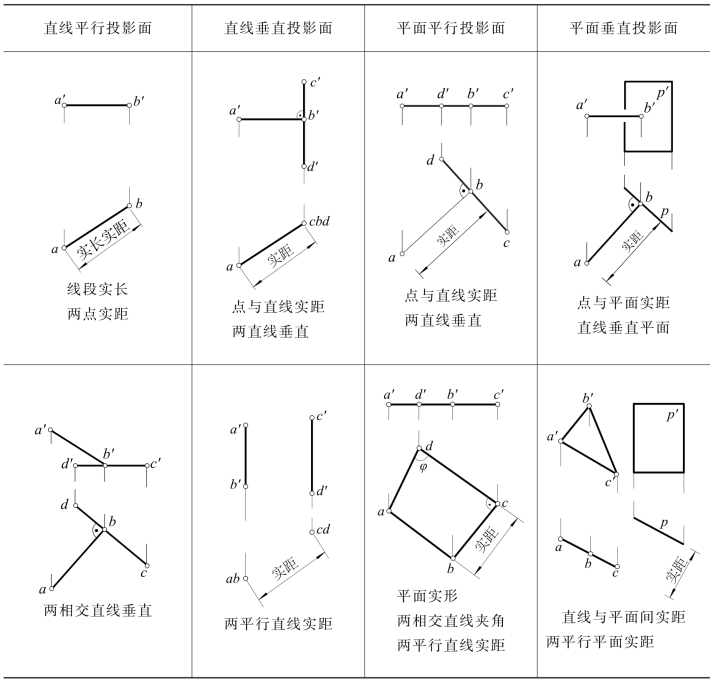
续表

当直线和平面处于一般位置时,除了前面章节已有叙述外,下面将有关距离、角度和作图题的解法,分别予以介绍。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




