1.用直线与平面的交点作图:求两个一般位置平面的交线,可先求出两个平面上任意两条边线对另一个平面的两个交点,然后连线取两平面的公共部分。这两条边线可属于同一个平面,也可分属于两个平面。
(1)解题前,先观察投影图上没有重影的平面图形边线,它们不可能与另一平面在边线范围内有交点。故不必求取这种边线对另一平面的交点。如图4-34中边线BC,AC,EF,DG。
(2)如图4-34所示,已知△ABC与四边形DEFG的两面投影,求交线MN的投影。可根据图4-33的方法,先求出四边形中两条边线如DE和FG与△ABC的交点M和N,再连得交线MN,作法如图所示。
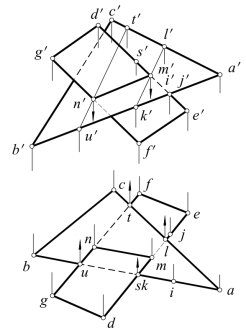
图4-34 两平面的交线MN(全交)
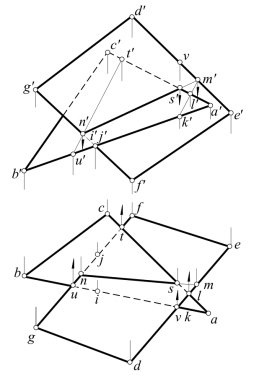
图4-35 两平面的交线NS(半交)
在投影图中,不重影部分的边线,说明在空间没有被遮住而画成实线。至于重影部分的可见性,可按直线与一般位置平面相交的可见性来判别,交线为可见与不可见的分界线。由重影点判别可见性,如图4-34所示。
(3)图4-35也为求△ABC与四边形DEFG的交线。但此图中,投影d′e′与△a′b′c′的交点m′已越出△a′b′c′的范围,点M实际上是DE与△ABC平面扩大后的交点。连线MN与AC交于点S,可知实际的交线仅为线段NS。(https://www.xing528.com)
图4-34 中两平面的相交,称为全交,即一个平面完全穿过另一个平面;图4-35中两个平面则称为半交,即两个平面只交到一部分。
2.直接用辅助平面作图:求两个一般位置平面的交线,也可取具有积聚性投影的平面,一般取两个投影面的平行面为辅助平面,分别求出它们与两个已知平面的辅助交线,每个辅助平面上两条辅助交线的交点,是所求交线上的点。两个辅助平面共求得两点,它们的连线,即为所求交线。
如直观图4-36(a)所示,两已知平面分别由平行两直线A,B和相交两直线C,D所确定,它们的交线为E。
作一个H面平行面P为辅助平面,与已知两平面的辅助交线为FG和IJ。它们的交点为K。
同样地再作一个Q面,得到另一个交点L。则连线KL即为两已知平面的交线。
图4-36 (b)为投影图,作图过程如图所示。
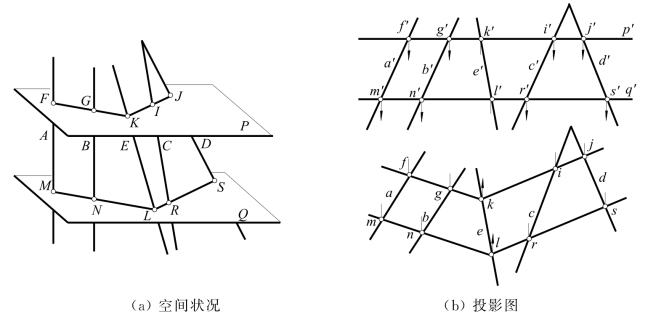
图4-36 辅助平面法求两平面交线
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




