1.一般位置平面的各个投影，不会积聚成直线，也不能反映平面的实形和明显地显示对投影面的倾斜情况，只是与空间的平面形状成类似的图形。
平面对投影面的倾斜情况，由它们之间的夹角来表示。平面与投影面的夹角，称为平面的倾角。平面对H面、V面和W面的倾角，分别用希腊字母α，β和γ来表示。
2.平面对某一投影面的倾角，可由该平面上垂直于任意一条同名投影面平行线的任一条最大斜度线的倾角来表示。
在图4-9（a）所示的轴测图上，P平面上有一条AM直线垂直于H面迹线PH，求证在P平面上只有这种方向的直线对H面的倾角为最大。
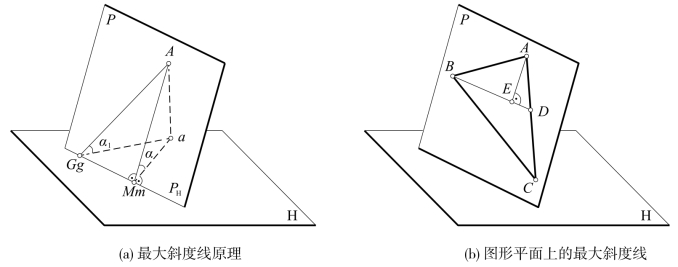
图4-9 平面上的最大斜度线
设AM与H面的倾角为α，也即为AM与其H面投影am的夹角。
因为AM⊥PH，而PH是H面上的直线，故二者的H面投影也应相互垂直，即am⊥PH。在P平面上另取任意方向的直线，例如：由点A连接PH上任意点G，得直线AG，并设它与H面的倾角为α1，即AG与其H面投影ag的夹角。只须证明∠α＞∠α1，则P平面上只有AM方向的直线对H面的倾角为最大。
因为α=arctan
，但在直角三角形amg中，ag是斜边，故ag＞am，因此α＞α1。这种AM方向的直线便称为P平面上对于H面的最大斜度线。
在投影图中，通常是不画出迹线的；由于在平面上的投影面平行线就是其同面迹线的平行线，因此，平面上对于投影面的最大斜度线，也就是垂直于同面的投影面平行线的直线。如图4-9（b）所示，要作出△ABC平面上对H面的最大斜度线，只要先过三角形上的任一点（例如：顶点B），在三角形平面上作H面平行线BD；再在三角形平面上又任取一点（例如：另一顶点A），通过它作上述H面平行线BD的垂直线AE，即为△ABC平面对H面的最大斜度线。
3.求平面对某投影面的倾角，可按以下三个步骤进行。
（1）先在平面上任作一条该投影面的平行线；
（2）再在该面上任作一条最大斜度线，垂直于所作的投影面平行线；(www.xing528.com)
（3）此最大斜度线的倾角，即为平面的倾角。，而α1=arctan
[例4-4] 如图4-10所示，已知△ABC的投影，求倾角α和β。
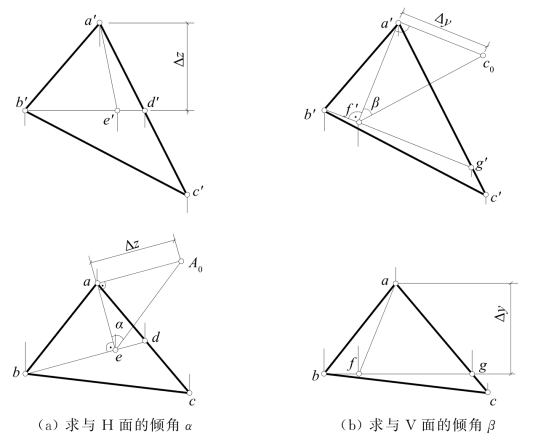
图4-10 求△ABC的倾角α和β
[解] 如图4-10（a）所示，先在平面上任作一条H面平行线BD，其b′d′应为水平，再任作一最大斜度线如AE⊥BD，则ae⊥bd；最后，求出直线AE的倾角，如图中的∠A0ea为△ABC的倾角α。实际上，投影a′e′线不必作出。
又如图4-10（b）所示，在平面上作V面平行线如BG，则bg应水平；然后作最大斜度线AF⊥BG，则a′f′⊥b′g′；再求出AF的倾角β，如图中的∠C0f′a′即为△ABC的倾角β。
[例4-5] 如图4-11所示，已知屋面▱ABCD及其上水滴E的两投影，求水滴E沿屋面滚落时的轨迹以及屋面与H面的倾角α。
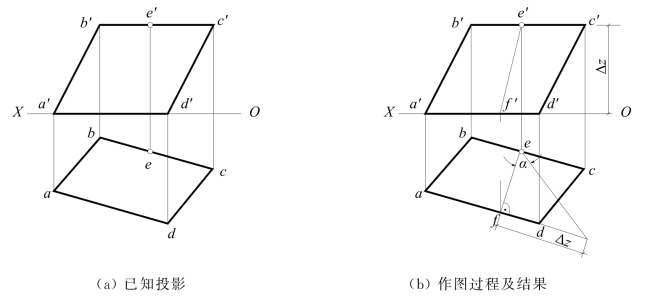
图4-11 求水滴从屋面滚落时的轨迹及倾角α
[解]
（1）因屋面为一平行四边形，其BC及AD边均为水平线，从e向bc或ad所引的垂线ef，必为屋面上对H面的最大斜度线的H面投影，从而得到e′f′。
（2）屋面上的水滴必沿着对H面的最大斜度线滚落，而EF就是最大斜度线，故EF就是水滴滚落时的轨迹。如图4-11（b）所示，利用直角三角形法，可求出EF与H面之间的倾角α，即为屋面与H面的倾角。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
