1.直角的两边平行于某投影面时,则在该投影面上的投影仍是直角。
因当夹角的两边平行于某投影面时,由于每边的投影与每边本身平行,故两边的投影间夹角,反映了两边本身之间夹角。故当夹角为直角时,投影也成直角。
2.当直角的两边之一平行某投影面,另一边不平行也不垂直于该投影面,则在该投影面上的投影也呈直角。
如图3-20(a)所示,相交两直线AB和BC,设AB⊥BC,且AB平行H面,BC为一般位置直线。因Bb垂直H面,故AB⊥Bb,于是AB垂直于投射平面BbcC;又因AB平行H面,即ab∥AB,所以ab也垂直投射平面BbcC,因而ab垂直于投射平面BbcC上直线bc,即ab⊥bc。故此时直角的投影还是直角。图3-20(b)是投影图。
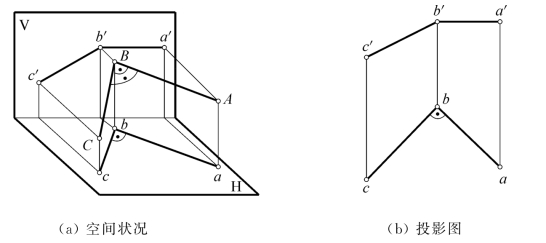
图3-20 一边平行于投影面的直角的投影
3.反之,相交两直线之一是某投影面平行线,且两直线在该投影面上的投影互相垂直,则在空间两直线也互相垂直。
在图3-20(b)中,直线AB和BC的H面投影ab⊥bc;又因a′b′水平,可知AB为H面平行线。于是在图3-20(a)中,因直线AB平行H面,故AB∥ab;又因ab⊥bc,则ab垂直于投射平面BbcC,故AB也垂直此投射平面,因而AB垂直此平面上直线BC。
4.当空间交叉垂直的两直线之一平行于某投影面,另一直线不平行也不垂直于该投影面时,则这两直线在该投影面上的投影也垂直;反之也是。(https://www.xing528.com)
如图3-21(a),设直线AB与DE交叉垂直,且AB为H面平行线,DE为一般位置直线。现过AB上任一点如B,作直线BC∥DE,则AB⊥BC,且ab⊥bc。因BC∥DE,则bc∥de,故ab⊥de。反之也是。图3-21(b)为投影图。
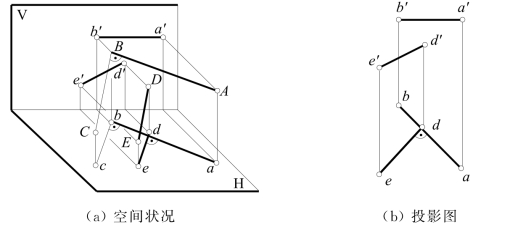
图3-21 一直线平行投影面的交叉垂直两直线的投影
[例3-10] 如图3-22所示,求点A到V面平行线CD的真实距离。
[解] 可过点A作直线CD的垂线,设垂足为B,则AB的长度即为所求距离。
因CD平行V面,故AB和CD的V面投影垂直。作图时,可由a′作a′b′⊥c′d′,垂足为b′;由此求出b,可连得ab。再利用直角三角形法,作出反映AB真实长度的线段aB0,其长度即为点A到CD的真实距离。
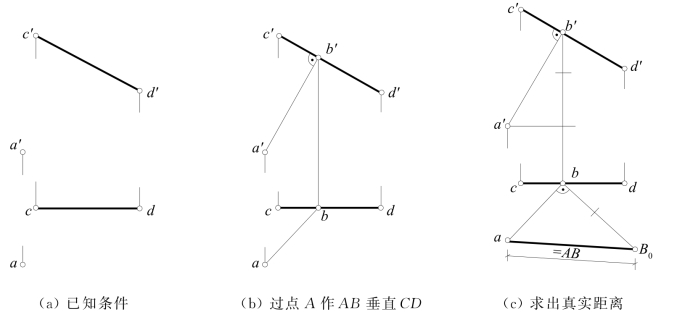
图3-22 求点A到直线CD的距离
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




