直线位置与实长倾角的求解方法

1.一般位置直线的各投影均呈倾斜方向，没有积聚性，也不反映直线的真实长度和倾角，如图3-4所示。

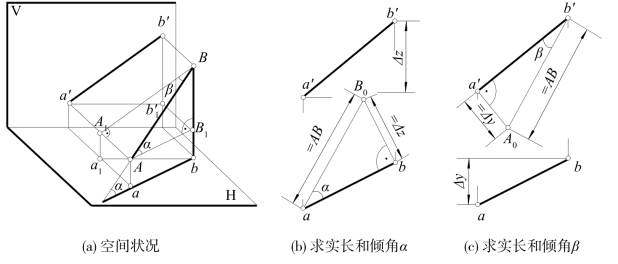
图3-4　线段AB的实长及倾角α和β

直线与投影面所成的夹角，称为直线的倾角。直线对H面、V面和W面的倾角，分别用小写希腊字母α，β，γ表示。

直线对某投影面的倾角，由直线与它在该投影面上投影之间的夹角来确定。在图3-4（a）中，直线AB与ab间夹角α，即为AB对H面的倾角。它不能由一般位置直线的投影直接反映出来。

2.直角三角形法。由直线的投影求一般位置直线的实长和倾角。

如图3-4（a）所示，设在通过AB且垂直于H面的投射平面AabB内，由点A作一水平线AB1∥ab，与Bb交于一点B1。因Bb⊥ab，故在△ABB1中，BB1⊥AB1，因而△ABB1是一个直角三角形。AB为该直角三角形的斜边；∠BAB1=a；底边AB1=ab；另一直角边BB1=Bb-B1b=Bb-Aa，即A和B两点离开H面的高度差Δz，可由a′和b′两点的高度差Δz表示出来。

于是在投影图中，如图3-4（b）所示，作一直角三角形，以ab为底边，另一直角边bB0=a′b′的高度差Δz。则斜边aB0反映线段AB的实长，∠baB0=α。

又如在图3-4（a）中，通过AB且在垂直V面的投射平面内，由点B作BA1∥b′a′，则△ABA1中，∠ABA1=β。故可在投影图中，如图3-4（c）所示，作一直角三角形a′b′A0，可求出AB的实长和倾角β。

反映直线实长和倾角的三角形如△abB0、△a′b′A0，可作于投影ab，a′b′的任一侧，也可作于投影的任一端。

这种利用一个直角三角形求直线实长和倾角的方法，称为直角三角形法。

该直角三角形的一直角边等于该直线的一个投影；另一直角边等于该直线的两个端点到该投影所在投影面的距离差；斜边的长度等于直线的实长；而斜边与该投影之间的夹角，等于直线对该投影所在投影面的倾角。

由此可知：利用一个投影面上的直角三角形，反映出该投影面上的投影（长度）、直线上两个端点到该投影面的距离差、直线本身的实长和直线对该投影面的倾角等四个要素之间的相互关系，因而已知任意两个要素都可通过作出直角三角形来求得其余两个要素。(www.xing528.com)

如作出直线的W面投影，同样可以求出倾角γ。

3.已知直线的实长、倾角等作投影图。根据上述的直角三角形法，已知直线的实长、倾角等，可作出投影图。

[例3-1] 设直线AB长27mm，倾角α=45°，β=30°，已知前方左下端点A的投影a，a′如图3-5（a）所示，作全直线AB的两面投影，如图3-5（c）所示。

图3-5　已知AB和a，a′及实长、倾角，作全投影图

[解] 已知实长和倾角，故在图3-5（b）处，作出反映实长和倾角的两直角三角形。于是得出投影的长度ab，a′b′和坐标差Δy，Δz。因而在图3-5（c）中，在点A的后方右上角，可作出点B的投影b和b′，即可连得直线AB的投影ab和a′b′。

[例3-2] 在直线AB上取一点C，使点C离V面、H面的距离之比为3∶2。

图3-6　作直线AB上点C和点D的投影

[解] （1）点距H面的距离为它的Z坐标，点距V面的距离为它的Y坐标。能同时反映出Z坐标和Y坐标的是W面投影，故此题可由W面着手，先求出点C的W面投影c″，再求c′及c。

（2）因Y∶Z=3∶2，在OYW轴上取3个单位，在OZ轴上取2个单位可得点l″，连Ol″，则Ol″上所有的点其Y和Z坐标之比均为3∶2，故Ol″与a″b″之交点即为c″，再根据c″可求得c′及c。