数列极限计算常与函数极限计算、方程实根个数计算、定积分大小比较、积分和式极限计算以及与数列极限定义有关的函数求导、积分运算等结合成综合题.
例02.5 设数列{xn}的递推式为x1∈(0,π),xn+1=sinxn(n=1,2,…),求数列极限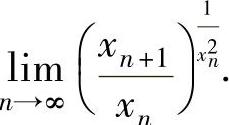
精解 先计算极限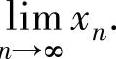
由{xn}的定义可知0<xn+1=sinxn<xn (n=1,2,…),
所以{xn}单调减少且有下界,因此由数列极限存在准则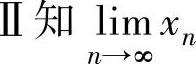 存在,记为A,则A∈[0,
存在,记为A,则A∈[0,
1).
对递推式两边令n→∞取极限得A=sinA.
显然,在[0,1)上,上述方程仅有解A=0.所以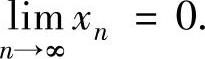
由于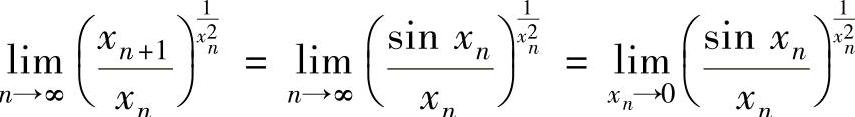 ,
,
所以考虑函数极限
其中
将它代入式(1)得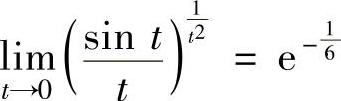 ,
,
因此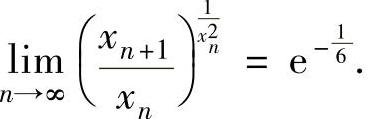
例02.6 设函数fn(x)=ex+x2n+1.
(1)证明:对任意正整数n,方程fn(x)=0都有唯一实根.
(2)记上述唯一的实根为xn(n=1,2,…),求极限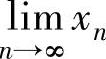 的值A,并证明:xn-A~
的值A,并证明:xn-A~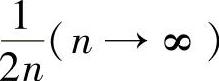 .
.
精解 (1)对n=1,2,…,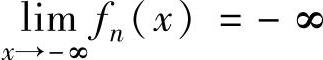 ,
,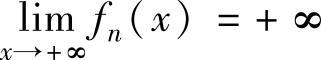 ,所以由连续函数零点定
,所以由连续函数零点定
理(推广形式)知方程fn(x)=0有实根.此外,由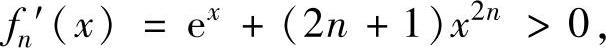
即fn(x)是单调增加函数,所以对n=1,2,…,方程fn(x)=0的实根都是唯一的.
(2)容易观察到fn(-1)=e-1-1<0,fn(1)=e+1>0,所以方程fn(x)=0的唯一实根xn∈(-1,1)(n=1,2,…).
由fn(xn)=0,即exn+x2nn+1=0得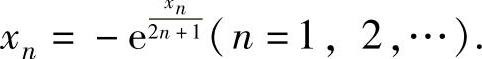
上式两边令n→∞取极限得
于是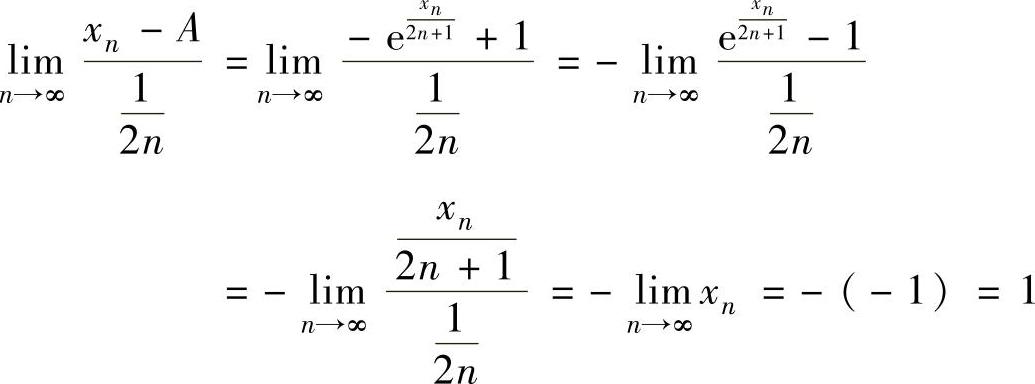 ,(https://www.xing528.com)
,(https://www.xing528.com)
即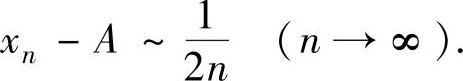
例02.7 求下列和式极限:
精解 (1)记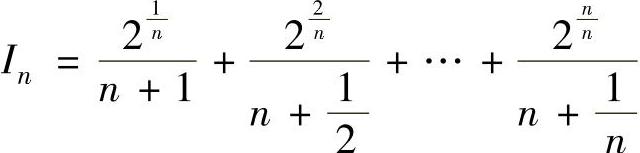 ,它不是某个函数的积分和式,现对它作
,它不是某个函数的积分和式,现对它作
适当的缩小与放大得
且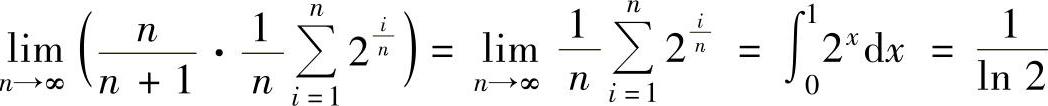 ,所以由数列极限存在准则Ⅰ得
,所以由数列极限存在准则Ⅰ得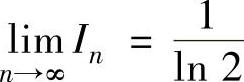 ,即
,即
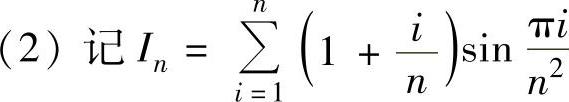 ,它不是某个函数的积分和式,现对它作适当的缩小与放
,它不是某个函数的积分和式,现对它作适当的缩小与放
大.
显然,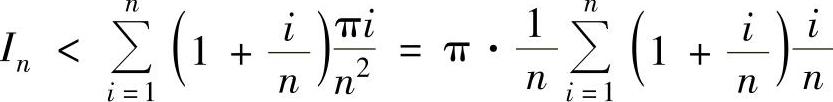 ,
,
此外,利用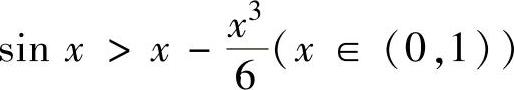 (证明见本题注)可得
(证明见本题注)可得
所以,对n=1,2,…,有
且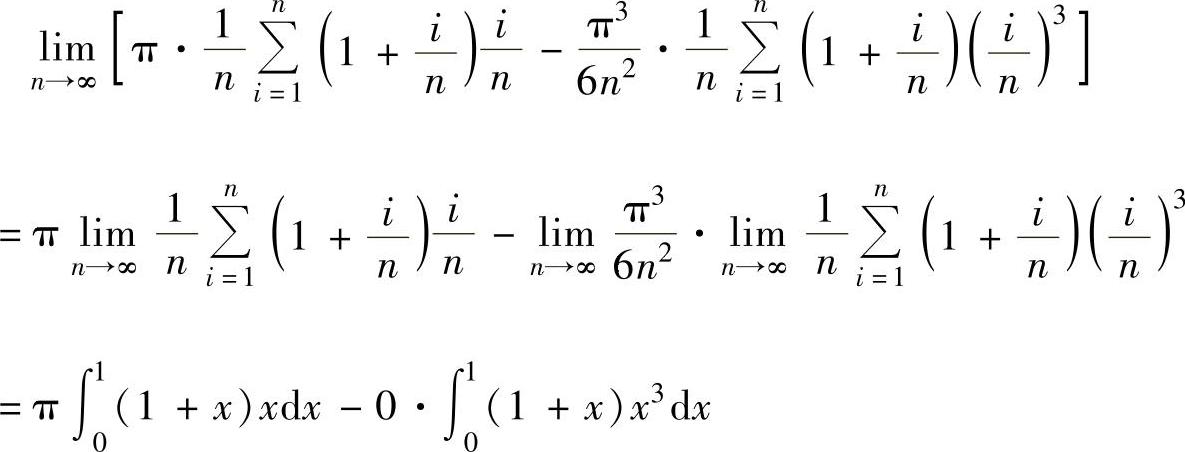
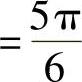 ,
,
因此由数列极限存在准则Ⅰ得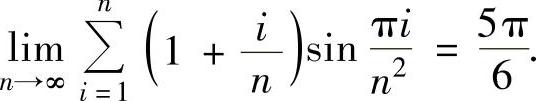
注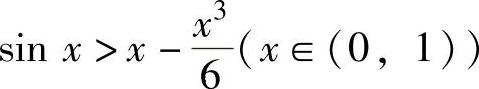 的证明如下.
的证明如下.
令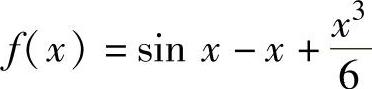 ,则
,则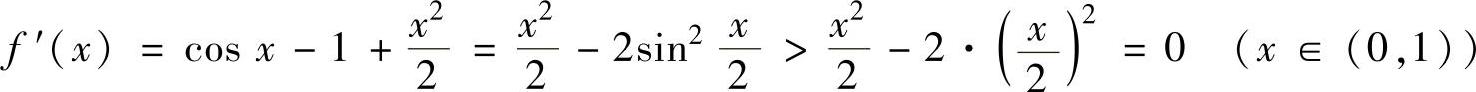 ,
,
所以,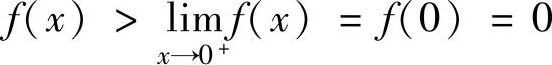 ,即
,即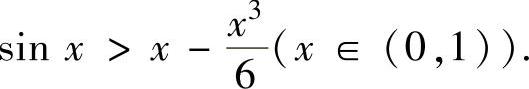
例02.8 设函数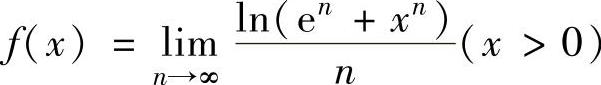 ,求函数
,求函数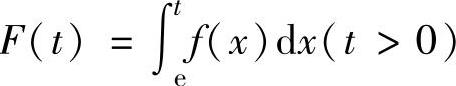 的表
的表
达式.
精解 先算出f(x)的表达式,为此需按x与e的大小关系分0<x≤e与x>e两种情形考虑.
当0<x≤e时,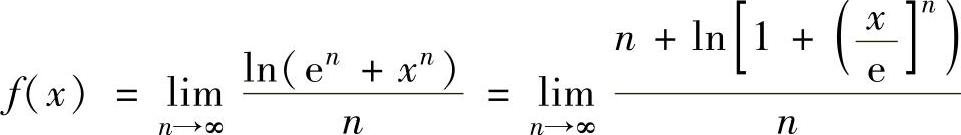
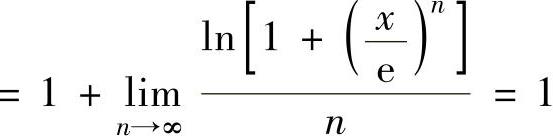 ,
,
当x>e时,f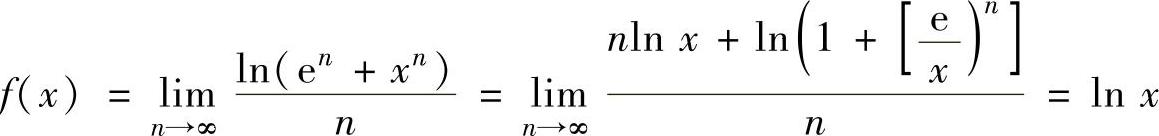 ,
,
所以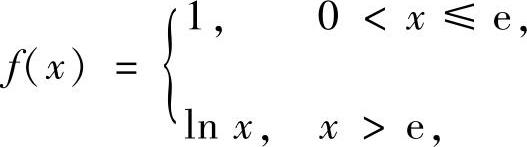 因此
因此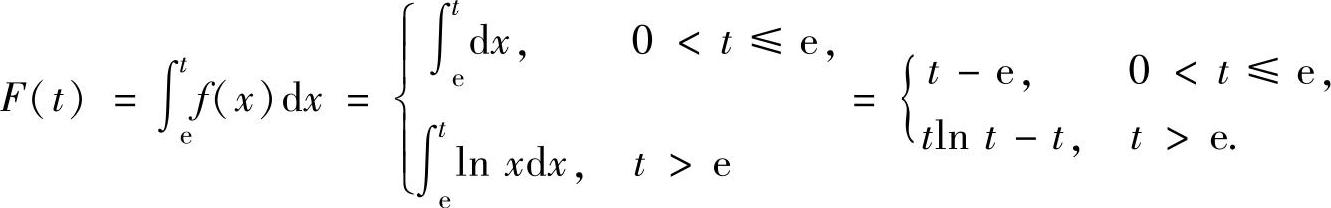
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




