这里的数列极限是指那些不易用数列极限运算法则或转换成函数极限计算的数列极限.解决这类数列极限计算问题的快捷方法是应用数列极限存在准则Ⅰ或准则Ⅱ.
准则Ⅰ:设有数列{xn},{yn}和{zn},如果yn≤xn≤zn (n≥N,N是某个正整数),
且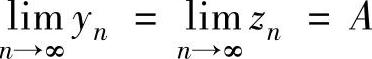 ,则
,则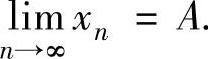
准则Ⅱ:设数列{xn}单调不减有上界或单调不增有下界,则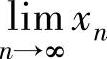 存在.
存在.
注 (ⅰ)应用准则Ⅰ快捷地算出数列{xn}的极限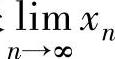 的关键是快速地找到准则Ⅰ
的关键是快速地找到准则Ⅰ
中要求的数列{yn},{zn},它们可以通过对xn作适当缩小与放大得到,其中下列不等式是常用
的.
(ⅱ)当数列{xn}由递推式x0,xn+1=f(xn)(n=0,1,2,…)确定时,总是先用准则
Ⅱ确定数列{xn}的极限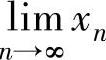 存在,记为A,然后对递推式xn+1=f(xn)的两边令n→∞取极
存在,记为A,然后对递推式xn+1=f(xn)的两边令n→∞取极
限得A=f(A).解此方程算出A的值.
在使用准则Ⅱ确定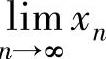 存在时,首先要判定数列{xn}的单调性与有界性,后者是比较
存在时,首先要判定数列{xn}的单调性与有界性,后者是比较
容易判定的,而前者有以下三种判定方法.
方法1:如果xn+1-xn≥0(n≥N,N是某个正整数),则{xn}单调不减;如果xn+1-xn≤0
(n≥N,N是某个正整数),则{xn}单调不增.
方法2:如果{xn}是正项数列,则当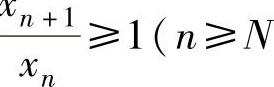 ,N是某个正整数)时,{xn}单调不
,N是某个正整数)时,{xn}单调不
减;当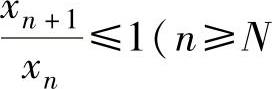 ,N是某个正整数)时,{xn}单调不增.
,N是某个正整数)时,{xn}单调不增.
方法3:将递推式中的f(xn)改写为f(x).如果f(x)单调增加(例如f′(x)>0),则{xn}单调,并且当x1<x2(x1≤x2)时,{xn}单调增加(单调不减);当x1>x2(x1≥x2)时,{xn}单调减少(单调不增).
例02.1 计算下列极限:
(1)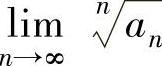 ,其中
,其中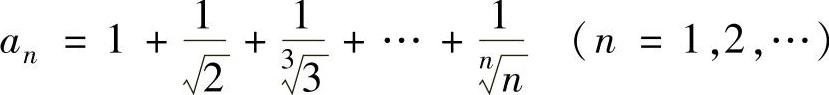 ;
;
(2)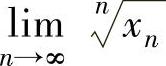 ,其中
,其中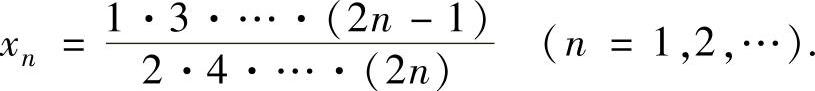
精解 用数列极限存在准则Ⅰ计算所给的两个数列极限.
(1)由1≤an≤n得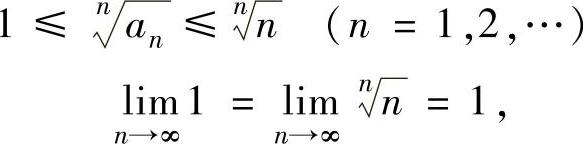 ,且
,且
所以,由数列极限存在准则Ⅰ知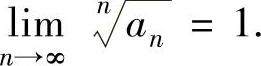
(2)显然,
为了对xn作适当放大,引入数列
由于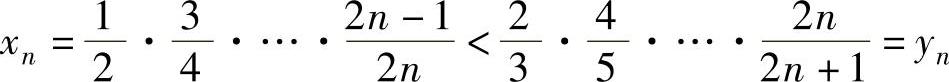 ,所以有
,所以有
即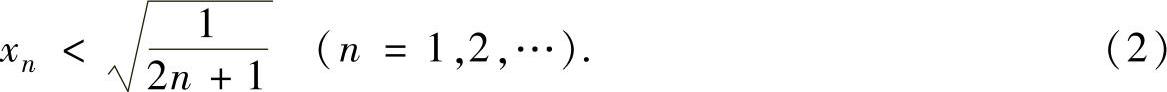
由式(1)、式(2)得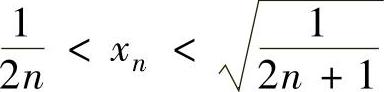 ,即
,即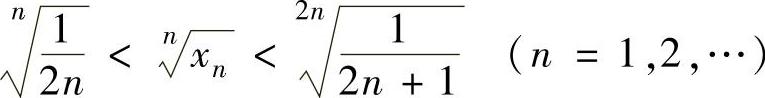 ,
,
并且 ,所以由数列极限存在准则Ⅰ得
,所以由数列极限存在准则Ⅰ得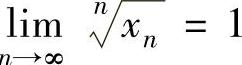 .
.
例02.2 设数列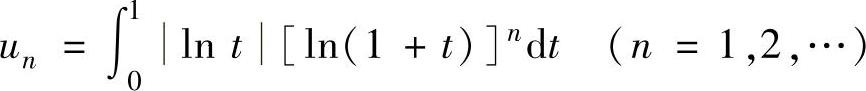 ,求极限lim
,求极限lim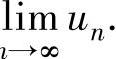
精解 显然un>0(n=1,2,…).另外,由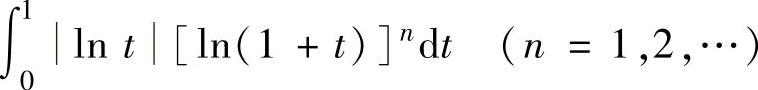 和
和 都是收敛的反常积分,以及对n=1,2,…,有
都是收敛的反常积分,以及对n=1,2,…,有
lnt[ln(1+t)]n<(ln2)nlnt (t∈(0,1))
知,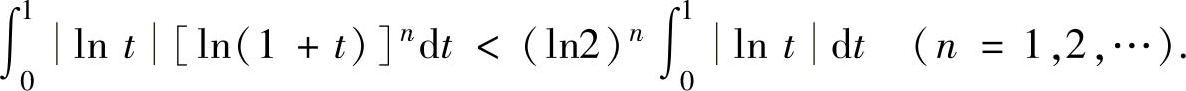 (https://www.xing528.com)
(https://www.xing528.com)
于是对n=1,2,…有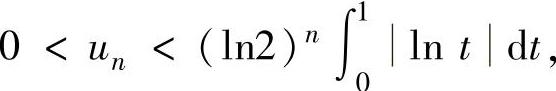
且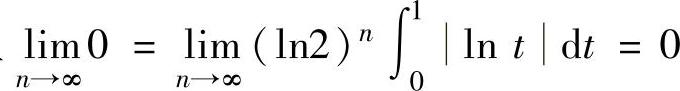 ,所以由数列极限存在准则Ⅰ得lim
,所以由数列极限存在准则Ⅰ得lim
n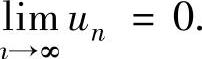
例02.3 计算下列极限:
(1)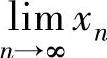 ,其中数列{xn}是由递推式
,其中数列{xn}是由递推式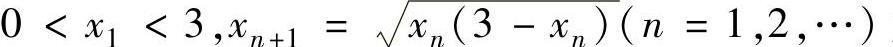 定
定
义的;
(2)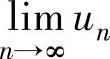 ,其中数列{un}是由递推式u1=1,
,其中数列{un}是由递推式u1=1,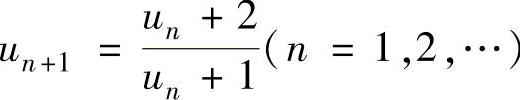 定义的.
定义的.
精解 由于问题(1)和问题(2)的数列都是由递推式定义的,所以宜用数列极限存在准
则Ⅱ计算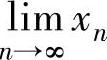 和
和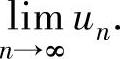
(1)由数列{xn}的定义知数列{xn}是正项数列,于是对n=1,2,…有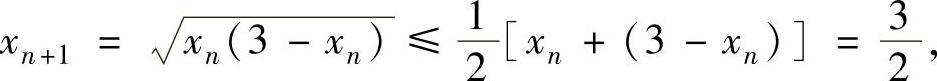
即数列{xn}有上界.
将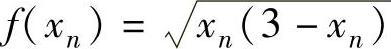 中的xn改为x得函数
中的xn改为x得函数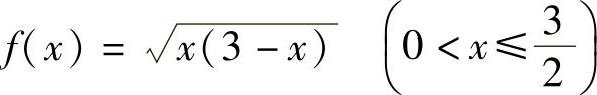 .由于
.由于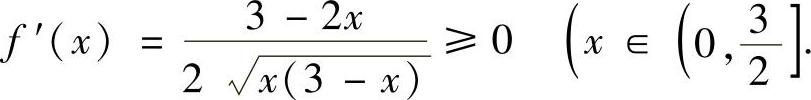 仅在点
仅在点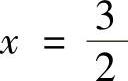 处取等号),
处取等号),
且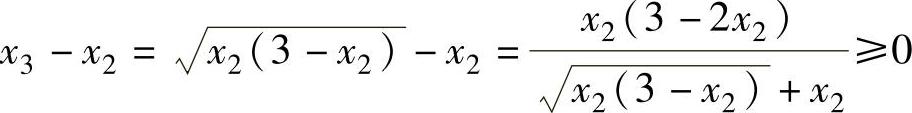 ,所以{xn}也是单调不减数列.
,所以{xn}也是单调不减数列.
于是由数列极限存在准则Ⅱ知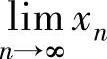 存在,记为A,则A
存在,记为A,则A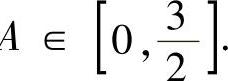
对所给的递推式两边令n→∞取极限得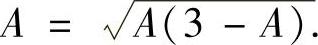
解此方程得A=0,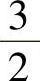 .由于A≥x2>0,所以A=0不合题意,因此A
.由于A≥x2>0,所以A=0不合题意,因此A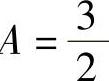 ,即
,即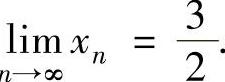
(2)将f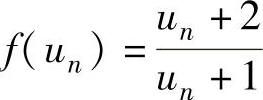 中的un改为u得f
中的un改为u得f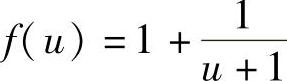 .由于
.由于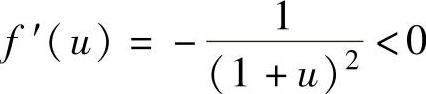 ,即
,即
{un}不是单调数列,因此将{un}划分成两个子数列{u2n-1}和{u2n}.
由于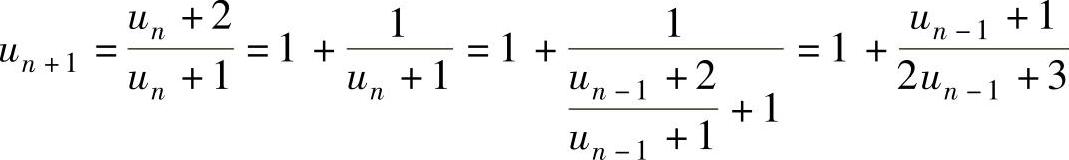 ,所以{u2n+1}有递推式:
,所以{u2n+1}有递推式:
u1=1,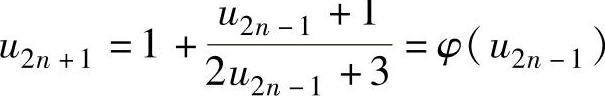 (n=1,2,…).
(n=1,2,…).
将上式中的u2n-1改为u得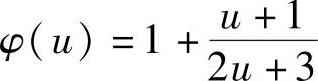 ,则
,则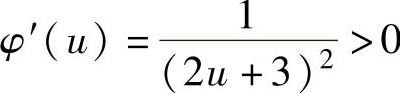 ,即{u2n+1}是单
,即{u2n+1}是单
调数列.此外,由{u2n+1}的递推式可知,{u2n+1}是正项数列,且由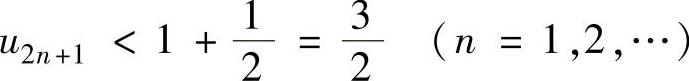
知{u2n+1}既有上界又有下界.因此由数列极限存在准则Ⅱ得到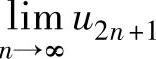 存在,记为A,则
存在,记为A,则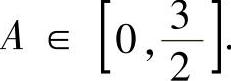 在{u2n+1}的递推式
在{u2n+1}的递推式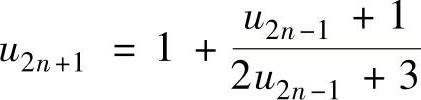
的两边令n→∞取极限得A ,解此方程得
,解此方程得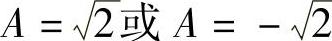 (不合题意,舍去),
(不合题意,舍去),
所以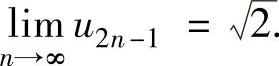 同理可得lim
同理可得lim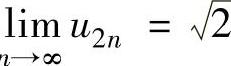 .因此
.因此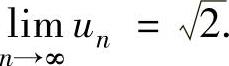
例02.4 设数列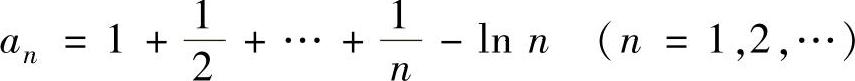 ,证明:
,证明: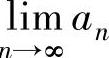 存在.
存在.
精解 数列{an}虽不是由递推式定义,但仍可以由数列极限存在准则Ⅱ来证明,即只要证明{an}单调减少且有下界即可.为此引入不等式
(该式可通过对f(x)=ln(1+x)在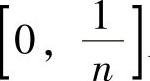 上应用拉格朗日中值定理得到证明),于是对n=
上应用拉格朗日中值定理得到证明),于是对n=
1,2,…有
即{an}单调减少.此外,由
知{an}有下界.
因此由数列极限存在准则Ⅱ知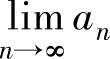 存在.
存在.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




