网络安全和保密的重要性

如果计算机都集中在计算中心，由于任何数据未经许可拿不出计算中心，非法人员也难以进入计算中心，所以保证安全是容易的。但网络的出现使情况发生了根本的变化，已经无法利用人力去管理每天传送于网络内计算机之间的无数信息。为了使这些信息不在传输路径上或其它什么地方被人窃取，需要采取某种保密方法。这种方法被称为加密（Encipherment）。

加密的一般过程是：

①发送方将报文进行加密处理，即将明文变换为密文；

②密文通过通信网传送，在此过程中，密文有可能被窃听，或因干扰者注入干扰报文而被篡改；

③接收方将接收到的密文进行解密处理，即将密文变换成原来的明文。

在此过程中，通信双方的通信内容即使被窃取，但只要窃取者不知道通信过程所采用的加密与解密方法或找不到适当的破译方法，通信就是安全的。从上述过程可见，数据流进入表示层，已变换过的数据流再从该层中流出，即完成了加密/解密的过程。这种变换就是表示服务的一种。

实际上，从物理层到应用层间的每一层都能进行加密。如图7.1.1（a）所示，在信息进入线路前先经过一个硬件加密装置，信息到达另一端时再经一个硬件解密装置，就可使在通信线路上传送的信息是加了密的。这种方法被称为数据链路加密，只要更换硬件加密/解密装置，就可以变换加密方法，而不需改变已有的软件。另一种方法是端—端加密。如图7.1.1（b）所示，这种方法既可以利用软件也可以利用硬件，由表示层来实现。两种方法各有所长，用途也不一样。

密码技术包括密码设计技术（即密码表示方法）及密码破译技术（即密码分析方法）两个方面。

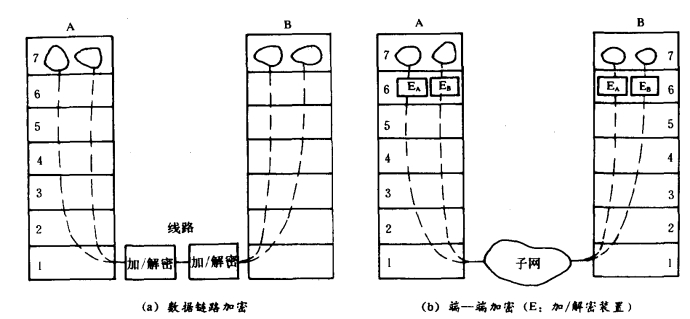
图7.1.1　两种网络加密方法

加密过程可表示为

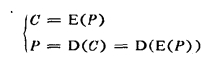
即明文（plain text）P经以密钥K为参数的函数E变换后输出密文C，C又在接收方经以同样的密钥K为参数的函数D，变换为P.

在传统的密码技术中，常常采用一些较为简单的方法，例如，将字母移位进行替换：

明文a 　b 　c 　d 　e f 　g 　h 　i 　j 　k 　l 　m 　n 　o p 　q...

密文D E F G H I J K L M N O P 　Q R S T...

这种替换法就是上述函数E，密钥为移位值K=3，解密则是上述替换的反变换。还有另外一些传统的方法，如相乘法、易位法等。这些方法共同的特点是必须对E、K、D进行严格的保密。加密模型如图7.1.2所示。

图7.1.2　加密模型（双密钥密码系统）

传统密码学进入现代密码学的两大标志是1977年美国国家标准局颁布的数据加密标准DES，及Diffle和Hellman于1976年发表的划时代论文《密码术的新方向》，文中提出了一种全新的密码系统的概念。与传统的密码系统不同，在这种系统中，加密变换E与解密变换D是不对称的，两者没有简单的互导关系，但须满足以下要求：

①D（E（ P ））=P ；

②不可能通过计算从E推导出D；

③不可能通过计算直接破译E。

满足了这三项要求，即使将加密算法E或其加密钥K公开也无关紧要，故这种方法被称为公开密钥法（public key）。

当计算机网络采用公开密钥法进行保密通信时，所有网络用户（如A、B、C等）都公布各自的加密算法（EA、EB、EC等），且通常将它们记载到可读的文件中。当A与B通信时，A方将其明文P按B方的EB加密成EB（P）后发往B，B收到后再按其解密算法将EB（P）解密，即DB（EB（P））=P；而若C收到了EB（P），由于其不知道DB，故无法破译EB（P）.当B与A通信时，B方用A方的EA来加密明文，A方自再DA进行解密。

为了便于具体地了解公开密钥法，下面介绍两种著名的密码算法。

1、MIT算法（指数密码）

该密码算法以数论为理论基础，具体步骤如下：

①选取素数p，q，并使它们都大于10100；

②计算 n=p×q和Φ（n）=（p-1）（q-1）；

③选取一个与Φ（n）互素的数a；

④求出满足方程a×b modΦ（n）=1的b；那么对明文P＜n（用数字表示），加密变换和解密变换分别为：

E=Pbmodn，b为密钥；

D=Ca mod n，a为密钥。其中b可以公布，a则需保密。

显然，如果破译者能分解n的因子，就能找到p和q，从而算出Φ（n）和a，所以该算法的安全性是建立在大数n的因子分解十分困难这一基点上的。尽管数学家已经努力研究了300多年，但大数因子分解问题仍然没有多大的进展，现在已知最快的分解算法需要的运算次数为T=exp（sqrt（ln（n）ln（ln（n））））.假设一次运算需1ms，当n＞10200时，这需要200万年以上的计算时间。

［例］ 将明文apple用MIT法进行加密和解密。

［解］ 首先选择两个素数p=3，q=11（为简便起见不用p、q＞10100的规定），则

n=p×q=3×11=33(www.xing528.com)

Φ（n） =（p-1）（q-1）=2 × 10=20

再选一个与Φ（n）互素的数a=7（因7与20无公因子），则由

7×bmod 20=1

可得　b=3

故　　E=P3（mod 33）

D=C7（mod 33）

将字母用两位十进制数表示，如“a”=01，“b”=02，“c”=03，…，“z”=26，则P满足0≤P≤33.

明文apple的数字表示为0116161205，按MIT算法形成密文C和解密成明文P的过程如表7.1.1所示。

表7.1.1

故apple的密文为数字表示0104041226，字母表示为addlz.当选取素数很大时，可以很好地加密。

2、背包密码算法

所谓背包密码算法是指背包里放有n种物体中的某些种，已知n种物体每种的重量和背包的总重量，要求出背包中究竟装有哪些物体的算法。当n很大时，这是十分困难的。背包问题的数学描述是：给定一个由正整数构成的向量A=（a1，a2，…，an）（各种物体的重量）和一个正整数C，求一个二进制向量M=（m1，m2，…，mn）其中mi=0或1，使得

C=AM

或

求解n个元素的任何背包问题的最好已知算法需O（2n/2）数量级的时间和O（2n/4）数量级的空间。

但是存在一类简单背包问题，它满足条件：

求解简单背包问题很容易，其算法如下：

Algorithm Sknap（B，A）∶｛“简单背包问题的解”｝

FOR i∶=n TO 1 DO

BEGIN

IF C＞=a［i］THEN m［i］：=1 ELSE m［i］∶=0；

C ∶=C-a［i］*m［i］

END；

IF C=0 THEN sknap∶=M ELSE｛“无解”｝

1978年，斯坦福大学的Markle和Hellman给出了把简单背包问题转化为带窍门的复杂背包问题的具体方法。其步骤如下：

①选取一个很容易用方程C'=A'M求解的简单背包向量

A'=（a1'a2'… an'）

②选取整数u，使

③选取与u互素的整数w，求出满足方程w-1×w mod u=1的w-1；

④计算a=w×ai'mod u，从而把简单背包向量转化为带窍门的复杂背包向量

A=wA'mod u

这时求解C=AM很困难，但在知道窍门信息w-1和u，并设C'=w-1C modu时，就可以把它转化为简单背包问题

C'=w-1C mod u=w-1AM mod u=w-1（wA'）M mod u=A'M

把带窍门的复杂背包问题用于双密钥密码系统中，公开密钥即为复杂背包向量A，保密密钥是窍门信息u和w-1.