计算机网络原理：高效分析协议效率

所谓协议效率即协议的信道利用率。影响协议效率的因素是多种多样的。为了将原始的传送机构转变为无差错的信道，从而实现有效、正确的传输，协议需要增加许多额外的传输开销，例如增加帧同步字符、校验字段、应答信息等。这些都直接增加了传输一定位纯数据的开销，即需要消耗一定的辅助字符传送时间来完成传送协议。另外，协议本身的特性也将影响协议的效率，如报文帧是固定长还是可变长，采不采用搭载应答（即随反向信息帧进行应答），采用连续发送的管道方式还是停等方式，采用半双工传输线路还是全双工传输线路，以及传输线路的错误统计特性等等。除了极端理想的情况外，所有的协议效率都不会达到100%.

为便于推导协议效率，首先作如下一些约定：

A=应答帧的比特数；

C=以bps为单位的信道容量或数据速率；

D=每帧中的数据位数；

F=D+H（即帧全长），假设帧长是一定数（时间为t帧）；

H=每帧中的报头长

I=中断及CCP服务时间 +传播时间（tprop）；

L=一个帧或其应答丢失或受损的概率；

P1=一个数据帧丢失或受损的概率；

P2=应答帧丢失或受损的概率；

R=每数据帧平均重发次数；

T=定时器时限长度；

U=协议效率或信道利用率；

N=窗口尺寸。

在很多情况下，协议效率的推导是十分复杂的，需要许多数学方面的知识，如排队论、概率统计、图论等方面的知识。为了避免陷入复杂的数学推导之中，本书将仅介绍几个典型的协议效率的推导过程。

简单的协议效率为

U=传送数据所用时间/实际所花费的时间(www.xing528.com)

讨论效率时，常常选取协议过程的一个典型周期。对图4.1.2所示的例子，tprop=t1-t0=t5-t4=t7-t6=t11-t10=t13-t12为传播时间；tENQ=t2-t1，tACK=t4-t3=t10-t9，tData=t8-t7，tEOT=t14-t13分别为询问信号、应答、数据和结束信号的传送时间；tproc1=t3-t2，tproc2=t6-t5=t12-t11，tproc3=t9-t8为处理时间，所以，实际花费的总时间为

t总=tENQ+2tACK+tData+tEOT+tproc1+2tproc2+tproc3+5tprop=t14-t0

传送数据实占时间为tData，故协议效率为

U=tData/t总

这里所讨论的是一般的理想情况，若考虑线路出错的情况，还要根据平均的重发次数进行计算，即把重发所占用的时间也计算到总时间中去。

通常，一帧中的报头和数据是应区分的，这时计算U时，分子应仅为数据位，分母为总开销，即

U=D/（H+D+其它开销）

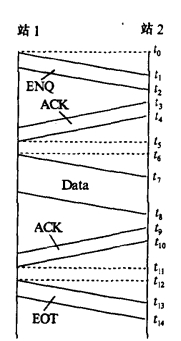
图4.1.2　一典型传输周期

式中其它开销为转化为位的时间。如果一帧中的报头及应答帧长相对于全帧可以忽略不计，则可将分子用整个帧长所占时间代替。例如，前例中，tData可能就是含有报头开销的帧的传送时间。

这里再定义一个特殊的参数

a=tprop/t帧

传播时间等于链路的距离d除以媒质的信号传播速度V，一般为3×108m/s，但在硬媒质上的典型值为2×108m/s，传输时间等于帧长L除以数据率C，所以

a=（d/V）/（L/C）=Cd/VL

这样，a与数据速率及链路的距离成正比，它是决定数据链路性能的一个最重要的参数。对a的一种有用的解释是，它代表用比特表示的媒质长度（Cd/V）与帧长之比，在分析协议效率时常会用到这个参数。

协议效率的另外一个说法为有效数据率。虽然每一链路都有一个传送速率，如1200bps、600bps等，但这是物理的和电气的性能。增加了数据链路控制后，因为在数据链路控制中要花费一些重传的时间和传输一些辅助的比特，信宿（收方）实际收到的信息速率将有所降低。所以，有效数据率常用来衡量一条链路的好坏及协议性能的高低（通信效率和吞吐量）。有效数据率实际即为协议效率与链路传送速率之积。