网络信道传输速度-计算机网络原理

计算机网络目前大都采用模拟信道，因此，收发计算机都需要安装调制解调设备，以完成数字信号和模拟信号之间的转换。在这种点—点式信道中，关于传输速度有两种概念，即信道速率和信道容量。

1、信道速率

常见的信道速率有调制速率和数据速率两种。调制速率是指调制器出口或解调器入口的信号速率。这种用来载荷信息的正弦波信号通常称为载波信号，因此调制速率实际上取决于载波信号的频率。调制器的作用是把信源输出的每一位数字（一个二进制位，或多个二进制位形成的数字）调制到载波上。设载波信号的周期为T秒，则调制速率B（上限）为

其单位为波特（baud）。数据速率是指信源入出口处每秒钟传送的二进制脉冲（码元）数。每一个二进制码元称为一个比特（bit）或位，所以数据速率的单位为比特/秒或位/秒，记作b/s或bps.

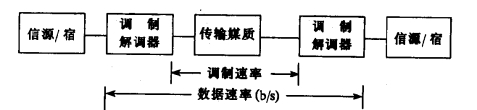
图3.1.4　信道速率

设每一个载波周期内可以载荷的信号状态数为n，则数据速率C与调制速率B之间的关系为

当调制解调器采用调幅制时，通常每一调制周期T发送一个比特（即n=2的情况），则C=B.例如，调制速率为1200波特的调制解调器可以选择载波频率为1200Hz，数据速率为1200b/s.为了提高数据速率，既可以提高载波信号的频率，也可以提高在载波信号的每一周期内发送的比特数。如采用调相制时，每一调制周期可以载荷2个比特或3个比特，即n=4（四相调制）或n=8（八相调制）的情况，这时C=2B或C=3B.部分数据速率C，调制速率B及信号状态数n之间的关系如表3.1.1所示。

表3.1.1

两种速率之间一般只使用数据速率C，而较少使用调制速率B，尤其是n=2时，二者数值相等，但仍然不要混淆二者的区别。利用表3.1.1，可以很快地得出二者的关系，如数据速率要达到9600b/s，可选用16相调制的调制解调器，且调制解调器本身的调制速率为2400波特。

2、信道容量

在计算机通信领域中，关于信道容量的相近术语很多，且时常混合使用，很容易使人产生混淆。常见的术语有带宽、最大数据速率及信道容量。无论采用何种术语，无非都是要说明某信道传送数据的最大能力，也即最快的传输速度。(www.xing528.com)

带宽（bandwidth）指的是一个信道所能传输的频率范围。如果一个信道的最低可传频率是f1，而最高可传频率为f2，则其带宽为

可见，带宽并不能说明传输速度有多高，它只是指明所覆盖的频率范围有多大。可以通过某种手段将某一频带移入更高的频带，但若带宽不变，则信道的传送能力不变。由于信道传输信息的能力与其带宽成正比，因此有时候用带宽这个术语来表述信道容量。

早在1924年，H.Nyquist就认识到这个基本限制的存在并推导出表达无噪声有限带宽信道最大数据速率的公式。Nyquist证明，若任意信号通过一个带宽为ω的低通滤波器，则此被滤波的信号靠每秒恰好2ω个采样即可重新构成，采样速率比每秒2ω快是无意义的，因为采样所要恢复的高频成份已被滤除。如果信号由n个离散电平表示，则Nyquist的采样定理可表示为

式中Cmax为最大数据速率。

［例］电话信道的带宽为3000Hz，传输300～3300Hz频带的信息。试求在电话信道上所能传送的二进制信号的最大数据速率。

［解］Cmax=2×3000×log22=6（kbps）

在有噪声的情况下，就要采用“信噪比”的概念。如果用S表示信号功率，N表示噪声功率，则信噪比为S/N.通常并不直接使用S/N，而是用101g（S/N）（计量单位为分贝，写成dB）。若S/N是1000，则分贝值为30分贝；若S/N是100，则分贝值为20分贝。Shannon导出了有噪声信道的信道最大数据速率为

对于上例电话信道，若信噪比为30dB（这是电话系统的典型参数），则不论信号电平数是多少，采样速度是高是低，信道的最大数据速率为

30000b/s是数据速率的理论极限值，实际上很难达到。Shannon的结论是利用信息论得出的，具有普遍的正确性，但它仅是一个上限；Nyquist的结论则要涉及电平数目，不管怎样，Nyquist公式所得出的值是不能超越Shannon公式所规定的上限的，否则就像永动机一样是不可能实现的。

一般情况下，Shannon公式给出的是最大信息传送速率，是与最大数据传送速率不等价的，正如数据和信息是不同的概念一样。但在计算机网中，常把二者都作为信道的容量来使用，二者的度量单位都是b/s.带宽与传送速率成正比，在概念不混淆的情况下，也可用来描述信道的传输速度。