三类方程解性质比较-数理方程典型应用案例分析

1）解的光滑性

在经典意义下，作为一个二阶偏微分方程的解，要求有方程中出现的那些二阶偏导数，并且要求它们连续。因而对经典解来说，它总是所考虑区域中相当光滑的函数。但是，对不同类型的方程来说，解的光滑程度却不相同。例如，对弦振动方程来说，从达朗贝尔公式可见，如初始条件u（0，x）＝φ（x），u1（0，x）＝φ（x）中的φ（x）∈C2，φ（x）∈C1，且φ（x）的三阶导数不存在，则解的三阶偏导数也不存在。对高维波动方程，利用泊松公式也可看到类似的事实。对于热传导方程来说，情况就不一样，从热传导方程解的表达式（见第1章式（1.44））可以验证，只要初始条件φ（x）是有界的，解u（x，t）在t＞0时就是无穷可微的；而当将t固定时，解还是空间变量的解析函数。对于拉普拉斯方程，其解的光滑性更好，它的任何连续解在解的定义区域内都是解析函数。

可以从三类方程所代表的物理现象来解释这些事实。拉普拉斯方程描写平衡与稳定的状态，表达这些状态的解应该是非常光滑的；热传导现象具有能迅速地趋于平衡的特点，因而解也比较光滑。而双曲型方程所描述的波的传播现象，却并不如此。在波的传播中，可以将一定的弱间断性保留下来（例如存在波阵面），因而解就可能不很光滑；在解的更广泛意义下，甚至还可以有带更强的间断性的解。

同时，如方程有非齐次项或者变系数的时候，解的光滑性质还要受到系数与非齐次项光滑性的影响。

2）解的极值性质

拉普拉斯方程与热传导方程都存在极值原理，但它们所采取的形式是有些区别的。对拉普拉斯方程而言，它的解反映已处于稳定状态的物理量，因而当解不是常数时，在内部不能取极值；同时，其边界的各个部分原则上没有什么本质上的区别，因而极值可能在边界上任一处达到。至于热传导方程，由于热量的传播速度很快，所以初始时如内部有极值，那么在t＞0时内部极值就迅速消失，因而区域内部的最大值不能超过区域初始时刻及侧面边界上的最大值。双曲型方程通常就没有这样的性质，这是因为波的传播可以互相叠加，扰动增大的现象往往会在叠加时出现。

3）影响区域与依赖区域

从影响区域和依赖区域来看，三类方程也有很大的区别。对波动方程而言，一点的影响区域为以该点为顶点向上做出的特征锥内部（在三维时为锥的表面），决定特征锥斜度的a就是波的传播速度；一点的依赖区域就是以该点为顶点向下做出的特征锥与平面t＝0所交的圆（或球面）。对热传导方程而言，一点的影响区域是该点以上的整个上半平面，因为只要经过一瞬时，在极远处就会受到该点扰动的影响，扰动传播的速度似乎是无限的；而一点的依赖区间就是整个直线t＝0。对于拉普拉斯方程，它是定常型的，因而没有传播速度，但可以考虑这样的问题：在边界曲面Γ的部分曲面Γ1上给出不等于零的边界值，而在其余部分Γ－Γ1上假定解为零，此时相应边值问题的解u（x，y，z）是否只是在区域Ω的一部分区域Ω1上取不等于零的值，而在其余部分Ω－Ω1上恒为零？如果这样，那么这部分区域Ω1就可以称为曲面Γ1的影响区域。回答是否定的，因为根据调和函数的解析性定理，如果u在一很小区域上恒等于零，则它必在整个区域上恒等于零，从而在Γ1上也只能取等于零的边界值。因此在曲面Γ上任意小的部分Γ1给出边界值，它的影响区域必是全部区域Ω。另外，由于解析性定理对于很广泛的一类椭圆型方程成立，因而这事实也可以推广到这类方程。

上面的讨论也可由这些方程所反映的物理现象来说明。波动方程所反映的波传播现象具有一定的传播速度，因而一点初始条件的影响范围是一圆锥体，一点的依赖区域也是圆锥体。由于热传导的现象进行得十分迅速，因而在方程中就近似地反映为无穷的传播速度，并表现成热传导方程的影响区域为无限的。至于拉普拉斯方程，它表示定常状态或平衡状态，这时不必考虑时间的因素，因而不产生影响的传播速度问题。

4）关于时间的反演

对时间的反演问题的物理意义，是考察相应物理状态的变化过程是否是可逆的。

一个物理状态，其变化过程为可逆的是指：设在某些外界条件下按某种规律变化的一物理状态，在时刻t1时处于状态A，到时刻t2时变为状态B，如果在t2时刻的状态B可以沿着相反的变化过程回复到原来的状态A，而使外界条件不发生其他的变化，那么我们就说这物理状态的变化过程是可逆的，否则，我们就说这物理状态的变化过程是不可逆的。

一物理状态的变化过程是否可逆在数学上反映为所归结出来的方程关于时间变量t是否是对称的，即以－t代替t后方程是否不变。(www.xing528.com)

在拉普拉斯方程中不出现时间变量，因而不会产生关于时间的反演问题。

波的传播是一个可逆过程。事实上，设以u（x，t）表示描写波的传播过程，它满足方程

在时刻t＝0，其物理状态为u（x，0）；而在时刻t＝t0时，其物理状态为u（x，t0）。如果要考察从t0时的状态u（x，t0）沿原来变化过程的逆向过程能否回复到t＝0时的状态u（x，0），只要在t≤t0时求解下面的定解问题：

并看它在0≤t≤t0时的状态是否与原来的状态u（x，t）相符合就行了。做变换t′＝t0－t，上面的问题就化为在t′≥0时求解

容易看出，这个问题的解就是

因此，波的传播状态从t′＝0（t＝t0）变化到t′＝t0（t＝0）的过程相当于u（x，t）从t＝t0变化到t＝0的过程，即是u（x，t）的逆变化过程。

对于热传导方程，情况就不一样。如以u（x，t）表示描写热传导过程的函数，它满足热传导方程

那么所满足的方程为

与原来的热传导方程不同。与此相应的是对热传导方程在区域t＜0内求解柯西问题通常是不适定的。在物理学中这是明显的，因为热传导方程所描述的物理现象如传导、扩散等都是由高到低、由密到稀的单向变化，这种变化过程是不可逆的。

5）解的渐近性态

波动方程和热传导方程都含有时间变量t。但是，在没有外力和阻尼的情形下，波动方程描述的是一个能量守恒的保守系统，而热传导方程描述的是热的传导或物质的扩散这样的耗散过程。源于如此不同的物理背景，当时间变量t趋于无穷时，解的渐近性态也有很大的不同。如在波动方程中所述，对在有界区间［0，l］上齐次第一类或第二类边界条件波动方程的初边值问题，其能量函数是守恒的，且从解的表达式也可见到，解表示为含有及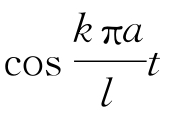的三角级数，故解并不衰减。而热传导方程初边值问题的解，是以指数衰减的方式趋于它的平衡态的。另外，无论是波动方程还是热传导方程，从解的渐近性态方面来说，初边值问题的解与初值问题的解也有很大不同。例如，对波动方程来说，齐次第一类或第二类边界条件初边值问题的解并不衰减，但是，对初值问题而言，在三维空间变量时，当初值是紧支集，t→∞时，解以t－1的衰减率趋于零。一般地，可以证明，在n个空间变量的情形，解及其偏导数会以的衰减率趋于零，即衰减率是和空间变量的维数n有关的。对热传导方程来说，初值问题和初边值问题之间的差别也很明显。对热传导方程齐次第一类或第二类边界条件的初边值问题，其解总以指数衰减率趋于它的平衡态，而对初值问题而言，解则以衰减率趋于零，其中n是空间变量的维数。这些性质对相应的非线性方程的研究是非常有用的。