调和方程描述的是稳态平衡的物理现象。以稳定的热传导为例,根据极值原理,温度的最高点及最低点在物体的边界上。对在边界上的温度最低点(温度最高点类似),物体其他各点的热量必流向它,并且通过它流向物体外部,因此边界处该点有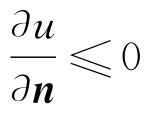 (n是外法线方向)。
(n是外法线方向)。
定理3.1(强极值原理) 设在半径为R的某一球上(包括球面在内)给定一个连续函数u(x,y,z),它在此球内是调和的,并且对此球的所有内点(x,y,z),成立着u(x,y,z)>u(x0,y0,z0),其中(x0,y0,z0)是球面上的某定点。如果函数u(x,y,z)在点(x0,y0,z0)沿方向ν的方向导数存在,而方向ν与球的内法线方向成锐角,则在点(x0,y0,z0)处成立
证明 由于调和函数在经过坐标轴的平移变换后仍然是调和函数,设球心为坐标原点。
由于u(x,y,z)在点(x0,y0,z0)取最小值,因此在点(x0,y0,z0)总有
取![]() ,则在(x0,y0,z0)点,函数ω应取其极小值0,且
,则在(x0,y0,z0)点,函数ω应取其极小值0,且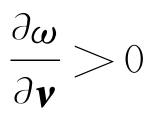 ,并在该点附近成立
,并在该点附近成立![]() 。取ω作变量r的函数
。取ω作变量r的函数![]() ,且满足以下三个条件:
,且满足以下三个条件:
(1)在球面R2=x2+y2+z2上ω=0;
(2)在同心球壳所围成的闭区域D: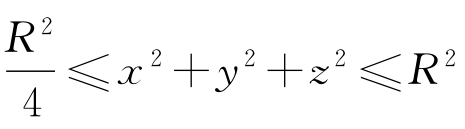 内,ω具有二阶连续偏导数,且Δω>0;
内,ω具有二阶连续偏导数,且Δω>0;
(3)ω沿球半径方向的导数![]() 存在,且r>0时
存在,且r>0时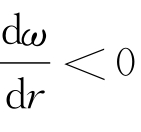 ,从而在球面R2=x2+y2+z2上
,从而在球面R2=x2+y2+z2上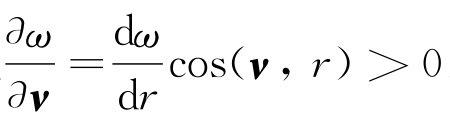 。
。
如果这样的函数ω(x,y,z)存在,则当ε>0足够小时,函数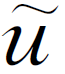 =εω+u(x0,y0,z0)就是我们所要找的函数。事实上,在(x0,y0,z0)点
=εω+u(x0,y0,z0)就是我们所要找的函数。事实上,在(x0,y0,z0)点
显然满足,我们只要证明当ε>0足够小时,在区域D上成立
m(x,y,z)=u-εω-u(x0,y0,z0)≥w(x0,y0,z0)=0(https://www.xing528.com)
由于在区域D中,Δm=-Δ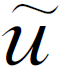 =-εΔω<0,因此函数ω在D内不能取到其最小值,但在区域D的边界上恒有m(x,y,z)≥0。这是由于在球面
=-εΔω<0,因此函数ω在D内不能取到其最小值,但在区域D的边界上恒有m(x,y,z)≥0。这是由于在球面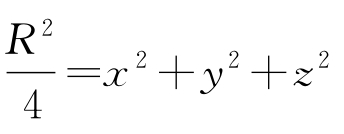 上,u(x,y,z)>u(x0,y0,z0),只要取ε>0足够小就可使在球面上m(x,y,z)=u-εωu(x0,y0,z0)>0;而在球面R2=x2+y2+z2显然有m(x,y,z)≥0。这样,在整个区域D上都有m(x,y,z)=u-εω-u(x0,y0,z0)≥m(x0,y0,z0)=0,这就是所要证明的。
上,u(x,y,z)>u(x0,y0,z0),只要取ε>0足够小就可使在球面上m(x,y,z)=u-εωu(x0,y0,z0)>0;而在球面R2=x2+y2+z2显然有m(x,y,z)≥0。这样,在整个区域D上都有m(x,y,z)=u-εω-u(x0,y0,z0)≥m(x0,y0,z0)=0,这就是所要证明的。
现在来证明上述函数ω(x,y,z)的确是存在的。
作函数![]() ,其中a是一个待定的正常数。我们要验证:当a适当大时,它就是满足上述要求的函数v。条件(1)和(3)显然满足,下面来验证条件(2)。v的二阶偏导数为
,其中a是一个待定的正常数。我们要验证:当a适当大时,它就是满足上述要求的函数v。条件(1)和(3)显然满足,下面来验证条件(2)。v的二阶偏导数为
因此
由于在D上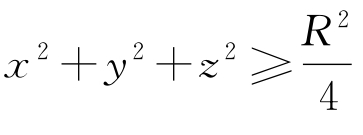 ,总可以取适当大的a>0,使在D内成立Δω>0,即条件(2)满足。定理证毕。
,总可以取适当大的a>0,使在D内成立Δω>0,即条件(2)满足。定理证毕。
由上述对于球的强极值原理,可以得到具有某种性质的一般区域的强极值原理。
定理3.2 设区域Ω具有下述性质:对Ω的边界Γ上任一点M,都可作一个属于区域Ω(连同其边界Γ)的球KM,使其在点M与Γ相切。如果不恒等于常数的调和函数u(x,y,z)在Ω∪Γ上连续,在边界点M0处取最小(最大)值,则只要它在点M0处关于Ω的外法向导数![]() 存在,其值必是负(正)的。
存在,其值必是负(正)的。
证明 取定一球KM0,并假设它的所有内点都属于Ω。由于调和函数u(x,y,z)不恒等于常数,根据极值原理,它不能在Ω的内点取到最小值,因此u(x,y,z)在KM0的所有内点上的值恒大于u在点M0的值。由定理3.1,只要导数![]() 存在,它在点M0处的值必是负的。
存在,它在点M0处的值必是负的。
在Γ上使函数u(x,y,z)取到最大值的那些点处,函数-u取到最小值,因此在这些点处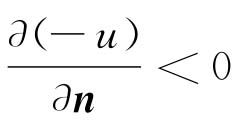 ,即
,即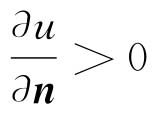 。定理证毕。
。定理证毕。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




