琴弦发声中的波动方程应用案例分析

利用受击乐器比如扬琴，可以弹奏出优美动听的乐曲，扬琴弦的两端固定，通过琴键可敲击其任一部位，受到敲击，整条弦便会产生自由振动，从而引起周围空气的振动，产生声波，但在演奏时必须用锤（平面锤或凸面锤）而决不可用细棒。

设琴弦长为l，以弦的一端为坐标原点，弦的初位置为x轴，弦上各点位移方向为u轴，被击点均在x＝x0处，如图2.15所示。

图2.15　琴弦振动示意图

1）平面锤敲击琴弦x＝x0点

假设锤的宽度为2d，则敲击区间实为（x0－d≤x≤x0＋d），由于是平面锤，因此在敲击瞬间该区间内各点获得相同的速度，设为g0，此后弦便开始自由振动，弦的振动归结为以下定解问题：

利用分离变换法，令u（x，t）＝X（x）·T（t），代入原方程

所以

（1）当λ＜0时，方程的解为

代入两个边界条件得

C1＝C2＝0

所以没有非零解。

（2）当λ＝0时，方程的解为

X（x）＝C1x＋C2

代入两个边界条件得

C1＝C2＝0

所以没有非零解。

（3）当λ＞0，方程的解为(www.xing528.com)

代入两个边界条件得C1＝0，为了使C2≠0，得，所以

将λk代入T″（t）＋a2λT（t）＝0，得

所以原方程的通解为

由傅里叶级数展开公式得

将Ak，Bk代入u（x，t）得

所以，弦的振动就是所有驻波的叠加，即n次谐波的幅度。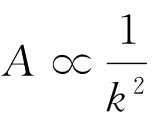

2）细棒敲击琴弦x＝x0点

设细棒给予x0点的冲量为I，弦线密度为ρ，取被击点x0处一无限小线元Δx，对线元应用动量定理得

ρΔxut（x，0）＝l

即

此后弦开始自由振动，弦的振动归结为以下定解问题：

再用一次分离变量法可得

其中

所以细棒敲击琴弦的振动方程的解为

此即弦的振动方程，弦的振动也是所有驻波的叠加，k次谐波叠加后幅度。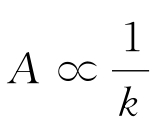

比较以上两种情况下弦的振动，可以看到由于初始条件不同，造成振动情况截然不同：当用平面锤敲击时，n次谐波的幅度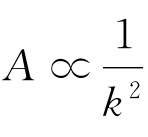，而用细棒敲击时，k次谐波的幅度A∝，由于相对于是k的更高阶无穷小，所以用平面锤时，声音的k次谐波随k的增加很快衰减掉了，振动包含较少的高次谐波（产生高次谐音），听起来比较悦耳；而用细棒的时候，乐器产生声音的k次谐波随k的增加衰减较慢，于是包含较多的高次谐波（产生高次谐音），听起来比较刺耳，所以演奏扬琴或其他受击乐器时，必须用锤而决不可用细棒。