波动方程在动力打桩中的应用

对桩的可打入性进行准确的分析和预测是打桩施工的关键环节，同时也关系到整个工程的进度与成败。近年来，在土木工程、海洋工程和港口工程中都出现了大直径、超长桩，这种桩的重量大，对桩的可打入性有显著影响。打桩分析的一维应力波动方程为

上式右边第二项为桩的自重对应力波传播的影响；第三项为桩周土体阻力对应力波传播的影响。

波动方程分为地表部分（不含地面阻力）与地底部分（两部分看成整体），即

1）对地表部分求解

由于在初始时刻之前，整个桩、土系统处于静止状态，t＝0时桩单元的弹簧力、土阻力、位移、速度及加速度均为零，以锤心的锤击初速度为已知边界条件，即得

将原方程分解为两个波动方程：

式中，。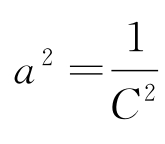

先解第一个方程。由齐次化原理，得到问题的解为

解第二个方程，注意到其为非齐次边界条件的情形，先令

U（x，t）＝C1（x－l）

再做变换

V（x，t）＝u（x，t）－U（x，t）

则V（x，t）满足方程

对该方程采用分离变量法，令

V（x，t）＝X（x）T（t）

XT″＝a2TX″

令

则有

T″＋λa2T＝0

X″＋λX＝0

考虑上式，根据边界条件X（x）应当满足边界条件

X′（0）＝0，X（2Δl）＝0(www.xing528.com)

讨论得：

（1）λ≤0时，只有平凡解X≡0。

（2）λ＞0时，

利用边界条件X′（0）＝0，得B＝0，于是由第二个边界条件得到

为使X（x）为非平凡解，λ应满足

于是

这样就找到了一组非零解

将固有值λk代入T满足的方程中，可得其通解为

于是得到一列可分离变量得特解

利用叠加原理构造级数形式的解

由V（x，0）＝V′（x，0）＝0，为使在t＝0时V（x，t）及V′（x，t）取到初值0，应成立

进行傅里叶正弦展开，有

得到

则原方程的解为

2）对地底部分求解

由于解析法将地表部分及地底部分各视作一个整体，则地表与地底交接处状态各为对方边界状态，由于t＝0时，桩处于静止状态，因此初始条件可知，边界条件由地表部分可知，则原方程可化为

（x＝2Δl相当于前一部分的x＝0）

式中，。

注意到其为非齐次方程，由齐次化原理，得到问题的解为

综上，1）、2）两种情况的解分别为