斜拉桥应用弦振动方程

斜拉桥是一种高次超静定结构，在设计斜拉桥时，通过计算其自重引起的恒载内力和受外力的变形状态来调整斜拉索的张拉力，从而达到施工阶段的理想状态。所以计算斜拉索的张力对斜拉桥结构的受力状态显得尤为重要。

基本假设：

（1）斜拉索的截面直径与其长度相比可以忽略不计，视为一根线密度为ρ的细线；

（2）忽略抗弯刚度的影响，简化为两端固定的无阻尼弦振动模型。

1）考虑无风载的情况

在斜拉索上任取一弦段（x1，x2）弧长为

忽略高阶小量，得弧长为Δx≈x2－x1。由于弦只在x轴的垂直方向做横振动，所以水平方向的合力为零（图2.13），即

图2.13　无风载斜拉索受力简图

T（x1）cosα－T（x2）cosβ＝0

因为弦只在平衡位置附近做微小振动，所以

cosα＝cosβ≈1

垂直方向上，考虑斜拉索的重力，有

根据动量定理，有

从而

得出该条件下的偏微分方程

由于斜拉索两端固定，处于张紧状态下，满足边界条件为

u（0，t）＝0，u（l，t）＝0

满足初值条件为

式中，l为斜拉索长；f1（x）为弦上任一点初始沿横向位移；f2（x）为弦上任一点初始横向速度。

首先求齐次方程

记。运用分离变量法，令

u（x，t）＝X（x）T（t）

代入并记等式值为－λ，得

由此

（1）当λ＜0时，

由边界条件得

解得只有平凡解X≡0，故舍去。

（2）当λ＝0时，

代入得C1＝C2＝0，只有平凡解X≡0，故舍去。(www.xing528.com)

（3）当λ＞0时，

代入得

于是

这样就求出一组非零解

将固有值λk代入T满足的方程，得

由叠加原理可得通解为

代入初值条件得

故齐次方程的形式解为

下面运用齐次化原理解非齐次方程

此时

Ak＝0

所以非齐次方程解为

2）考虑有风载的情况

对于有风载的情况，在海拔差不大的情况下，假设风载均匀分布，那么斜拉索上的干扰力可设为横向且均匀分布（图2.14）。令横向干扰力为Q（x，t），q（x，t）＝Q（x，t）/ρ，此时弦振动偏微分方程为

图2.14　有风载时斜拉索受力简图

弦上干扰力为风载，可用简谐函数［4］近似

式中，ρ1为气体密度；D为斜拉索直径；A为风载幅值；ω为风载频率；θ为风向与弦纵向间的夹角。

同理，方程

的解为

由此将斜拉索风载干扰力函数代入上式化简得

进一步化简得

其中

讨论风载频率ω：

若φ1，φ2中或φ3，φ4中，即

此时φ1，φ2趋于∞，或φ3，φ4趋于∞。

与斜拉索在无风载时的固有频率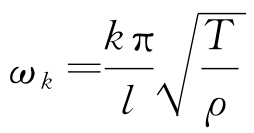相比较，当风载频率为上述情况时，可能发生共振现象，使斜拉索产生振幅较大的受迫振动。

综上所述，恒温条件下斜拉索两端为固定支承受风力影响下弦振动方程的解u（x，t）可由上述三解相加得到：

u（x，t）＝u1（x，t）＋u2（x，t）＋u3（x，t）