初边值问题解的唯一性与稳定性

本节讨论波动方程初边值问题

解的唯一性与稳定性。

1）初边值问题解的唯一性

根据薄膜振动的动能U和位能V的表示式，若不计一个常数因子，则薄膜的总能量可写成

其中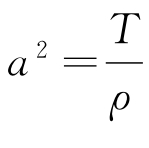。由于在没有外力的作用，对于薄膜振动的初边值问题

根据格林公式，可得

式（2.141）说明E（t）是一与时间t无关的常数，即E（t）≡E（0）。这也证明了能量守恒原理。对于初边值问题（2.138），设u1，u2是该定解问题的两个解，则u＝u1－u2满足相应的齐次方程及齐次边界条件，因此在初始时刻有E（0）＝0，故

即

ut＝ux＝uy＝0

又由于在初始时刻u＝0，故得

u（x，y，t）＝0

即

u1＝u2

唯一性得证。

定理2.3　波动方程初边值问题（2.138）的解如果存在的话，它一定是唯一的。

2）初边值问题解的稳定性

对于初边值问题（2.138），由于外力不等于零，根据式（2.141），可得

整理得(www.xing528.com)

再从0到t积分上式，得

即

于是对0≤t≤T，

其中C0＝eT，是一个仅与T有关的正常数。

进一步还可以得到函数u（x，y，t）本身平方模的估计。记

则

然后把e－t乘上式两端得

再从0到t积分上式，得到

即

结合式（2.144），对0≤t≤T，则

式中，C为一个只与T有关的正常数。式（2.144）或式（2.148）称为能量不等式或能量估计式，用来判断解对初始条件和右端项f的连续依赖性。这个估计式是在假设解存在的前提下得到的，具有这种特点的估计式均称为先验估计式。

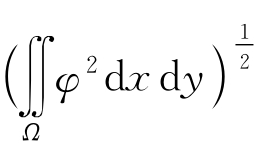对于定义在区域Ω上的函数φ和定义在区域（0，T）×Ω上的函数f，常以和分别表示和。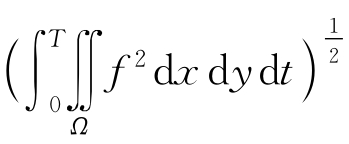

定理2.4　波动方程初边值问题（2.138）的解u（x，y，t）在下述意义下关于初始值（φ，φ）与方程右端项f是稳定的：对任何给定的ε＞0，一定可以找到仅依赖于ε和T的η＞0，只要

那么以（φ1，φ1）为初值、f1为右端项的解u1与以（φ2，φ2）为初值、f2为右端项的解u2之差在0≤t≤T上满足

证明　记v（x，y，t）＝u1（x，y，t）－u2（x，y，t），则v（x，y，t）满足

由能量不等式

式中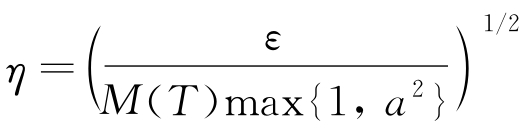，。稳定性得证。