泊松公式的物理意义及惠更斯原理

二维波动方程与三维波动方程的影响区域、依赖区域及决定区域有显著不同，这表明二维与三维波动的传播有实质的区别。

对于三维波动，（x0，y0，z0，0）的影响区域（2.131）表示一个以（x0，y0，z0）为中心、半径为at的球面，假设t＝0时在点中心（x0，y0，z0）有一瞬时扰动，随着时间的推移，扰动的影响面以速度a向四周扩大。对于空间一点（x1，y1，z1），假设它和中心（x0，y0，z0）的距离为r，则只有在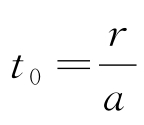的这一瞬时，此点才落在扰动面上（也就是说只有在此时刻此点才受到瞬时扰动的影响），过后又回复到未扰动前的状态。如果在点（x0，y0，z0）处的扰动持续进行了t1秒，则在点（x1，y1，z1）处所受扰动影响的时间也是t1秒，过后仍恢复到原来状态，只是其扰动开始比点（x0，y0，z0）迟t0秒而已。这种现象最典型的例子就是声音的传播，即从某个声源发出声音，经过一定时间后传到耳中，所听到声音的长短和发出的声音一样。

如果初始扰动为一有界区域Ω，该区域Ω中任一点M处的扰动，经时间t后，它传到以M为中心、以at为半径的球面上，因此在时刻t受到区域Ω中初始扰动影响的区域，就是所有以M∈Ω为中心、at为半径的球面的全体。当t足够大时，这种球面簇有内外两个包络面，外包络面称为传播波的前阵面，内包络面称为后阵面。这前、后阵面的中间部分就是受到扰动影响的部分。前阵面以外的部分表示扰动还未传到的区域，而后阵面以内的部分是波已传过并恢复了原来状态的区域。因此当初始扰动限制在空间某一局部范围内时，波的传播有清晰的前阵面和后阵面，这现象在物理学中称为惠更斯（Huygens）原理或无后效现象。它对信号的传送与接收具有重要的意义。

对于二维波动，点（x0，y0，0）影响区域（2.126）为锥体，在t＝0时刻点（x0，y0）处的瞬时扰动经过时间t后的影响范围不是圆周而是整个圆，随时间的推移，它以速度a不断向外扩大。对于与点（x0，y0）相距r的一点，经过后开始受到点（x0，y0）的扰动影响，但随着时间的增加，在此点的扰动影响并不消失，仍然继续发生作用。(www.xing528.com)

如果初始扰动在一个有界区域Ω中，对于区域Ω外的任一点M0（x0，y0），在t0时刻的状态为u（x0，y0，t0），假设d为M0到区域Ω的最近距离，则对于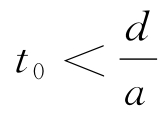的各时刻，函数u（M0，t0）＝0，即扰动的影响还未传到此点。从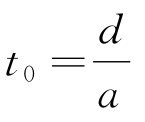开始，在点M0处开始受到扰动的影响，而且此扰动在以后不会消失。但随着t的推移，扰动的影响愈来愈弱。因此在二维情况，局部范围中的初始扰动具有长期连续的后效特性，波的传播有清晰的前阵面，但没有后阵面。这个现象称为波的弥散，或说这种波具有后效现象。

上述所讨论的波的传播现象并不仅限于二维与三维空间中的波动方程。可以证明，在空间维数n是奇数时（除n＝1外），对波动方程总成立前述的惠更斯原理；而当空间维数n是偶数时，总有波的弥散现象发生。